文章目录
树上搜索题目背景问题描述输入格式输出格式样例1输入样例1输出样例解释子任务 满分代码JavaC++Python
树上搜索
题目背景
西西艾弗岛大数据中心为了收集用于模型训练的数据，推出了一项自愿数据贡献的系统。岛上的居民可以登录该系统，回答系统提出的问题，从而为大数据中心提供数据。为了保证数据的质量，系统会评估回答的正确性，如果回答正确，系统会给予一定的奖励。
近期，大数据中心需要收集一批关于名词分类的数据。系统中会预先设置若干个名词类别，这些名词类别存在一定的层次关系。例如，“动物”是“生物”的次级类别，“鱼类”是“动物”的次级类别，“鸟类”是“动物”的次级类别，“鱼类”和“鸟类”是“动物”下的邻居类别。这些名词类别可以被按树形组织起来，即除了根类别外，每个类别都有且仅有一个上级类别。
并且所有的名词都可以被归类到某个类别中，即每个名词都有且仅有一个类别与其对应。一个类别的后代类别的定义是： 若该类别没有次级类别，则该类别没有后代类别；否则该类别的后代类别为该类别的所有次级类别，以及其所有次级类别的后代类别。
下图示意性地说明了标有星号的类别的次级类别和后代类别。
次级类别与后代类别
系统向用户提出问题的形式是：某名词是否属于某类别，而用户可以选择“是”或“否”来回答问题。该问题的含义是：某名词是否可以被归类到某类别或其后代类别中。
例如，要确定名词“鳕鱼”的类别，系统会向用户提出“鳕鱼是否属于动物”，当用户选择“是”时，系统会进一步询问“鳕鱼是否属于鱼类”，当用户选择“是”时，即可确定“鳕鱼”可以被归类到“鱼类”这一类别。
此外，如果没有更具体的分类，某一名词也可以被归类到非叶子结点的类别中。例如，要确定“猫”的类别，系统可以向用户提出“猫是否属于动物”，当用户选择“是”时，系统会进一步分别询问“猫”是否属于“鱼类”和“鸟类”，当两个问题收到了否定的答案后，系统会确定“猫”的类别是“动物”。
大数据中心根据此前的经验，已经知道了一个名词属于各个类别的可能性大小。为了用尽量少的问题确定某一名词的类别，大数据中心希望小 C 来设计一个方法，以减少系统向用户提出的问题的数量。
问题描述
小 C 观察了事先收集到的数据，并加以统计，得到了一个名词属于各个类别的可能性大小的信息。具体而言，每个类别都可以赋予一个被称为权重的值，值越大，说明一个名词属于该类别的可能性越大。由于每次向用户的询问可以获得两种回答，小 C 联想到了二分策略。他设计的策略如下：
对于每一个类别，统计它和其全部后代类别的权重之和，同时统计其余全部类别的权重之和，并求二者差值的绝对值，计为 w δ w_{\delta} wδ；选择 w δ w_{\delta} wδ 最小的类别，如果有多个，则选取编号最小的那一个，向用户询问名词是否属于该类别；如果用户回答“是”，则仅保留该类别及其后代类别，否则仅保留其余类别；重复步骤 1，直到只剩下一个类别，此时即可确定名词的类别。小 C 请你帮忙编写一个程序，来测试这个策略的有效性。你的程序首先读取到所有的类别及其上级次级关系，以及每个类别的权重。你的程序需要测试对于被归类到给定类别的名词，按照上述策略提问，向用户提出的所有问题。
输入格式
从标准输入读入数据。
输入的第一行包含空格分隔的两个正整数 n n n 和 m m m,分别表示全部类别的数量和需要测试的类别的数量。所有的类别从 1 到 n n n 编号，其中编号为 1 的是根类别。
输入的第二行包含 n n n 个空格分隔的正整数 w 1 , w 2 , … , w n w_1,w_2,\ldots,w_n w1,w2,…,wn，其中第 i i i 个数 w i w_i wi 表示编号为 i i i 的类别的权重。
输入的第三行包含 ( n − 1 ) (n-1) (n−1) 个空格分隔的正整数 p 2 , p 3 , … , p n p_2,p_3,\ldots,p_n p2,p3,…,pn，其中第 i i i 个数 p i + 1 p_{i+1} pi+1 表示编号为 ( i + 1 ) (i+1) (i+1) 的类别的上级类别的编号，其中 p i ∈ [ 1 , n ] p_i\in[1,n] pi∈[1,n]
接下来输入 m m m 行，每行一个正整数，表示带要测试的类别编号。
输出格式
输出 m m m 行，每行表示对一个被测试的类别的测试结果。表示按小 C 的询问策略，对属于给定的被测类别的名词，需要依次向用户提出的问题。
每行包含若干空格分隔的正整数，每个正整数表示一个问题中包含的类别的编号，按照提问的顺序输出。
样例1输入
5 210 50 10 10 201 1 3 353样例1输出
2 52 5 3 4样例解释
上述输入数据所表示的类别关系如下图所示，同时各个类别的权重也标注在了图上。
样例输入数据所表示的类别关系
对于归类于类别 5 的某个名词，按照上述询问策略，应当对于树上的每个节点，都计算 w δ w_{\delta} wδ 的值，对于类别 1 至 5，得到的 w δ w_{\delta} wδ 分别为：100、0、20、80、60。因此首先就类别 2 提问。由于类别 5 不属于类别 2 的后代类别，因此用户回答“否”，此时去除类别 2 和其全部后代类别，仅保留类别 1、3、4、5。对于剩下的类别，计算 w δ w_{\delta} wδ 的值，得到的 w δ w_{\delta} wδ 分别为：50、30、30、10。因此再就类别 5 提问。由于类别 5 就是被提问的名词所属类别，因此用户回答“是”，此时仅保留类别 5 和其全部后代类别。我们发现，这个时候，只剩下类别 5，因此算法结束。上述过程如下图所示：
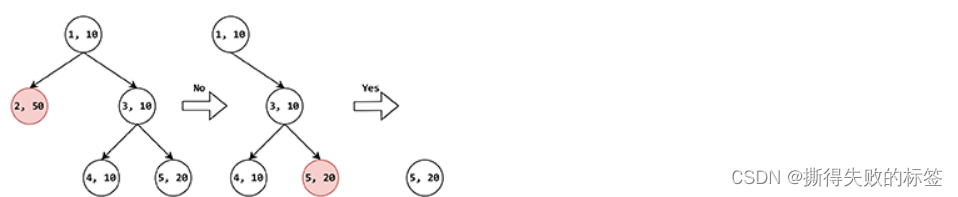算法执行过程 1
对于归类于类别 3 的某个名词，按照上述询问策略，依次对类别 2、5 提问，过程与前述一致。但是由于类别 3 不属于类别 2 的后代类别，用户回答“否”，此时应当去掉类别 5 和其后代类别，仅保留类别 1、3、4。分别计算 w δ w_{\delta} wδ 得：30、10、10。此时应当选择编号较小的类别 3 提问。由于类别 3 就是被提问的名词所属类别，因此用户回答“是”，此时仅保留类别 3 和其全部后代类别。我们发现，这个时候，并非只剩下一个类别，因此算法还应继续进行。剩下的类别有 3、4，分别计算 w δ w_{\delta} wδ 得：20、0。因此再就类别 4 提问。由于类别 3 不属于类别 4 的后代类别，用户回答“否”，此时应当去掉类别 4 和其后代类别，仅保留类别 3。我们发现，这个时候，只剩下类别 3，因此算法结束。上述过程如下图所示：
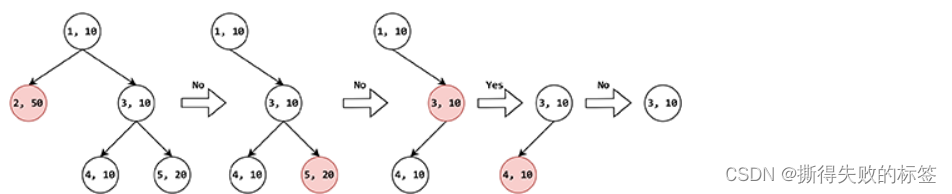
算法执行过程 2
子任务
对 20% 的数据，各个类别的权重相等，且每个类别的上级类别都是根类别；
对另外 20% 的数据，每个类别的权重相等，且每个类别至多有一个下级类别；
对 60% 的数据，有 n ≤ 100 n\leq100 n≤100,且 m ≤ 10 m\leq10 m≤10；
对 100% 的数据，有 n ≤ 2000 , m ≤ 100 n\leq2000,\quad m\leq100 n≤2000,m≤100, 且 w i ≤ 1 0 7 w_i\leq10^7 wi≤107。
满分代码
树结构的模拟题，这题直接深度优先暴力搜索就能过了，使用记忆化搜索应该能更快一点。
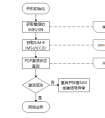
总体思路是：
通过深度优先搜索，将目标类别（从根类别 1 开始）的权重更新为其全部后代类别的权重之和；选择权值与其余全部可选的类别的权重之和的差最小的。如果有多个，则选取编号最小的那一个，输出该类别；通过深度优先搜索，判断是否属于该类别；如果属于，则仅保留该类别及其后代可选择的类别，将目标类别换成该类别否则保留其余类别，即删除该类别及其所有后代类别；重复上述步骤，逐步缩小搜索范围，直到只剩下一个类别，此时即可确定名词的类别。Java 和 C++ 的代码是满分，Python 代码只有 80 分，逻辑上是一样的还没找到那 20 分是哪里的错误
Java
import java.util.*;import java.io.*;public class Main { static long[] wi, temp; static List<Integer>[] ls; static Set<Integer> yes = new HashSet<>(); static Set<Integer> no = new HashSet<>(); public static void main(String[] args) throws IOException { QuickInput in = new QuickInput(); PrintWriter out = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out))); int n = in.nextInt(), m = in.nextInt(); temp = new long[n + 1]; ls = new List[n + 1]; for (int i = 1; i <= n; i++) temp[i] = in.nextInt(); for (int i = 1; i <= n; i++) ls[i] = new ArrayList<>(); for (int i = 2; i <= n; i++) ls[in.nextInt()].add(i); for (int i = 0; i < m; i++) { int t = in.nextInt(), pre = 1; no.clear(); while (true) { wi = Arrays.copyOf(temp, n + 1); yes.clear(); dfs(pre); if (yes.size() == 1) break; int idx = getMinIdx(pre); if (check(idx, t)) { pre = idx; } else { no.add(idx); } out.print(idx + " "); } out.println(); } out.flush(); } public static void dfs(int pre) { yes.add(pre); for (int i : ls[pre]) { if (!no.contains(i)) { dfs(i); wi[pre] += wi[i]; } } } public static int getMinIdx(int pre) { long min = Long.MAX_VALUE; int idx = 1; for (int j : yes) { long wj = Math.abs(wi[pre] - 2 * wi[j]); if (min > wj) { min = wj; idx = j; } } return idx; } public static boolean check(int idx, int t) { if (idx == t) return true; for (int i : ls[idx]) { if (no.contains(i)) continue; if (check(i, t)) return true; } return false; } static class QuickInput { StreamTokenizer input = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in))); int nextInt() throws IOException { input.nextToken(); return (int) input.nval; } }}C++
#include<bits/stdc++.h> using namespace std;vector<long long> wi, temp;vector<vector<int>> ls;set<int> yes, no;void dfs(int pre) { yes.insert(pre); for (int i : ls[pre]) { if (no.find(i) == no.end()) { dfs(i); wi[pre] += wi[i]; } }}int getMinIdx(int pre) { long long minDiff = LLONG_MAX; int idx = 1; for (int j : yes) { long long wj = abs(wi[pre] - 2 * wi[j]); if (minDiff > wj) { minDiff = wj; idx = j; } } return idx;}bool check(int idx, int t) { if (idx == t) return true; for (int i : ls[idx]) { if (no.find(i) != no.end()) continue; if (check(i, t)) return true; } return false;}int main() { ios::sync_with_stdio(false); cin.tie(0); int n, m; cin >> n >> m; temp.resize(n + 1); ls.resize(n + 1); for (int i = 1; i <= n; i++) cin >> temp[i]; for (int i = 1; i <= n; i++) ls[i] = vector<int>(); for (int i = 2; i <= n; i++) { int parent; cin >> parent; ls[parent].push_back(i); } for (int i = 0; i < m; i++) { int t, pre = 1; cin >> t; no.clear(); while (true) { wi = temp; yes.clear(); dfs(pre); if (yes.size() == 1) break; int idx = getMinIdx(pre); if (check(idx, t)) pre = idx; else no.insert(idx); cout << idx << " "; } cout << endl; } return 0;}Python
def dfs(pre): yes.add(pre) [dfs(i) for i in ls[pre] if i not in no] wi[pre] += sum(wi[i] for i in ls[pre] if i not in no)def check(idx, t): return idx == t or any(check(i, t) for i in ls[idx] if i not in no)n, m = map(int, input().split())temp = [0] + list(map(int, input().split()))ls = [[] for _ in range(n + 1)][ls[pa].append(i) for i, pa in enumerate(map(int, input().split()), 2)]for _ in range(m): t, pre, no = int(input()), 1, set() while True: wi, yes = temp.copy(), set() dfs(pre) if len(yes) == 1: break idx = min(yes, key=lambda j: abs(wi[pre] - 2 * wi[j])) if check(idx, t): pre = idx else: no.add(idx) print(idx, end=" ") print()
