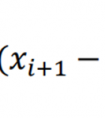
作者在前面的文章中介绍了两种经典的优化算法——遗传算法(GA)和粒子群算法(PSO),这些智能优化算法解决问题的方式和角度各不相同,都有各自的适用域和局限性,对智能优化算法自身做的改进在算法性能方面得到了一定程度的提升,但算法缺点的解决并不彻底。
为了克服使用单一智能优化算法在求解复杂问题中表现出的精度不高、易陷入局部最值、不能在全局搜索等一系列不足,算法融合的思想开始被研究和应用。因此本文将GA与PSO这两种经典算法进行融合,并辅以改进,从而利用它们的互补性,取长补短,提高求解复杂问题的能力。
00 文章目录
1 研究背景
2 遗传-粒子群自适应优化算法模型
3 代码目录
4 算法性能分析
5 源码获取
6 总结
01 研究背景
1.1 GA与PSO混合意义
无免费午餐定理,对任何优化问题,任两种优化算法的平均性能是相等的,没有任何一种优化算法在计算效率、通用性、全局搜索能力等性能方面都能表现得很好。
算法的混合也就成了算法优化领域的一个研究热点和趋势,混合有着固有的内在需求,不是简单地将算法组合叠加,要按照一定的策略和模式进行。
GA算法过程简单,全局收敛性好,多用于进行函数优化、数据挖掘、生产调度、组合优化、图像处理、机器学习等问题。但个体没有记忆,遗传操作盲目无方向,所需要的收敛时间长;
PSO算法原理简单,用速度、位移公式迭代易于实现,具有记忆功能,需要调节的参数少,在寻优稳定性和全局性收敛性方面具有很大优势,但容易陷入局部最优值出现早熟,种群多样性差,搜索范围小,在高维复杂问题寻优时更为明显,多用于求解组合优化、模式分解、传感器网络、生物分子研究等领域。
因此,GA算法因其遗传操作,种群多样,全局性好但个体没有记忆性,且收敛慢,而粒子群有记忆性,收敛快但易早熟,多样性差,这就使得两种算法在性能上有克服局限实现优势互补的可能,同时,作者在前面的文章中提出的自适应混沌粒子群能够使得初始解更加均匀,自适应变化的权重和学习因子能在一定程度上增加算法在进化后期搜索多样解的概率,因此将此改进引入混合模型中以期能提高算法性能。
1.2 遗传算法
遗传算法原理
1.3 自适应粒子群算法
自适应混沌粒子群
02 遗传-粒子群自适应优化算法模型
混合优化算法的方法有很多,有并行混合、串行混合、嵌入式混合三种,本文采用嵌入式混合。嵌入式混合是将整个算法或者是算法思想加入到另一个算法中,本文是将遗传算法的交叉与变异算子嵌入自适应混沌粒子群中,交叉与变异能够提高种群多样性并扩大算法的搜索范围,对算法取得全局最优解能够起到重要作用。
GA-APSO算法计算流程如下:

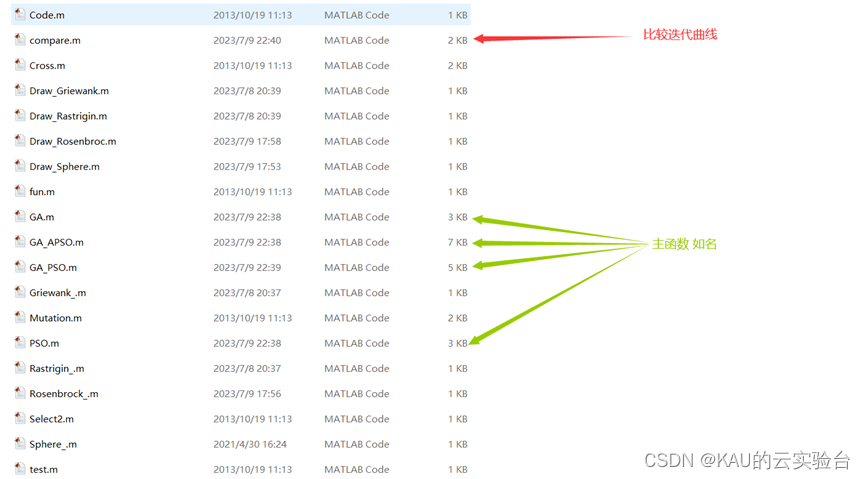
03 代码目录
04 算法性能分析
4.1 测试函数
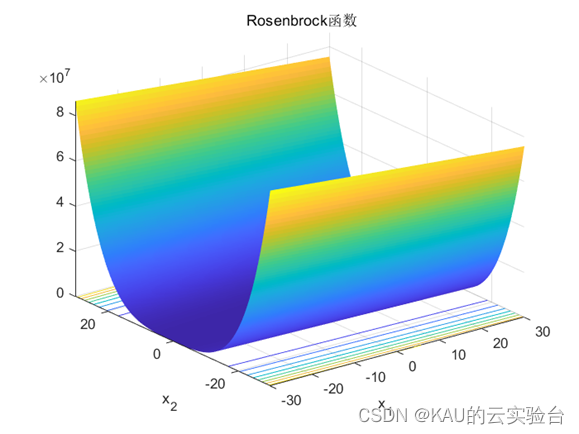
为了能够验证遗传-粒子群自适应算法对比本文提到的粒子群算法、遗传算法、遗传-粒子群算法有更好的效果,本文选用4个CEC的标准测试函数Sphere、Griewank、Rastrigin、Rosenbrock对算法的寻优精度、跳出局部能力、全局寻优能力进行检验。4个函数的表达式如下:
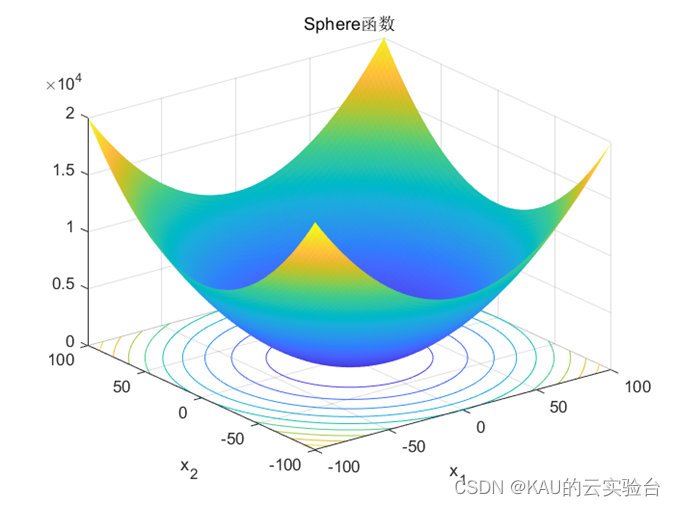
4.1.1 Sphere函数
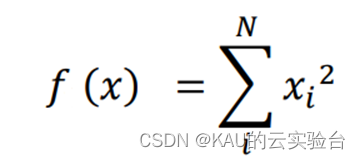
Sphere 函数的自变量𝑥𝑖的取值的范围:-100<𝑥𝑖<100;该函数存在唯一的一个全局的最小值,且当𝑥=(0,0,…,0)时,函数取得全局最小值 f1(x) = 0。选择该函数是对算法寻优的精度进行测试。
4.1.2 Griewank函数
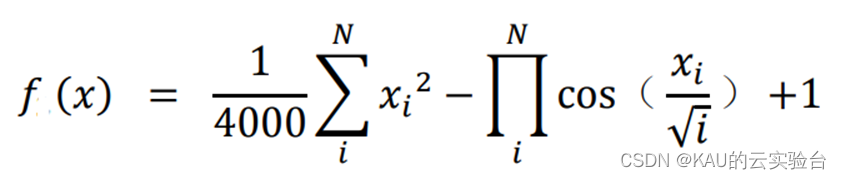
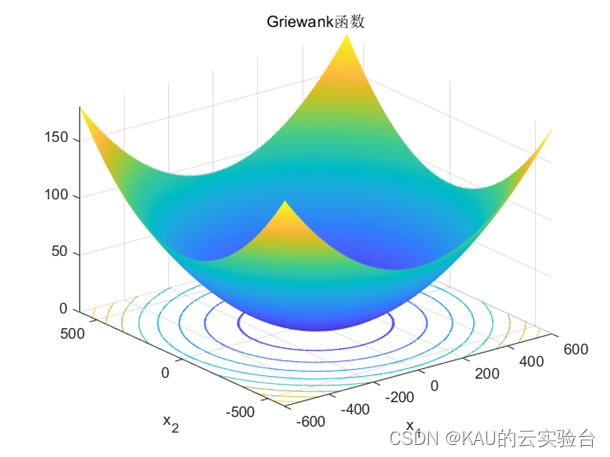
Griewank 函数的自变量𝑥𝑖的取值的范围:-600<𝑥𝑖<600;该函数在整个的数 据分布含有大量局部极值,但是存在全局最小值 f2(x) = 0,是一种比较复杂的多模的复杂性问题,因此选择该函数目的是对算法是否跳出局部,能够继续搜索的 能力进行测试。
4.1.3 Rastrigin函数
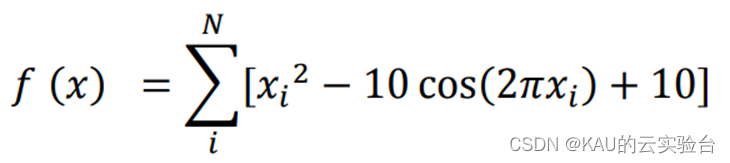
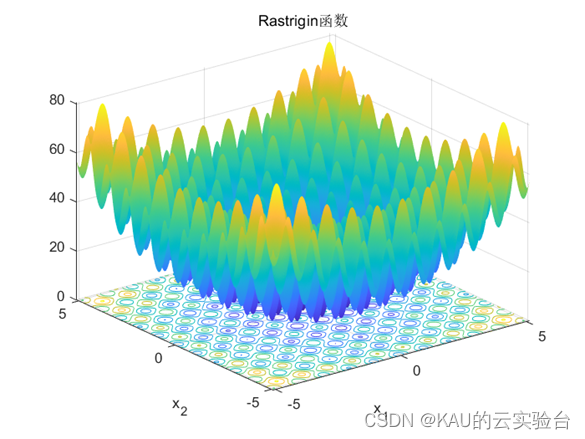
Rastrigin 函数的自变量𝑥𝑖的取值的范围:-5.12<𝑥𝑖<5.12;在 x = ( 0,0 ,…, 0 ) 处的时候存在全局极小点 0,该函数是一个非线性的多峰值函数,存在大量的局部最小值,寻找全局极小值时有一定的困难,因此用此函数可以,对算法的全局寻优能力检验测试。
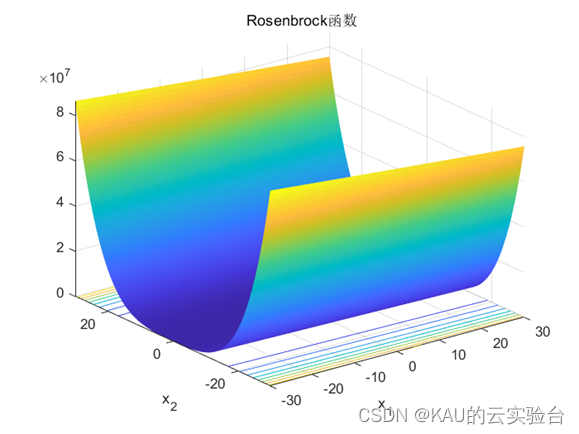
4.1.4 Rosenbrock函数
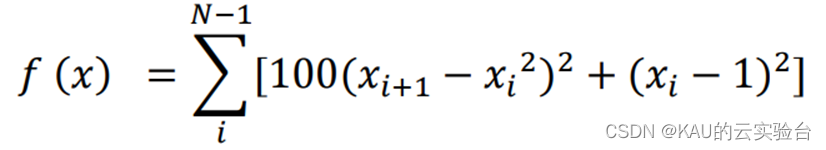
Rosenbrock 函数的自变量𝑥𝑖的取值的范围:-30<𝑥𝑖<30;该函数是一单峰函数, 存在全局极小值,位于一个类似开口向上的抛物线的最低点处,虽然能够比较容易找到,但是很难收敛到最低处,因此可以测试全局寻优的能力。
4.2 测试结果
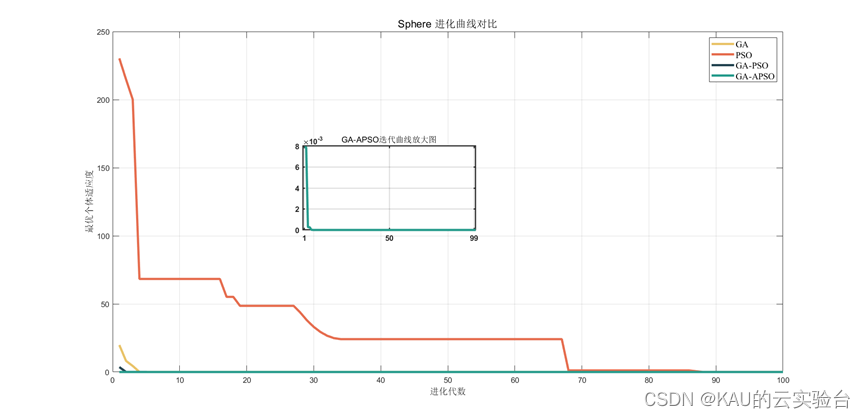
Sphere函数
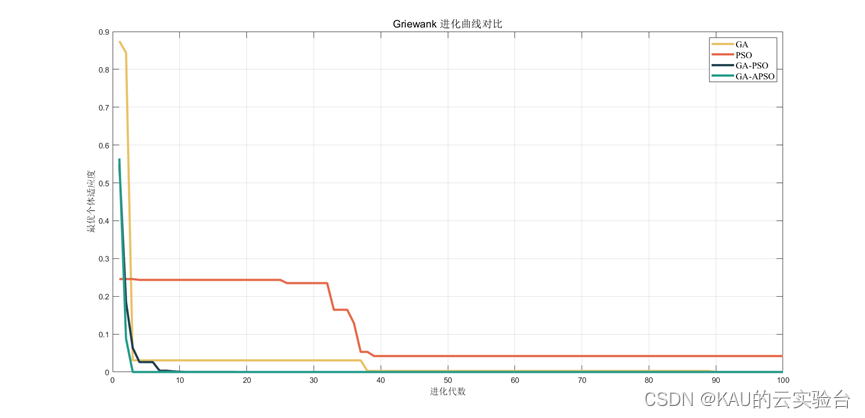
Griewank函数
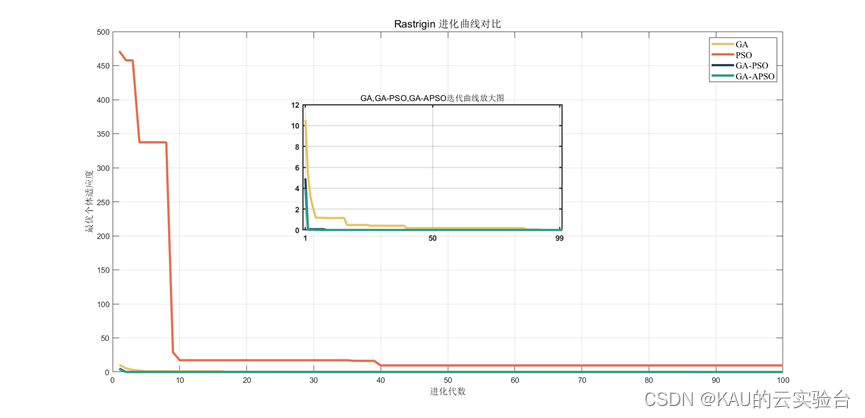
Rastrigin函数
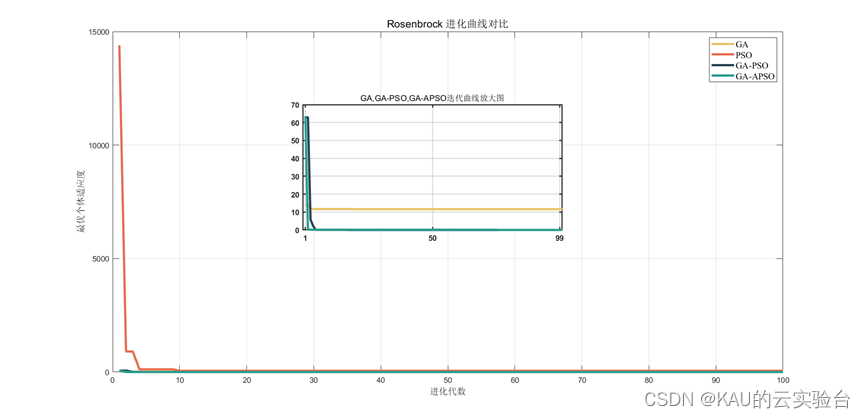
Rosenbrock函数
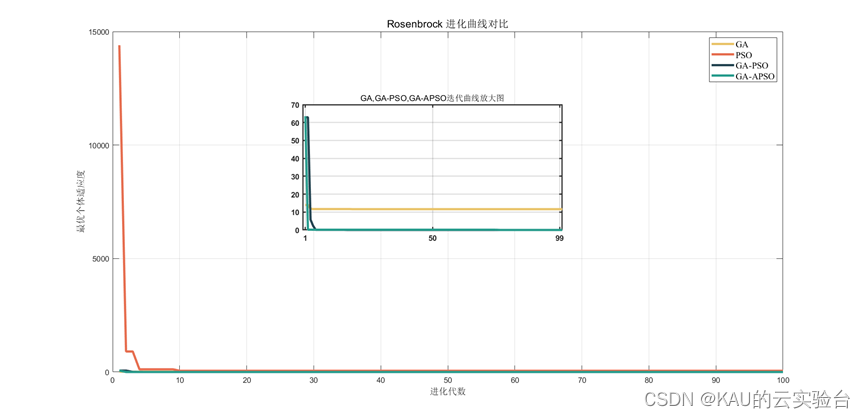
可以看到经遗传算法和粒子群算法经混合后能够极大的提升其全局寻优的性能,而经过改进后的粒子群与遗传算法进行混合仍能够在其基础上提升性能,因此此改进有效。
05 源码获取
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%https://mbd.pub/o/bread/ZJuVlpps%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%06 总结
本文中将遗传算法与自适应混沌粒子群算法进行混合寻优,对比GA-PSO,GA,PSO,其性能得到提升,同时也可以利用作者前面提到过的关于粒子群与遗传算法的多种改进方法进行混合,相信一定也能取得相当好的效果,后续作者也会更新关于混合算法的程序
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞 (ง •̀_•́)ง(不点也行),若有定制需求,可私信作者。