参考：
A橙_人工智能-实训平台
_南宫问天_HNU AI-----实验三：分类算法实验
灭绝星辰_人工智能实训 机器学习 朴素贝叶斯分类器
一．实验目的
掌握分类算法的算法思想：朴素贝叶斯算法，决策树算法，人工神经网络,支持向量机；编写朴素贝叶斯算法进行分类操作。二、实验平台
课程实训平台：课程实训平台
三、实验内容
机器学习 — 朴素贝叶斯分类器
四、实验步骤
1.第1关 条件概率；
（1）题一
P(AB)表示的是事件A与事件B同时发生的概率，P(A|B)表示的是事件B已经发生的条件下，事件A发生的概率。（2）题二
从1,2,...,15中小明和小红两人各任取一个数字，现已知小明取到的数字是5的倍数，请问小明取到的数大于小红取到的数的概率是多少？解：
设P(A)=小明取到的数字是5的倍数的概率；
P(B)=小明取到的数大于小红取到的数的概率；
（a）若小明小红可以取相同的数：
P （ B ∣ A ） = P ( A B ) P ( A ) P ( A ) = 3 / 15 P ( A B ) = P ( A 5 B ) + P ( A 10 B ) + P ( A 15 B ) = 1 15 ∗ 4 15 + 1 15 ∗ 9 15 + 1 15 ∗ 14 15 = 27 15 ∗ 15 P （ B ∣ A ） = 27 15 ∗ 15 3 15 = 27 3 ∗ 15 = 3 5 P（B|A）= \frac {P(AB)} {P(A)} \\ P(A)=3/15 \\ P(AB) = P(A_{5}B)+P(A_{10}B)+P(A_{15}B) \\ = \frac {1} {15} *\frac {4} {15}+\frac {1} {15} *\frac {9} {15}+\frac {1} {15} *\frac {14} {15} \\ = \frac {27} {15*15} \\ P（B|A）= \frac {\frac {27} {15*15} } {\frac {3} {15} }= \frac {27} {3*15}=\frac {3} {5} P（B∣A）=P(A)P(AB)P(A)=3/15P(AB)=P(A5B)+P(A10B)+P(A15B)=151∗154+151∗159+151∗1514=15∗1527P（B∣A）=15315∗1527=3∗1527=53
（b）若小明小红不能取相同的数：
P （ B ∣ A ） = P ( A B ) P ( A ) P ( A ) = 3 / 15 P ( A B ) = P ( A 5 B ) + P ( A 10 B ) + P ( A 15 B ) = 1 15 ∗ 4 14 + 1 15 ∗ 9 14 + 1 15 ∗ 14 14 = 27 15 ∗ 14 P （ B ∣ A ） = 27 15 ∗ 14 3 15 = 27 3 ∗ 14 = 9 14 P（B|A）= \frac {P(AB)} {P(A)} \\ P(A)=3/15 \\ P(AB) = P(A_{5}B)+P(A_{10}B)+P(A_{15}B) \\ = \frac {1} {15} *\frac {4} {14}+\frac {1} {15} *\frac {9} {14}+\frac {1} {15} *\frac {14} {14} \\ = \frac {27} {15*14} \\ P（B|A）= \frac {\frac {27} {15*14} } {\frac {3} {15} }= \frac {27} {3*14}=\frac {9} {14} P（B∣A）=P(A)P(AB)P(A)=3/15P(AB)=P(A5B)+P(A10B)+P(A15B)=151∗144+151∗149+151∗1414=15∗1427P（B∣A）=15315∗1427=3∗1427=149
2.第2关 贝叶斯公式；
（1）题一
对以往数据分析结果表明，当机器调整得良好时，产品的合格率为98%，而当机器发生某种故障时，产品的合格率为55%。每天早上机器开动时，机器调整得良好的概率为95%。计算已知某日早上第一件产品是合格时，机器调整得良好的概率是多少？解：
设良好-Good；故障-Fault；合格-Qualified；
已知：
求P（G | Q）：
P （ G ∣ Q ） = P （ Q ∣ G ） ∗ P （ G ） P （ Q ） = 0.98 ∗ 0.95 P ( G ) ∗ P （ Q ∣ G ） + P ( Q ) ∗ P （ Q ∣ F ） = 0.98 ∗ 0.95 0.95 ∗ 0.98 + 0.05 ∗ 0.55 = 0.931 / 0.9585 = 0.971309 P（G | Q）= \frac {P（Q | G）* P（G）} {P（ Q）} \\ = \frac {0.98*0.95} {P(G)*P（Q | G）+P(Q)*P（Q | F）} \\ = \frac {0.98*0.95} {0.95*0.98+0.05*0.55} \\ =0.931/0.9585= 0.971309 P（G∣Q）=P（Q）P（Q∣G）∗P（G）=P(G)∗P（Q∣G）+P(Q)∗P（Q∣F）0.98∗0.95=0.95∗0.98+0.05∗0.550.98∗0.95=0.931/0.9585=0.971309
（2）题二
一批产品共8件，其中正品6件，次品2件。现不放回地从中取产品两次，每次一件，求第二次取得正品的概率。解：
设 Q 1 1 为第一次取得正品， Q 1 0 为第一次取得次品； Q 2 1 为第二次取得正品； 设Q_{1}1为第一次取得正品，Q_{1}0为第一次取得次品；\\ Q_{2}1为第二次取得正品； 设Q11为第一次取得正品，Q10为第一次取得次品；Q21为第二次取得正品；
P ( Q 2 1 ) = s u m i = 0 1 P ( Q 1 i ) ∗ P ( Q 2 1 ∣ Q 1 i ) = P ( Q 1 0 ) ∗ P ( Q 2 1 ∣ Q 1 0 ) + P ( Q 1 1 ) ∗ P ( Q 2 1 ∣ Q 1 1 ) = 2 8 ∗ 6 7 + 6 8 ∗ 5 7 = 7 8 ∗ 6 7 = 3 4 P(Q_{2}1)=sum_{i=0} ^{1} P(Q_{1}i)*P(Q_{2}1|Q_{1}i) \\ = P(Q_{1}0)*P(Q_{2}1|Q_{1}0)+P(Q_{1}1)*P(Q_{2}1|Q_{1}1) \\ = \frac{2} {8} * \frac{6} {7} +\frac{6} {8} * \frac{5} {7} \\ = \frac{7} {8} * \frac{6} {7} = \frac{3} {4} P(Q21)=sumi=01P(Q1i)∗P(Q21∣Q1i)=P(Q10)∗P(Q21∣Q10)+P(Q11)∗P(Q21∣Q11)=82∗76+86∗75=87∗76=43
3.第3关 朴素贝叶斯分类算法流程；
（1）朴素贝叶斯算法
算法思想：根据特征预测结果 例如：特征：颜色B、声音C、纹理D；结果：好/坏瓜数学公式-（已知一个西瓜的三个特征，求其为好瓜A1的概率）P ( A 1 ∣ B C D ) = P ( A 1 ) P ( B ∣ A 1 ) P ( C ∣ A 1 ) P ( D ∣ A 1 ) P ( B C D ) P(A_{1}∣BCD)= \frac {P(A_{1})P(B∣A _{1} )P(C∣A _{1} )P(D∣A _{1})} {P(BCD)} P(A1∣BCD)=P(BCD)P(A1)P(B∣A1)P(C∣A1)P(D∣A1)
（2）fit-模型的训练
训练的流程（以西瓜为例）
计算各种条件概率：P(A1)、P(B∣A 1 )、P(C∣A 1 )、P(D∣A 1)等
参数说明-def fit(self, feature, label)
feature：训练集数据–颜色、声音、纹理，类型为ndarray；label：训练集标签–好/坏瓜，类型为ndarray；变量说明：
计算label_prob num：测试数据的个数cnt：好瓜的个数 计算condition_prob self.condition_prob[i][j][feat]：i：0-坏瓜；1-好瓜j：0-颜色、1-声音、2-纹理feat：1/2-绿/黄色、清脆/浑厚、清晰/模糊 计算条件概率： 每个特征取值除label为0、1的个数（num-cnt,cnt） def fit(self, feature, label): ''' 对模型进行训练，需要将各种概率分别保存在self.label_prob和self.condition_prob中 :param feature: 训练数据集所有特征组成的ndarray :param label:训练数据集中所有标签组成的ndarray :return: 无返回 ''' #********* Begin *********# #计算label_prob cnt = 0 num = 0 for item in label: num+=1 if item == 1: cnt+=1 self.label_prob[0] = (num-cnt)/num self.label_prob[1] = cnt/num #计算condition_prob self.condition_prob[0] = {} self.condition_prob[1] = {} #初始化每个特征取值的字典 for item in self.condition_prob: for feat in range(len(feature[0])): self.condition_prob[item][feat] = {} #记录每个特征的取值 i=0 #样本编号 for data in feature: j=0 #特征序号 for feat in data: if(self.condition_prob[0][j].get(feat)==None): self.condition_prob[0][j][feat] = 0 if(self.condition_prob[1][j].get(feat)==None): self.condition_prob[1][j][feat] = 0 if label[i]==0: self.condition_prob[0][j][feat] += 1 else: self.condition_prob[1][j][feat] += 1 j+=1 i+=1 #计算条件概率，每个特征取值除label为0和1的个数 for feat in range(len(feature[0])): for item in self.condition_prob[0][feat]: self.condition_prob[0][feat][item] /= (num-cnt) for item in self.condition_prob[1][feat]: self.condition_prob[1][feat][item] /= cnt #********* End *********#（3）predict-模型的预测
预测的流程（以西瓜为例）
根据朴素贝叶斯公式计算条件概率：
参数说明-def predict(self, feature)
feature：测试数据集所有特征组成的ndarray；return：模型预测结果–好/坏瓜，类型为ndarray；变量说明：
计算P（A1）、P（A2） P_good ：= self.label_prob[1]P_bad ：= self.label_prob[0] 计算P(B∣A1)、P(C∣A1)、P(D∣A1 ) P_good： *= self.condition_prob[1][feat_idx][feat]P_bad： *= self.condition_prob[0][feat_idx][feat]feat_idx+=1：以循环的形式，把B、C、D的条件概率都乘一下 判断好/坏瓜： if P_good>P_bad：取概率最大的类别作为预测结果 def predict(self, feature): ''' 对数据进行预测，返回预测结果 :param feature:测试数据集所有特征组成的ndarray :return: ''' # ********* Begin *********# res = [] for item in feature: P_good = self.label_prob[1] P_bad = self.label_prob[0] feat_idx = 0 for feat in item: P_good *= self.condition_prob[1][feat_idx][feat] P_bad *= self.condition_prob[0][feat_idx][feat] feat_idx+=1 if P_good>P_bad: res.append(1) else: res.append(0) return res #********* End *********#（4）完整代码
import numpy as np class NaiveBayesClassifier(object): def __init__(self): ''' self.label_prob表示每种类别在数据中出现的概率 例如，{0:0.333, 1:0.667}表示数据中类别0出现的概率为0.333，类别1的概率为0.667 ''' self.label_prob = {} ''' self.condition_prob表示每种类别确定的条件下各个特征出现的概率 例如训练数据集中的特征为 [[2, 1, 1], [1, 2, 2], [2, 2, 2], [2, 1, 2], [1, 2, 3]] 标签为[1, 0, 1, 0, 1] 那么当标签为0时第0列的值为1的概率为0.5，值为2的概率为0.5; 当标签为0时第1列的值为1的概率为0.5，值为2的概率为0.5; 当标签为0时第2列的值为1的概率为0，值为2的概率为1，值为3的概率为0; 当标签为1时第0列的值为1的概率为0.333，值为2的概率为0.666; 当标签为1时第1列的值为1的概率为0.333，值为2的概率为0.666; 当标签为1时第2列的值为1的概率为0.333，值为2的概率为0.333,值为3的概率为0.333; 因此self.label_prob的值如下： { 0:{ 0:{ 1:0.5 2:0.5 } 1:{ 1:0.5 2:0.5 } 2:{ 1:0 2:1 3:0 } } 1: { 0:{ 1:0.333 2:0.666 } 1:{ 1:0.333 2:0.666 } 2:{ 1:0.333 2:0.333 3:0.333 } } } ''' self.condition_prob = {} def fit(self, feature, label): ''' 对模型进行训练，需要将各种概率分别保存在self.label_prob和self.condition_prob中 :param feature: 训练数据集所有特征组成的ndarray :param label:训练数据集中所有标签组成的ndarray :return: 无返回 ''' #********* Begin *********# #计算label_prob cnt = 0 num = 0 for item in label: num+=1 if item == 1: cnt+=1 self.label_prob[0] = (num-cnt)/num self.label_prob[1] = cnt/num #计算condition_prob self.condition_prob[0] = {} self.condition_prob[1] = {} #初始化每个特征取值的字典 for item in self.condition_prob: for feat in range(len(feature[0])): self.condition_prob[item][feat] = {} #记录每个特征的取值 i=0 #样本编号 for data in feature: j=0 #特征序号 for feat in data: if(self.condition_prob[0][j].get(feat)==None): self.condition_prob[0][j][feat] = 0 if(self.condition_prob[1][j].get(feat)==None): self.condition_prob[1][j][feat] = 0 if label[i]==0: self.condition_prob[0][j][feat] += 1 else: self.condition_prob[1][j][feat] += 1 j+=1 i+=1 #计算条件概率，每个特征取值除label为0和1的个数 for feat in range(len(feature[0])): for item in self.condition_prob[0][feat]: self.condition_prob[0][feat][item] /= (num-cnt) for item in self.condition_prob[1][feat]: self.condition_prob[1][feat][item] /= cnt #********* End *********# def predict(self, feature): ''' 对数据进行预测，返回预测结果 :param feature:测试数据集所有特征组成的ndarray :return: ''' # ********* Begin *********# res = [] for item in feature: P_good = self.label_prob[1] P_bad = self.label_prob[0] feat_idx = 0 for feat in item: P_good *= self.condition_prob[1][feat_idx][feat] P_bad *= self.condition_prob[0][feat_idx][feat] feat_idx+=1 if P_good>P_bad: res.append(1) else: res.append(0) return res #********* End *********#4.第4关 拉普拉斯平滑；
（1）拉普拉斯平滑
为什么需要 拉普拉斯平滑：根据特征预测结果 举例：特征：颜色B、声音C、纹理D；结果：好/坏瓜下图中，坏瓜的纹理都是清晰，即P(模糊|否)=0–》得到的命题（模糊一定是坏瓜）并不合理；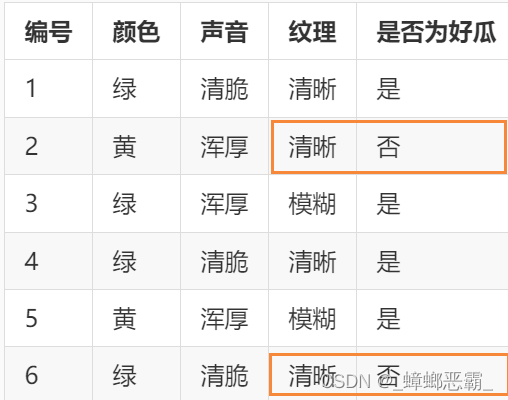
什么是拉普拉斯平滑 定义： N：训练集有多少种类别（好、坏–》2种）Ni：训练集中第i列有多少种取值（颜色、声音。纹理均各有2中取值）。训练过程中： 算类别的概率：分子加1，分母加N；算条件概率时：分子加1，分母加Ni 举例：经过拉普拉斯平滑后，P(模糊|否)=1/4，使得模型更加合理
（2）fit-模型的训练
训练的流程（以西瓜为例）参数说明-def fit(self, feature, label) feature：训练集数据–颜色、声音、纹理，类型为ndarray；label：训练集标签–好/坏瓜，类型为ndarray； 变量说明： 计算label_prob num：测试数据的个数cnt：好瓜的个数类别概率的平滑self.label_prob[0] = (num-cnt)+1/(num+types)：分子加1，分母加N（=2） 计算condition_prob self.condition_prob[i][j][feat]：i：0-坏瓜；1-好瓜j：0-颜色、1-声音、2-纹理feat：1/2-绿/黄色、清脆/浑厚、清晰/模糊条件概率的平滑（分子加一） self.condition_prob[0][j][feat] = 1：分子加一，初始化为1 计算条件概率： 条件概率的平滑（分母加Ni）每个特征取值除label为0、1的个数，再加Ni（num-cnt +len(self.condition_prob[0][feat]）,cnt +len(self.condition_prob[1][feat])）拉普拉斯平滑的定义：
- N：训练集有多少种类别（好、坏–》2种）
- Ni：训练集中第i列有多少种取值（颜色、声音。纹理均各有2中取值）。
- 训练过程中：
- 算类别的概率：分子加1，分母加N；
- 算条件概率时：分子加1，分母加Ni
def fit(self, feature, label): ''' 对模型进行训练，需要将各种概率分别保存在self.label_prob和self.condition_prob中 :param feature: 训练数据集所有特征组成的ndarray :param label:训练数据集中所有标签组成的ndarray :return: 无返回 ''' #********* Begin *********# #计算label_prob cnt = 0 num = 0 for item in label: num+=1 if item == 1: cnt+=1 types = 2 self.label_prob[0] = (num-cnt)+1/(num+types) self.label_prob[1] = cnt+1/(num+types) #计算condition_prob self.condition_prob[0] = {} self.condition_prob[1] = {} #初始化每个特征取值的字典 for item in self.condition_prob: for feat in range(len(feature[0])): self.condition_prob[item][feat] = {} #记录每个特征的取值 i=0 #样本编号 for data in feature: j=0 #特征序号 for feat in data: if(self.condition_prob[0][j].get(feat)==None): self.condition_prob[0][j][feat] = 1 #分子加一，初始化为1 if(self.condition_prob[1][j].get(feat)==None): self.condition_prob[1][j][feat] = 1 #分子加一，初始化为1 if label[i]==0: self.condition_prob[0][j][feat] += 1 else: self.condition_prob[1][j][feat] += 1 j+=1 i+=1 #计算条件概率，每个特征取值除label为0和1的个数 for feat in range(len(feature[0])): for item in self.condition_prob[0][feat]: self.condition_prob[0][feat][item] /= (num-cnt)+len(self.condition_prob[0][feat]) for item in self.condition_prob[1][feat]: self.condition_prob[1][feat][item] /= cnt+len(self.condition_prob[1][feat]) #********* End *********#（3）predict-模型的预测
预测的流程（以西瓜为例）
根据朴素贝叶斯公式计算条件概率： 不做修改直接用3.第3关 朴素贝叶斯分类算法流程的predict也行
而且3的predict比下面更容易看懂（可读性好）但下面的使用了一些函数，减少了一定的代码量 def predict(self, feature): ''' 对数据进行预测，返回预测结果 :param feature:测试数据集所有特征组成的ndarray :return: ''' result = [] # 对每条测试数据都进行预测 for i, f in enumerate(feature): # 可能的类别的概率 prob = np.zeros(len(self.label_prob.keys())) ii = 0 for label, label_prob in self.label_prob.items(): # 计算概率 prob[ii] = label_prob for j in range(len(feature[0])): prob[ii] *= self.condition_prob[label][j][f[j]] ii += 1 # 取概率最大的类别作为结果 result.append(list(self.label_prob.keys())[np.argmax(prob)]) return np.array(result)（4）完整代码
import numpy as np class NaiveBayesClassifier(object): def __init__(self): ''' self.label_prob表示每种类别在数据中出现的概率 例如，{0:0.333, 1:0.667}表示数据中类别0出现的概率为0.333，类别1的概率为0.667 ''' self.label_prob = {} ''' self.condition_prob表示每种类别确定的条件下各个特征出现的概率 例如训练数据集中的特征为 [[2, 1, 1], [1, 2, 2], [2, 2, 2], [2, 1, 2], [1, 2, 3]] 标签为[1, 0, 1, 0, 1] 那么当标签为0时第0列的值为1的概率为0.5，值为2的概率为0.5; 当标签为0时第1列的值为1的概率为0.5，值为2的概率为0.5; 当标签为0时第2列的值为1的概率为0，值为2的概率为1，值为3的概率为0; 当标签为1时第0列的值为1的概率为0.333，值为2的概率为0.666; 当标签为1时第1列的值为1的概率为0.333，值为2的概率为0.666; 当标签为1时第2列的值为1的概率为0.333，值为2的概率为0.333,值为3的概率为0.333; 因此self.label_prob的值如下： { 0:{ 0:{ 1:0.5 2:0.5 } 1:{ 1:0.5 2:0.5 } 2:{ 1:0 2:1 3:0 } } 1: { 0:{ 1:0.333 2:0.666 } 1:{ 1:0.333 2:0.666 } 2:{ 1:0.333 2:0.333 3:0.333 } } } ''' self.condition_prob = {} def fit(self, feature, label): ''' 对模型进行训练，需要将各种概率分别保存在self.label_prob和self.condition_prob中 :param feature: 训练数据集所有特征组成的ndarray :param label:训练数据集中所有标签组成的ndarray :return: 无返回 ''' #********* Begin *********# #计算label_prob cnt = 0 num = 0 for item in label: num+=1 if item == 1: cnt+=1 types = 2 self.label_prob[0] = (num-cnt)+1/(num+types) self.label_prob[1] = cnt+1/(num+types) #计算condition_prob self.condition_prob[0] = {} self.condition_prob[1] = {} #初始化每个特征取值的字典 for item in self.condition_prob: for feat in range(len(feature[0])): self.condition_prob[item][feat] = {} #记录每个特征的取值 i=0 #样本编号 for data in feature: j=0 #特征序号 for feat in data: if(self.condition_prob[0][j].get(feat)==None): self.condition_prob[0][j][feat] = 1 #分子加一，初始化为1 if(self.condition_prob[1][j].get(feat)==None): self.condition_prob[1][j][feat] = 1 #分子加一，初始化为1 if label[i]==0: self.condition_prob[0][j][feat] += 1 else: self.condition_prob[1][j][feat] += 1 j+=1 i+=1 #计算条件概率，每个特征取值除label为0和1的个数 for feat in range(len(feature[0])): for item in self.condition_prob[0][feat]: self.condition_prob[0][feat][item] /= (num-cnt)+len(self.condition_prob[0][feat]) for item in self.condition_prob[1][feat]: self.condition_prob[1][feat][item] /= cnt+len(self.condition_prob[1][feat]) #********* End *********# def predict(self, feature): ''' 对数据进行预测，返回预测结果 :param feature:测试数据集所有特征组成的ndarray :return: ''' result = [] # 对每条测试数据都进行预测 for i, f in enumerate(feature): # 可能的类别的概率 prob = np.zeros(len(self.label_prob.keys())) ii = 0 for label, label_prob in self.label_prob.items(): # 计算概率 prob[ii] = label_prob for j in range(len(feature[0])): prob[ii] *= self.condition_prob[label][j][f[j]] ii += 1 # 取概率最大的类别作为结果 result.append(list(self.label_prob.keys())[np.argmax(prob)]) return np.array(result)5.第5关 新闻文本主题分类
（1）新闻文本主题分类的三个步骤
词频向量化：sklearn中的CountVectorizer类 将字符串转换成向量;举例：I have a apple！ I have a pen!转换为[10, 7, 0, 1, 2, 6, 22, 100, 8, 0, 1, 0]。from sklearn.feature_ext\fraction.text import CountVectorizer#实例化向量化对象vec = CountVectorizer()#将训练集中的新闻向量化X_train = vec.fit_transform(X_train)#将测试集中的新闻向量化X_test = vec.transform(X_test)from sklearn.feature_ext\fraction.text import TfidfTransformer#实例化tf-idf对象tfidf = TfidfTransformer()#将训练集中的词频向量用tf-idf进行转换X_train = tfidf.fit_transform(X_train_count_vectorizer)#将测试集中的词频向量用tf-idf进行转换X_test = vec.transform(X_test_count_vectorizer)from sklearn.naive_bayes import MultinomialNBclf = MultinomialNB()clf.fit(X_train, Y_train)result = clf.predict(X_test)（2）news_predict-新闻文本主题分类
参数说明-def news_predict(train_sample, train_label, train_sample：原始训练样本，类型为ndarraytrain_label：训练标签，类型为ndarraytest_sample：原始测试样本，类型为ndarray 实现： 这里的实现其实就是：把上面三个部分的代码（词频向量化-CountVectorizer、构建文本向量-tf-idf、构建文本向量-MultinomialNB）简单合并在一起def news_predict(train_sample, train_label, test_sample): ''' 训练模型并进行预测，返回预测结果 :param train_sample:原始训练集中的新闻文本，类型为ndarray :param train_label:训练集中新闻文本对应的主题标签，类型为ndarray :param test_sample:原始测试集中的新闻文本，类型为ndarray :return 预测结果，类型为ndarray ''' #********* Begin *********# vec = CountVectorizer() train_sample = vec.fit_transform(train_sample) test_sample = vec.transform(test_sample) tfidf = TfidfTransformer() train_sample = tfidf.fit_transform(train_sample) test_sample = tfidf.transform(test_sample) mnb = MultinomialNB(alpha=0.02) mnb.fit(train_sample,train_label) predict = mnb.predict(test_sample) return predict #********* End *********#（3）完整代码
from sklearn.feature_extraction.text import CountVectorizerfrom sklearn.naive_bayes import MultinomialNBfrom sklearn.feature_extraction.text import TfidfTransformerdef news_predict(train_sample, train_label, test_sample): ''' 训练模型并进行预测，返回预测结果 :param train_sample:原始训练集中的新闻文本，类型为ndarray :param train_label:训练集中新闻文本对应的主题标签，类型为ndarray :param test_sample:原始测试集中的新闻文本，类型为ndarray :return 预测结果，类型为ndarray ''' #********* Begin *********# vec = CountVectorizer() train_sample = vec.fit_transform(train_sample) test_sample = vec.transform(test_sample) tfidf = TfidfTransformer() train_sample = tfidf.fit_transform(train_sample) test_sample = tfidf.transform(test_sample) mnb = MultinomialNB(alpha=0.02) mnb.fit(train_sample,train_label) predict = mnb.predict(test_sample) return predict #********* End *********#
