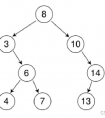
前言:这篇文章我们将分享一种新的数据结构类型——二叉搜索树。
目录
一、什么是二叉搜索树
二、定义
三、操作
1.插入
2.遍历
3.寻找
4.删除
四.完整代码
总结
一、什么是二叉搜索树
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值若它的右子树不为空,则右子树上所有节点的值都大于根节点的值它的左右子树也分别为二叉搜索树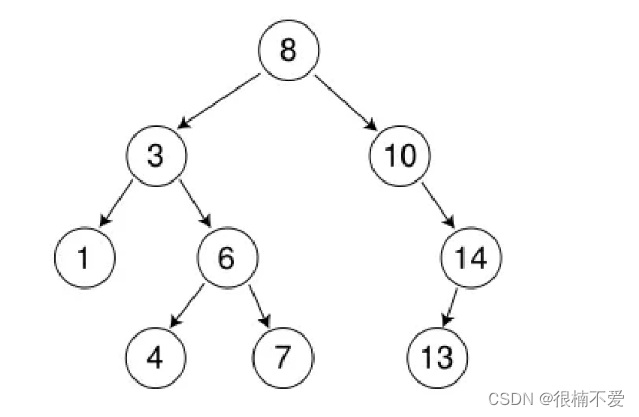
下面我们就来看看二叉搜索树的结构,及其提供的各种操作。
之所以能被称为二叉排序树,是因为其中序遍历的结果是树中所有节点值的升序序列。
二、定义
template<class K>struct BSTreeNode{K _val;struct BSTreeNode<K>* _left;struct BSTreeNode<K>* _right;BSTreeNode(const K& key):_left(nullptr),_right(nullptr),_key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public:private:Node* _root = nullptr;};整体的定义结构与C语言定义的二叉树一致,只是这里使用的是C++类定义。
三、操作
1.插入
插入,我们首先要考虑的就是空树的判断。
其次要注意,由于二叉搜索树是一个有顺序的树,所以我们就需要按照二叉搜索树的规则与每个节点的值进行比较不断往下走至叶子结点,最后成为新的叶子结点:
bool Insert(const K& val){if (_root == nullptr){_root = new Node(val);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_val < val){parent = cur;cur = cur->_right;}else if (cur->_val > val){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(val);if (val < parent->_val){parent->_left = cur;}else{parent->_right = cur;}return true;}在定义cur遍历比较的同时,我们还需要定义一个parent来记录最后新节点要插入的父节点。
由于二叉搜索树要起到搜索的作用,所以不允许存在元素相同的节点,所以我们要规避插入已有元素的情况。
2.遍历
遍历二叉树搜索树,直接采用中序遍历的方法:
void inOrder(const Node* root){if (root == nullptr){return;}inOrder(root->_left);cout << root->_val << " ";inOrder(root->_right);}这里有一个小问题,如果该函数定义在public下,由于要传参数root,而root又是private私有成员,所以我们无法在类外调用私有成员进行参数的传递,所以优化一下:
void InOrder(){inOrder(_root);}void inOrder(const Node* root){if (root == nullptr){return;}inOrder(root->_left);cout << root->_val << " ";inOrder(root->_right);}重新定义一个public成员函数InOrder,并将用该函数作为桥梁去调用inOrder,就可以避免传参。
测试如下:
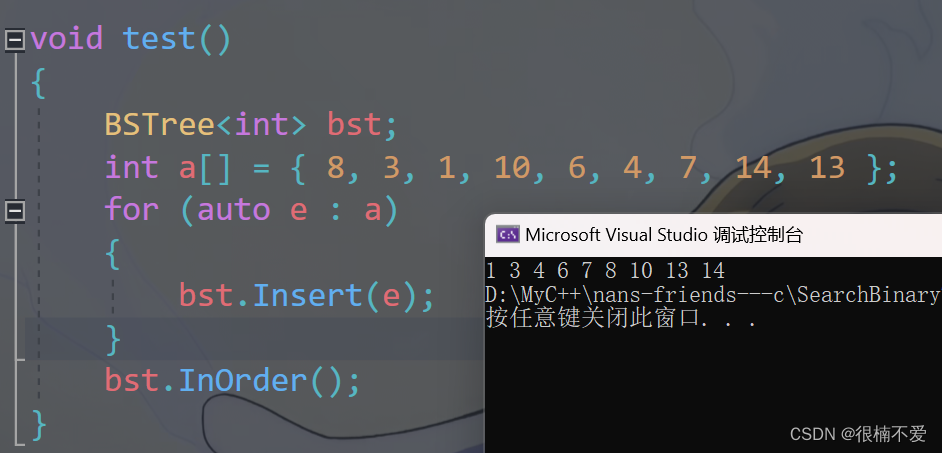
3.寻找
寻找其实就和插入类似,按照大小比较去遍历寻找:
bool Find(const K& val){if (_root == nullptr){return false;}Node* cur = _root;while (cur){if (cur->_val < val){cur = cur->_right;}else if (cur->_val > val){cur = cur->_left;}else{return true;}}return false;}4.删除
删除这个操作,可以说是二叉搜索树底层最复杂的一个操作,下面我们就通过下图来进行分析:

关于节点的删除,我们要分析四种情况:
1.如果说我们要删除1、4、7、13这样的叶节点,那就非常方便,只用找到它,再记录它的父节点,将它删除后,再让父节点原本指向它的指针指向nullptr即可。
2.如果是10、14这样的只有一个子节点的节点,我们只需让它的父节点去指向它的子节点即可,唯一要注意的是你是父节点的哪边的子节点,就让你的子节点成为哪边的子节点。
3.如果是3、6这样的用有两个字节点的节点,如果把它删除,无法让它的父节点同时指向两个子节点,所以就必须找到另一个节点来顶替它的位置,否则就破坏了二叉搜索树的规则。
那么这个顶替的节点应该是谁呢,要知道,这个新节点必须要比左子节点大,比右子节点小,那么我们就只有两种选择,一个是左子树的最大节点,一个是右子树的最小节点。
这两个节点选择哪一个都可以,这里我们以选择右子树的最小节点为例。
下面我们来一步步分析(代码不全仅供参考):
首先我们仍然是要通过循环遍历去找到要删除的节点,找不到则返回false。
Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_val < val){parent = cur;cur = cur->_right;}else if (cur->_val > val){parent = cur;cur = cur->_left;}其中叶节点的删除是可以和单子节点的删除混合的,来看:
//左为空,父节点指向我的右节点if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}//右为空,父节点指向我的左节点else if(cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;因为叶节点的左右子节点都为空,所以会默认进入if条件进行删除。
这里也比较简单,让cur的父节点原本指向它的指针转而去指向它的子节点。
值得注意的是如果要删除的是根节点, 那么就直接让根的单子节点成为新根即可。
最后来看拥有双子节点的cur如何删除:
//左右都不为空,替换法删除//寻找右子树的最左节点删除Node* rightMinParent = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinParent = rightMin;rightMin = rightMin->_left;}swap(cur->_val, rightMin->_val);if (rightMinParent->_left == rightMin){rightMinParent->_left = rightMin->_right;}else{rightMinParent->_right = rightMin->_right;}delete rightMin;思路为:找到cur的右子树的最小节点,将两者的数值交换,再去删除该最小节点。
首先我们需要定义cur的右子树的最小节点,及其父节点,然后去循环遍历找到二者,交换之后,再按照删除叶节点的方式删除该最小节点即可。
测试如下:

删除后我们的顺序并没有变化,说明我们的代码完全正确。
四.完整代码
template<class K>struct BSTreeNode{K _val;struct BSTreeNode<K>* _left;struct BSTreeNode<K>* _right;BSTreeNode(const K& val):_left(nullptr),_right(nullptr),_val(val){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public://插入bool Insert(const K& val){if (_root == nullptr){_root = new Node(val);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_val < val){parent = cur;cur = cur->_right;}else if (cur->_val > val){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(val);if (val < parent->_val){parent->_left = cur;}else{parent->_right = cur;}return true;}//寻找bool Find(const K& val){if (_root == nullptr){return false;}Node* cur = _root;while (cur){if (cur->_val < val){cur = cur->_right;}else if (cur->_val > val){cur = cur->_left;}else{return true;}}return false;}//删除bool erase(const K& val){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_val < val){parent = cur;cur = cur->_right;}else if (cur->_val > val){parent = cur;cur = cur->_left;}else{//左为空,父节点指向我的右节点if (cur->_left == nullptr){if (cur == _root){_root = cur->_right;}else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}delete cur;}//右为空,父节点指向我的左节点else if(cur->_right == nullptr){if (cur == _root){_root = cur->_left;}else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else{//左右都不为空,替换法删除//寻找右子树的最左节点删除Node* rightMinParent = cur;Node* rightMin = cur->_right;while (rightMin->_left){rightMinParent = rightMin;rightMin = rightMin->_left;}swap(cur->_val, rightMin->_val);if (rightMinParent->_left == rightMin){rightMinParent->_left = rightMin->_right;}else{rightMinParent->_right = rightMin->_right;}delete rightMin;}}}return false;}//遍历void InOrder(){inOrder(_root);cout << endl;}void inOrder(const Node* root){if (root == nullptr){return;}inOrder(root->_left);cout << root->_val << " ";inOrder(root->_right);}private:Node* _root = nullptr;};总结
关于二叉搜索树的简单知识就分享到这里,喜欢本篇文章记得一键三连,我们下期再见。