文章目录
发现宝藏【考生须知】试题 A: 裁纸刀试题 B: 寻找整数试题 C : \mathrm{C}: C: 求和试题 D: GCD试题 E: 蜂巢试题 F : \mathrm{F}: F: 全排列的价值试题 G: 青蛙过河试题 H \mathrm{H} H : 因数平方和试题 I: 最优清零方案试题 J : \mathrm{J}: J: 推导部分和
发现宝藏
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【宝藏入口】。
【考生须知】
考试开始后, 选手首先下载题目, 并使用考场现场公布的解压密码解压试题。
考试时间为 4 小时。考试期间选手可浏览自己已经提交的答案, 被浏览的答案允许拷贝。时间截止后,将无法继续提交或浏览答案。
对同一题目, 选手可多次提交答案, 以最后一次提交的答案为准。
选手必须通过浏览器方式提交自己的答案。选手在其它位置的作答或其它方式提交的答案无效。
试题包含 “结果填空” 和 “程序设计” 两种题型。
结果填空题: 要求选手根据题目描述直接填写结果。求解方式不限。不要求源代码。把结果填空的答案直接通过网页提交即可, 不要书写多余的内容。
程序设计题: 要求选手设计的程序对于给定的输入能给出正确的输出结果。考生的程序只有能运行出正确结果才有机会得分。
注意: 在评卷时使用的输入数据与试卷中给出的示例数据可能是不同的。选手的程序必须是通用的, 不能只对试卷中给定的数据有效。
所有源码必须在同一文件中。调试通过后,拷贝提交。
注意: 不要使用 package 语句。
注意:选手代码的主类名必须为: Main, 否则会被判为无效代码。
注意: 如果程序中引用了类库, 在提交时必须将 import 语句与程序的其他部分同时提交。只允许使用 Java 自带的类库。
试题 A: 裁纸刀
本题总分: 5 分
【问题描述】
小蓝有一个裁纸刀, 每次可以将一张纸沿一条直线裁成两半。
小蓝用一张纸打印出两行三列共 6 个二维码, 至少使用九次截出来, 下图给出了一种裁法。

在上面的例子中, 小蓝的打印机没办法打印到边缘, 所以边缘至少要裁 4 次。另外, 小蓝每次只能截一张纸, 不能重叠或者拼起来栽。
如果小蓝要用一张纸打印出 20 行 22 列共 440 个二维码, 他至少需要截多少次?
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 B: 寻找整数
本题总分: 5 分
【问题描述】
有一个不超过 1 0 17 10^{17} 1017 的正整数 n n n, 知道这个数除以 2 至 49 后的余数如下表所示, 求这个正整数最小是多少。
| a a a | n m o d a n \bmod a nmoda | a a a | n m o d a n \bmod a nmoda | a a a | n m o d a n \bmod a nmoda | a a a | n m o d a n \bmod a nmoda |
|---|---|---|---|---|---|---|---|
| 2 | 1 | 14 | 11 | 26 | 23 | 38 | 37 |
| 3 | 2 | 15 | 14 | 27 | 20 | 39 | 23 |
| 4 | 1 | 16 | 9 | 28 | 25 | 40 | 9 |
| 5 | 4 | 17 | 0 | 29 | 16 | 41 | 1 |
| 6 | 5 | 18 | 11 | 30 | 29 | 42 | 11 |
| 7 | 4 | 19 | 18 | 31 | 27 | 43 | 11 |
| 8 | 1 | 20 | 9 | 32 | 25 | 44 | 33 |
| 9 | 2 | 21 | 11 | 33 | 11 | 45 | 29 |
| 10 | 9 | 22 | 11 | 34 | 17 | 46 | 15 |
| 11 | 0 | 23 | 15 | 35 | 4 | 47 | 5 |
| 12 | 5 | 24 | 17 | 36 | 29 | 48 | 41 |
| 13 | 10 | 25 | 9 | 37 | 22 | 49 | 46 |
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 C : \mathrm{C}: C: 求和
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB
本题总分:10 分
【问题描述】
给定 n n n 个整数 a 1 , a 2 , ⋯ , a n a_{1}, a_{2}, \cdots, a_{n} a1,a2,⋯,an, 求它们两两相乘再相加的和, 即
S = a 1 ⋅ a 2 + a 1 ⋅ a 3 + ⋯ + a 1 ⋅ a n + a 2 ⋅ a 3 + ⋯ + a n − 2 ⋅ a n − 1 + a n − 2 ⋅ a n + a n − 1 ⋅ a n ⋅ S=a_{1} \cdot a_{2}+a_{1} \cdot a_{3}+\cdots+a_{1} \cdot a_{n}+a_{2} \cdot a_{3}+\cdots+a_{n-2} \cdot a_{n-1}+a_{n-2} \cdot a_{n}+a_{n-1} \cdot a_{n} \cdot S=a1⋅a2+a1⋅a3+⋯+a1⋅an+a2⋅a3+⋯+an−2⋅an−1+an−2⋅an+an−1⋅an⋅
【输入格式】
输入的第一行包含一个整数 n n n 。
第二行包含 n n n 个整数 a 1 , a 2 , ⋯ a n a_{1}, a_{2}, \cdots a_{n} a1,a2,⋯an 。
【输出格式】
输出一个整数 S S S, 表示所求的和。请使用合适的数据类型进行运算。
【样例输入】
4 \begin{array}{llll}4\end{array} 4
1 3 6 9 \begin{array}{llll}1 & 3 & 6&9\end{array} 1369
【样例输出】
117 \begin{array}{llll}117\end{array} 117
【评测用例规模与约定】
对于 30 % 30 \% 30% 的数据, 1 ≤ n ≤ 1000 , 1 ≤ a i ≤ 100 1 \leq n \leq 1000,1 \leq a_{i} \leq 100 1≤n≤1000,1≤ai≤100 。
对于所有评测用例, 1 ≤ n ≤ 200000 , 1 ≤ a i ≤ 1000 1 \leq n \leq 200000,1 \leq a_{i} \leq 1000 1≤n≤200000,1≤ai≤1000 。
试题 D: GCD
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 10 分
【问题描述】
给定两个不同的正整数 a , b a, b a,b, 求一个正整数 k k k 使得 gcd ( a + k , b + k ) \operatorname{gcd}(a+k, b+k) gcd(a+k,b+k) 尽可能大, 其中 gcd ( a , b ) \operatorname{gcd}(a, b) gcd(a,b) 表示 a a a 和 b b b 的最大公约数, 如果存在多个 k k k, 请输出所有满足条件的 k k k 中最小的那个。
【输入格式】
输入一行包含两个正整数 a , b a, b a,b, 用一个空格分隔。
【输出格式】
输出一行包含一个正整数 k k k 。
【样例输入】
5 7 \begin{array}{llll}5& 7\end{array} 57
【样例输出】
1 \begin{array}{llll}1 \end{array} 1
【评测用例规模与约定】
对于 20 % 20 \% 20% 的评测用例, a < b ≤ 1 0 5 a<b \leq 10^{5} a<b≤105;
对于 40 % 40 \% 40% 的评测用例, a < b ≤ 1 0 9 a<b \leq 10^{9} a<b≤109 ;
对于所有评测用例, 1 ≤ a < b ≤ 1 0 18 1 \leq a<b \leq 10^{18} 1≤a<b≤1018 。
试题 E: 蜂巢
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 15 分
【问题描述】
蜂巢由大量的六边形拼接而成, 定义蜂巢中的方向为: 0 表示正西方向, 1 表示西偏北 6 0 ∘ , 2 60^{\circ}, 2 60∘,2 表示东偏北 6 0 ∘ , 3 60^{\circ}, 3 60∘,3 表示正东, 4 表示东偏南 6 0 ∘ , 5 60^{\circ}, 5 60∘,5 表示西偏南 6 0 ∘ 60^{\circ} 60∘ 。
对于给定的一点 O O O, 我们以 O O O 为原点定义坐标系, 如果一个点 A A A 由 O O O 点先向 d d d 方向走 p p p 步再向 ( d + 2 ) m o d 6 (d+2) \bmod 6 (d+2)mod6 方向 ( d d d 的顺时针 12 0 ∘ 120^{\circ} 120∘ 方向) 走 q q q 步到达, 则这个点的坐标定义为 ( d , p , q ) (d, p, q) (d,p,q) 。在蜂窝中, 一个点的坐标可能有多种。
下图给出了点 B ( 0 , 5 , 3 ) B(0,5,3) B(0,5,3) 和点 C ( 2 , 3 , 2 ) C(2,3,2) C(2,3,2) 的示意。
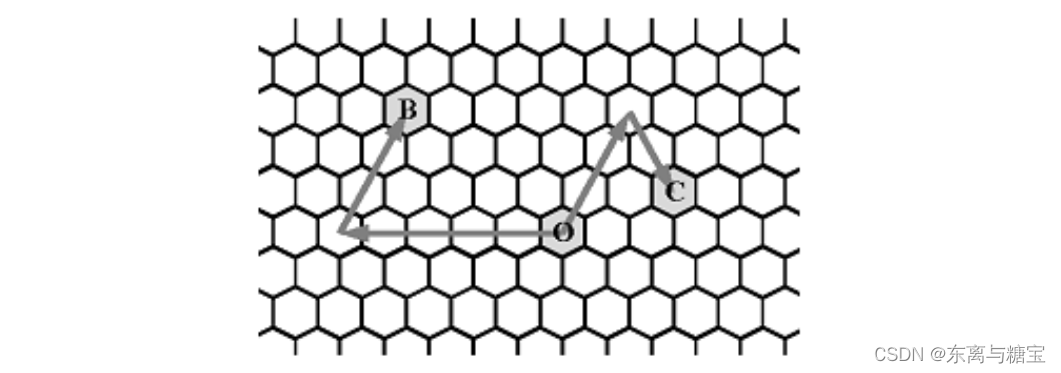
给定点 ( d 1 , p 1 , q 1 ) \left(d_{1}, p_{1}, q_{1}\right) (d1,p1,q1) 和点 ( d 2 , p 2 , q 2 ) \left(d_{2}, p_{2}, q_{2}\right) (d2,p2,q2), 请问他们之间最少走多少步可以到达?
【输入格式】
输入一行包含 6 个整数 d 1 , p 1 , q 1 , d 2 , p 2 , q 2 d_{1}, p_{1}, q_{1}, d_{2}, p_{2}, q_{2} d1,p1,q1,d2,p2,q2 表示两个点的坐标, 相邻两个整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示两点之间最少走多少步可以到达。
【样例输入】
0 5 3 2 3 2 \begin{array}{llllll}0 & 5 & 3 & 2 & 3 & 2\end{array} 053232
【样例输出】
7 \begin{array}{llllll}7\end{array} 7
【评测用例规模与约定】
对于 25 % 25 \% 25% 的评测用例, p 1 , p 2 ≤ 1 0 3 p_{1}, p_{2} \leq 10^{3} p1,p2≤103;
对于 50 % 50 \% 50% 的评测用例, p 1 , p 2 ≤ 1 0 5 p_{1}, p_{2} \leq 10^{5} p1,p2≤105;
对于 75 % 75 \% 75% 的评测用例, p 1 , p 2 ≤ 1 0 7 p_{1}, p_{2} \leq 10^{7} p1,p2≤107;
对于所有评测用例, 0 ≤ d 1 , d 2 ≤ 5 , 0 ≤ q 1 < p 1 ≤ 1 0 9 , 0 ≤ q 2 < p 2 ≤ 1 0 9 0 \leq d_{1}, d_{2} \leq 5,0 \leq q_{1}<p_{1} \leq 10^{9}, 0 \leq q_{2}<p_{2} \leq 10^{9} 0≤d1,d2≤5,0≤q1<p1≤109,0≤q2<p2≤109 。
试题 F : \mathrm{F}: F: 全排列的价值
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 15 分
【问题描述】
对于一个排列 A = ( a 1 , a 2 , ⋯ , a n ) A=\left(a_1, a_2, \cdots, a_n\right) A=(a1,a2,⋯,an), 定义价值 c i c_i ci 为 a 1 a_1 a1 至 a i − 1 a_{i-1} ai−1 中小于 a i a_i ai 的数的个数, 即 c i = ∣ { a j ∣ j < i , a j < a i } ∣ c_i=\left|\left\{a_j \mid j<i, a_j<a_i\right\}\right| ci=∣{aj∣j<i,aj<ai}∣ 。定义 A A A 的价值为 ∑ i = 1 n c i \sum_{i=1}^n c_i ∑i=1nci 。
给定 n n n, 求 1 至 n n n 的全排列中所有排列的价值之和。
【输入格式】
输入一行包含一个整数 n n n 。
【输出格式】
输出一行包含一个整数表示答案, 由于所有排列的价值之和可能很大, 请输出这个数除以 998244353 的余数。
【样例输入 1】
3 \begin{array}{llllll} 3 \end{array} 3
【样例输出 1】
9 \begin{array}{llllll}9\end{array} 9
【样例输入 2】
2022 \begin{array}{llllll}2022\end{array} 2022
【样例输出 2】
593300958 \begin{array}{llllll}593300958\end{array} 593300958
【样例说明】
1 至 3 构成的所有排列的价值如下:
( 1 , 2 , 3 ) : 0 + 1 + 2 = 3 (1,2,3): 0+1+2=3 (1,2,3):0+1+2=3;
( 1 , 3 , 2 ) : 0 + 1 + 1 = 2 (1,3,2): 0+1+1=2 (1,3,2):0+1+1=2;
( 2 , 1 , 3 ) : 0 + 0 + 2 = 2 (2,1,3): 0+0+2=2 (2,1,3):0+0+2=2;
( 2 , 3 , 1 ) : 0 + 1 + 0 = 1 (2,3,1): 0+1+0=1 (2,3,1):0+1+0=1;
( 3 , 1 , 2 ) : 0 + 0 + 1 = 1 (3,1,2): 0+0+1=1 (3,1,2):0+0+1=1;
( 3 , 2 , 1 ) : 0 + 0 + 0 = 0 (3,2,1): 0+0+0=0 (3,2,1):0+0+0=0;
故总和为 3 + 2 + 2 + 1 + 1 = 9 3+2+2+1+1=9 3+2+2+1+1=9 。
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例, n ≤ 20 n \leq 20 n≤20 ;
对于 70 % 70 \% 70% 的评测用例, n ≤ 5000 n \leq 5000 n≤5000 ;
对于所有评测用例, 2 ≤ n ≤ 1 0 6 2 \leq n \leq 10^{6} 2≤n≤106 。
试题 G: 青蛙过河
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 20 分
【问题描述】
小青蛙住在一条河边, 它想到河对岸的学校去学习。小青蛙打算经过河里的石头跳到对岸。
河里的石头排成了一条直线, 小青蛙每次跳跃必须落在一块石头或者岸上。不过, 每块石头有一个高度, 每次小肖蛙从一块石头起跳, 这块石头的高度就会下降 1, 当石头的高度下降到 0 时小青蛙不能再跳到这块石头上(某次跳跃后使石头高度下降到 0 是允许的)。
小青蛙一共需要去学校上 x x x 天课, 所以它需要往返 2 x 2 x 2x 次。当小青蛙具有一个跳跃能力 y y y 时, 它能跳不超过 y y y 的距离。
请问小青蛙的跳跃能力至少是多少才能用这些石头上完 x x x 次课。
【输入格式】
输入的第一行包含两个整数 n , x n, x n,x, 分别表示河的宽度和小青蛙需要去学校的天数。请注意 2 x 2 x 2x 才是实际过河的次数。
第二行包含 n − 1 n-1 n−1 个非负整数 H 1 , H 2 , ⋯ , H n − 1 H_{1}, H_{2}, \cdots, H_{n-1} H1,H2,⋯,Hn−1, 其中 H i > 0 H_{i}>0 Hi>0 表示在河中与小青蛙的家相距 i i i 的地方有一块高度为 H i H_{i} Hi 的石头, H i = 0 H_{i}=0 Hi=0 表示这个位置没有石头。
【输出格式】
输出一行, 包含一个整数, 表示小青蛙需要的最低跳跃能力。
【样例输入】
5 1 \begin{array}{llll}5 &1 \end{array} 51
1 0 1 0 \begin{array}{llll}1 & 0 & 1 & 0\end{array} 1010
【样例输出】
4 \begin{array}{llll}4\end{array} 4
【样例解释】
由于只有两块高度为 1 的石头, 所以往返只能各用一块。第 1 块石头和对岸的距离为 4 , 如果小青蛙的跳跃能力为 3 则无法满足要求。所以小青蛙最少需要 4 的跳跃能力。
【评测用例规模与约定】
对于 30 % 30 \% 30% 的评测用例, n ≤ 100 n \leq 100 n≤100 ;
对于 60 % 60 \% 60% 的评测用例, n ≤ 1000 n \leq 1000 n≤1000;
对于所有评测用例, 1 ≤ n ≤ 1 0 5 , 1 ≤ x ≤ 1 0 9 , 1 ≤ H i ≤ 1 0 4 1 \leq n \leq 10^{5}, 1 \leq x \leq 10^{9}, 1 \leq H_{i} \leq 10^{4} 1≤n≤105,1≤x≤109,1≤Hi≤104 。
试题 H \mathrm{H} H : 因数平方和
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0MB 本题总分: 20 分
【问题描述】
记 f ( x ) f(x) f(x) 为 x x x 的所有因数的平方的和。例如: f ( 12 ) = 1 2 + 2 2 + 3 2 + 4 2 + 6 2 + f(12)=1^{2}+2^{2}+3^{2}+4^{2}+6^{2}+ f(12)=12+22+32+42+62+ 1 2 2 12^{2} 122 。
定义 g ( n ) = ∑ i = 1 n f ( i ) g(n)=\sum_{i=1}^{n} f(i) g(n)=∑i=1nf(i) 。给定 n n n, 求 g ( n ) g(n) g(n) 除以 1 0 9 + 7 10^{9}+7 109+7 的余数。
【输入格式】
输入一行包含一个正整数 n n n 。
【输出格式】
输出一个整数表示答案 g ( n ) g(n) g(n) 除以 1 0 9 + 7 10^{9}+7 109+7 的余数。
【样例输入】
100000 \begin{array}{llll}100000 \end{array} 100000
【样例输出】
680584257 \begin{array}{llll}680584257 \end{array} 680584257
【评测用例规模与约定】
对于 20 % 20 \% 20% 的评测用例, n ≤ 1 0 5 n \leq 10^{5} n≤105 。
对于 30 % 30 \% 30% 的评测用例, n ≤ 1 0 7 n \leq 10^{7} n≤107 。
对于所有评测用例, 1 ≤ n ≤ 1 0 9 1 \leq n \leq 10^{9} 1≤n≤109 。
试题 I: 最优清零方案
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 25 分
【问题描述】
给定一个长度为 N N N 的数列 A 1 , A 2 , ⋯ , A N A_{1}, A_{2}, \cdots, A_{N} A1,A2,⋯,AN 。现在小蓝想通过若干次操作将这个数列中每个数字清零。
每次操作小蓝可以选择以下两种之一:
选择一个大于 0 的整数, 将它减去 1 ;选择连续 K K K 个大于 0 的整数, 将它们各减去 1 。小蓝最少经过几次操作可以将整个数列清零?
【输入格式】
输入第一行包含两个整数 N N N 和 K K K 。
第二行包含 N N N 个整数 A 1 , A 2 , ⋯ , A N A_{1}, A_{2}, \cdots, A_{N} A1,A2,⋯,AN 。
【输出格式】
输出一个整数表示答案。
【样例输入】
4 2 \begin{array}{llll}4&2\end{array} 42
1 2 3 4 \begin{array}{llll}1 & 2 & 3 & 4\end{array} 1234
【样例输出】
6 \begin{array}{llll}6\end{array} 6
【评测用例规模与约定】
对于 20 % 20 \% 20% 的评测用例, 1 ≤ K ≤ N ≤ 10 1 \leq K \leq N \leq 10 1≤K≤N≤10 。
对于 40 % 40 \% 40% 的评测用例, 1 ≤ K ≤ N ≤ 100 1 \leq K \leq N \leq 100 1≤K≤N≤100 。
对于 50 % 50 \% 50% 的评测用例, 1 ≤ K ≤ N ≤ 1000 1 \leq K \leq N \leq 1000 1≤K≤N≤1000 。
对于 60 % 60 \% 60% 的评测用例, 1 ≤ K ≤ N ≤ 10000 1 \leq K \leq N \leq 10000 1≤K≤N≤10000 。
对于 70 % 70 \% 70% 的评测用例, 1 ≤ K ≤ N ≤ 100000 1 \leq K \leq N \leq 100000 1≤K≤N≤100000 。
对于所有评测用例, 1 ≤ K ≤ N ≤ 1000000 , 0 ≤ A i ≤ 1000000 1 \leq K \leq N \leq 1000000,0 \leq A_{i} \leq 1000000 1≤K≤N≤1000000,0≤Ai≤1000000 。
试题 J : \mathrm{J}: J: 推导部分和
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 25 分
【问题描述】
对于一个长度为 N N N 的整数数列 A 1 , A 2 , ⋯ A N A_{1}, A_{2}, \cdots A_{N} A1,A2,⋯AN, 小蓝想知道下标 l l l 到 r r r 的部分和 ∑ i = l r = A l + A l + 1 + ⋯ + A r \sum_{i=l}^{r}=A_{l}+A_{l+1}+\cdots+A_{r} ∑i=lr=Al+Al+1+⋯+Ar 是多少?
然而, 小蓝并不知道数列中每个数的值是多少, 他只知道它的 M M M 个部分和的值。其中第 i i i 个部分和是下标 l i l_{i} li 到 r i r_{i} ri 的部分和 ∑ j = l i r i = A l i + A l i + 1 + ⋯ + A r i \sum_{j=l_{i}}^{r_{i}}=A_{l_{i}}+A_{l_{i}+1}+\cdots+A_{r_{i}} ∑j=liri=Ali+Ali+1+⋯+Ari,值是 S i S_{i} Si 。
【输入格式】
第一行包含 3 个整数 N 、 M N 、 M N、M 和 Q Q Q 。分别代表数组长度、已知的部分和数量和询问的部分和数量。
接下来 M M M 行, 每行包含 3 个整数 l i , r i , S i l_{i}, r_{i}, S_{i} li,ri,Si 。
接下来 Q Q Q 行, 每行包含 2 个整数 l l l 和 r r r, 代表一个小蓝想知道的部分和。
【输出格式】
对于每个询问, 输出一行包含一个整数表示答案。如果答案无法确定, 输出 UNKNOWN。
【样例输入】
5 3 3 \begin{array}{llll}5&3&3 \end{array} 533
1 5 15 \begin{array}{llll}1&5&15 \end{array} 1515
4 5 9 \begin{array}{llll}4&5&9 \end{array} 459
2 3 5 \begin{array}{llll}2&3&5 \end{array} 235
1 5 \begin{array}{llll}1&5 \end{array} 15
1 3 \begin{array}{llll}1&3 \end{array} 13
1 2 \begin{array}{llll}1&2 \end{array} 12
【样例输出】
15 \begin{array}{llll}15\end{array} 15
6 \begin{array}{llll}6 \end{array} 6
【评测用例规模与约定】
对于 10 % 10 \% 10% 的评测用例, 1 ≤ N , M , Q ≤ 10 , − 100 ≤ S i ≤ 100 1 \leq N, M, Q \leq 10,-100 \leq S_{i} \leq 100 1≤N,M,Q≤10,−100≤Si≤100 。
对于 20 % 20 \% 20% 的评测用例, 1 ≤ N , M , Q ≤ 20 , − 1000 ≤ S i ≤ 1000 1 \leq N, M, Q \leq 20,-1000 \leq S_{i} \leq 1000 1≤N,M,Q≤20,−1000≤Si≤1000 。
对于 30 % 30 \% 30% 的评测用例, 1 ≤ N , M , Q ≤ 50 , − 10000 ≤ S i ≤ 10000 1 \leq N, M, Q \leq 50,-10000 \leq S_{i} \leq 10000 1≤N,M,Q≤50,−10000≤Si≤10000 。
对于 40 % 40 \% 40% 的评测用例, 1 ≤ N , M , Q ≤ 1000 , − 1 0 6 ≤ S i ≤ 1 0 6 1 \leq N, M, Q \leq 1000,-10^{6} \leq S_{i} \leq 10^{6} 1≤N,M,Q≤1000,−106≤Si≤106 。
对于 60 % 60 \% 60% 的评测用例, 1 ≤ N , M , Q ≤ 10000 , − 1 0 9 ≤ S i ≤ 1 0 9 1 \leq N, M, Q \leq 10000,-10^{9} \leq S_{i} \leq 10^{9} 1≤N,M,Q≤10000,−109≤Si≤109 。
对于所有评测用例, 1 ≤ N , M , Q ≤ 1 0 5 , − 1 0 12 ≤ S i ≤ 1 0 12 , 1 ≤ l i ≤ r i ≤ N 1 \leq N, M, Q \leq 10^{5},-10^{12} \leq S_{i} \leq 10^{12}, 1 \leq l_{i} \leq r_{i} \leq N 1≤N,M,Q≤105,−1012≤Si≤1012,1≤li≤ri≤N, 1 ≤ l ≤ r ≤ N 1 \leq l \leq r \leq N 1≤l≤r≤N 。数据保证没有矛盾。







