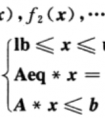您现在的位置是：首页 > 唯美句子

基于遗传算法的多目标优化算法(matlab实现)

作者：胡椒时间：2024-03-22 14:42:56分类：唯美句子

简介　　文章浏览阅读6.1k次，点赞7次，收藏106次。接着进行的是前端中的拥挤距离计算。①根据设定的系数ParetoFraction计算第一前端中允许保留的个体数目，按照一定的公式计算其余前端中允许保留的个体数目，则某前端中保留的个体数目为min{允许保留的个体数目

点击全文阅读

1 理论基础

1.1 多目标优化及Pareto最优解

        多目标优化问题可以描述如下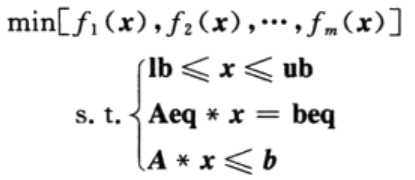：         其中，f(x)为待优化的目标函数；x为待优化的变量；Ib和ub分别为变量x的下限和上限约束；Aeq*x=beq为变量x的线性等式约束；A*x≤b为变量x的线性不等式约束。         在图1所示的优化问题中，目标函数f1 和f2是相互矛盾的。因为A1<B1且A2>B2,也就是说，某一个目标函数的提高需要以另一个目标函数的降低作为代价，称这样的解A和解B是非劣解(noninferiority solutions),或者说是Pareto最优解(Pareto optima)。多目标优化算法的目的就是要寻找这些Pareto最优解。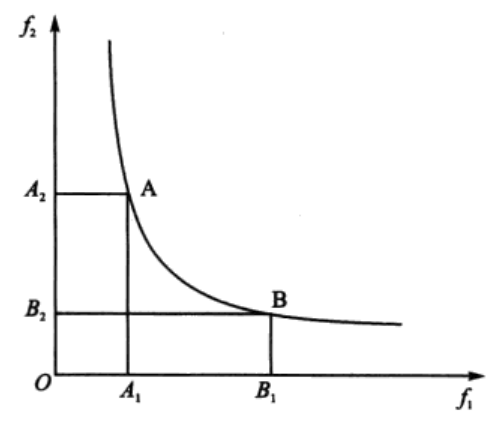

 图1 多目标优化问题

1.2 函数gamultiobj

        目前的多目标优化算法有很多，Kalyanmoy Deb的带精英策略的快速非支配排序遗传算法(nondominated sorting genetic algorithm I,NSGA-II)无疑是其中应用最为广泛也是最为成功的一种。MATLAB R2009a版本提供的函数gamultiobj所采用的算法就是基于NSGA-Ⅱ改进的一种多目标优化算法(a variant of NSGA-ⅡI)。函数gamultiobj的出现，为在MATLAB平台下解决多目标优化问题提供了良好的途径。函数gamultiobj包含在遗传算法与直接搜索工具箱(genetic algorithm and direct search toolbox,GADST)中，其位置如下：MATLAB安装目录\toolbox\gads\gads,这里称函数gamultiobj为基于遗传算法的多目标优化函数，相应的算法为基于遗传算法的多目标优化算法。本案例将以函数gamultiobj为基础，对基于遗传算法的多目标优化算法进行详细分析，并介绍函数gamultiobj的使用。

1.3 函数gamultiobj中的一些基本概念

        在讲解函数gamultiobj之前，有必要介绍基于遗传算法的多目标优化算法中的一些概念，其他的概念如个体、种群、代、选择、交叉、变异和交叉后代比例等，这里不做介绍。事实上，由于函数gamultiobj是基于遗传算法的，因此，遗传算法中的很多概念和这里的函数gamultiobj是相同的，这也是函数gamultiobj位于GADST内的原因。         1.支配(dominate)与非劣(non-inferior)在多目标优化问题中，如果个体p至少有一个目标比个体q的好，而且个体p的所有目标都不比个体q的差，那么称个体p支配个体q(p dominates q),或者称个体q受个体p支配(gis dominated by p),也可以说，个体p非劣于个体q(p is non-inferior to q)。         2.序值(rank)和前端(front)         如果p支配q,那么p的序值比q的低。如果p和q互不支配，或者说，p和q相互非劣，那么p和q有相同的序值。序值为1的个体属于第一前端，序值为2的个体属于第二前端，依次类推。显然，在当前种群中，第一前端是完全不受支配的，第二前端受第一前端中个体的支配。这样，通过排序，可以将种群中的个体分到不同的前端。         3.拥挤距离(crowding distance)         拥挤距离用来计算某前端中的某个体与该前端中其他个体之间的距离，用以表征个体间的拥挤程度。显然，拥挤距离的值越大，个体间就越不拥挤，种群的多样性就越好。需要指出的是，只有处于同一前端的个体间才需要计算拥挤距离，不同前端之间的个体计算拥挤距离是没有意义的         4.最优前端个体系数(ParetoFraction)         最优前端个体系数定义为最优前端中的个体在种群中所占的比例，即最优前端个体数=min{ParetoFraction×种群大小，前端中现存的个体数目},其取值范围为0～1,详细讲解见3.2节中的函数trimPopulation。需要指出的是，ParetoFraction的概念是函数gamultiobj所特有的，在NSGA-Ⅱ中是没有的，这也是为什么称函数gamultiobj是一种多目标优化算法的原因。

2 素例背景

2.1 问题描述

        待优化的多目标问题表述如下：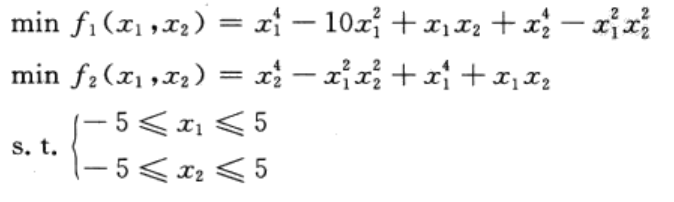

2.2 解题思路及步骤

        这里将使用函数gamultiobj求解以上多目标优化问题。同函数ga的调用一样，函数gamultiobj的调用方式也有两种：GUI方式和命令行方式。 1:通过GUI方式调用函数gamultiobj         通过以下两种方式可以调出函数gamultiobj的GUI界面：         (1)在MATLAB主界面的左下角依次单击：APP→Optimization→在Slover中选择“gamultiobj—Multiobjective optimization using Genetic Algorithm"。

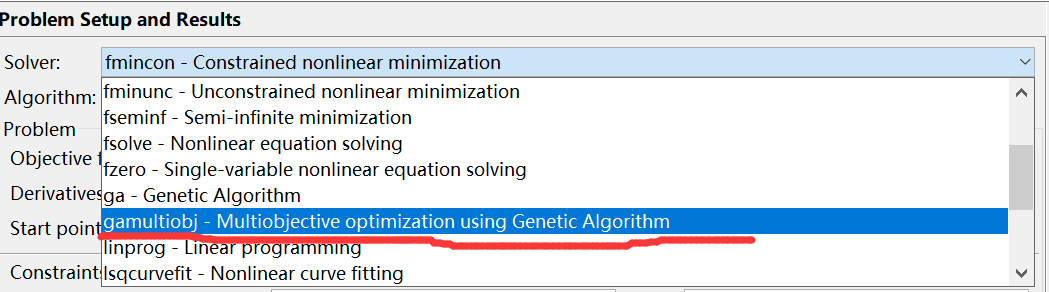
        (2)在命令行调用GUI： 

optimtool('gamultiobj')
        可以看到，函数gamultiobj的GUI界面与函数ga的GUI界面大致相同，仅在以下几个方面存在区别，         (1)前者比后者多了Distance measure function和Pareto front population fraction两个 参数。         (2)前者比后者少了参数Elite count,这是因为函数gamultiobj的精英是自动保留的;前者比后者少了Scaling function,这是因为函数gamultiobj的选择是基于序值和拥挤距离的，故不再需要Scaling的处理；函数gamultiobj没有非线性约束。         (3)绘图函数不同及下列设置的默认值不同：种群大小(Population size)、选择函数 (Selection function)、交叉函数(Crossover function)、最大进化代数(Generations)、停止代数 (Stall generations)、适应度函数值偏差(Function tolerance)。         函数gamultiobj GUI界面的其他介绍和使用方法可以参考普通遗传算法，这里不再介绍。 2:通过调用函数的形式使用gamultiobj         以下内容引用自官方文档：

gamultiobj是使用遗传算法解决多目标优化问题的函数。它试图解决以下形式的多目标问题：
min F（X） subject to: AX <= b, AeqX = beq (线性约束)
X lb <= X <= ub (边界约束)

X = gamultiobj（FITNESSFCN，NVARS）找到在FITNESSFCN中定义的目标函数的局部帕累托集X。NVARS是优化问题的维数（决策变量的数量）。FITNESSFCN接受大小为1-by-NVARS的向量X，并返回在决策变量处评估的大小为1-by-numberOfObjectives的向量。X是具有NVARS列的矩阵。X中的行数与帕累托解的数量相同。帕累托集中的所有解同样优，取决于应用程序的设计者选择帕累托集中的解。

X = gamultiobj（FITNESSFCN，NVARS，A，b）找到在FITNESSFCN中定义的目标函数的局部帕累托集X，受制于线性不等式A*X <= B。仅支持默认的PopulationType选项（'doubleVector'）的线性约束；不支持其他种群类型，例如'bitString'和'custom'。

X = gamultiobj（FITNESSFCN，NVARS，A，b，Aeq，beq）找到在FITNESSFCN中定义的目标函数的局部帕累托集X，受制于线性等式AeqX = beq以及线性不等式AX <= b。（如果不存在不等式，则设置A=[]和b=[]。）仅支持默认的PopulationType选项（'doubleVector'）的线性约束；不支持其他种群类型，例如'bitString'和'custom'。

X = gamultiobj（FITNESSFCN，NVARS，A，b，Aeq，beq，lb，ub）定义设计变量X的下限和上限，以便在范围lb <= X <= ub中找到局部帕累托集。如果不存在边界，则使用空矩阵。如果X（i）无下限，则设置lb（i）= -Inf；如果X（i）无上限，则设置ub（i）= Inf。仅支持默认的PopulationType选项（'doubleVector'）的边界约束；不支持其他种群类型，例如'bitString'和'custom'。

X = gamultiobj（FITNESSFCN，NVARS，A，b，Aeq，beq，lb，ub，NONLCON）找到满足NONLCON中定义的约束的局部帕累托集X。函数NONLCON接受X并返回向量C和Ceq，分别表示非线性不等式和等式。帕累托集X必须满足C（X）<=0和Ceq（X）=0。如果不存在边界，则设置lb=[]和/或ub=[]。当PopulationType选项设置为'bitString'或'custom'时，不满足非线性约束。有关详细信息，请参见文档。

X = gamultiobj（FITNESSFCN，NVARS，A，b，Aeq，beq，lb，ub，NONLCON，options）使用OPTIONS中的值替换默认优化参数，找到帕累托集X。OPTIONS可以通过OPTIMOPTIONS函数创建。有关详细信息，请参见OPTIMOPTIONS。有关gamultiobj接受的选项列表，请参见文档。

X = gamultiobj（PROBLEM）查找PROBLEM的最小值。PROBLEM是具有以下字段的结构：
fitnessfcn：<Fitness function>
nvars：<Number of design variables>
Aineq：<不等式约束的A矩阵>
bineq：<不等式约束的b向量>
Aeq：<等式约束的Aeq矩阵>
beq：<等式约束的beq向量>
lb：<X的下限>
ub：<X的上限>
nonlcon：<非线性约束函数>
options：<使用optimoptions（'gamultiobj'，...）创建的选项>
solver：<solver name 'gamultiobj'>
rngstate：<随机数生成器的状态>

[X，FVAL] = gamultiobj（FITNESSFCN，NVARS，...）还返回矩阵FVAL，FITNESSFCN中定义的所有目标函数在X的所有解中的值。FVAL具有numberOfObjectives列，行数与X相同。

[X，FVAL，EXITFLAG] = gamultiobj（FITNESSFCN，NVARS，...）还返回描述gamultiobj的退出条件的EXITFLAG。EXITFLAG的可能值以及相应的退出条件为

1：在options.MaxStallGenerations代内帕累托集的扩展的平均值的值的变化小于options.FunctionTolerance。
0：超过最大代数。
-1：由输出或绘图函数终止优化。
-2：未找到可行点。
-5：超时。

[X，FVAL，EXITFLAG，OUTPUT] = gamultiobj（FITNESSFCN，NVARS，...）还返回带有以下字段的结构OUTPUT：
rngstate：<GA开始前随机数生成器的状态>
generations：<总代数，不包括HybridFcn迭代>
funccount：<函数评估的总数>
maxconstraint：<最大约束违规（如果有）>
message：<gamultiobj终止消息>

[X，FVAL，EXITFLAG，OUTPUT，POPULATION] = gamultiobj（FITNESSFCN，...）在终止时还返回最终POPULATION。

[X，FVAL，EXITFLAG，OUTPUT，POPULATION，SCORE] = gamultiobj（FITNESSFCN，...）在终止时还返回最终POPULATION的SCORE。

3 MATLAB程序实现

3.1 gamultiobj组织结构

        MATLAB自带的基于遗传算法的多目标优化函数gamultiobj的组织结构如图2所示。可以看到，在函数gamultiobj中，先调用函数gacommon确定优化问题的约束类型，然后调用函数gamultiobjsolve对多目标优化问题进行求解。在函数gamultiobjsolve中，先调用函数gamultiobjMakeState产生初始种群，接着判断是否可以退出算法，若退出，则得到Pareto最优解，若不退出，则调用函数stepgamultiobj使种群进化一代，然后调用函数gadsplot进行绘图，并调用函数gmultiobjConverged判断终止条件。可以看到，在以上循环迭代过程中，函数tepgamultiobj是关键函数，下面将对该函数进行讲解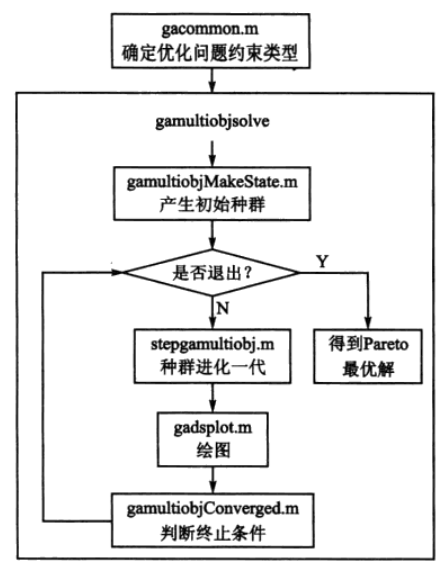

3.2 函数stepgamultiobj分析

1.函数stepgamultiobj结构及图形描述         函数stepgamultiobj的代码位于：MATLAB安装目录\toolbox\gads\gads\private,其结构如图3所示。

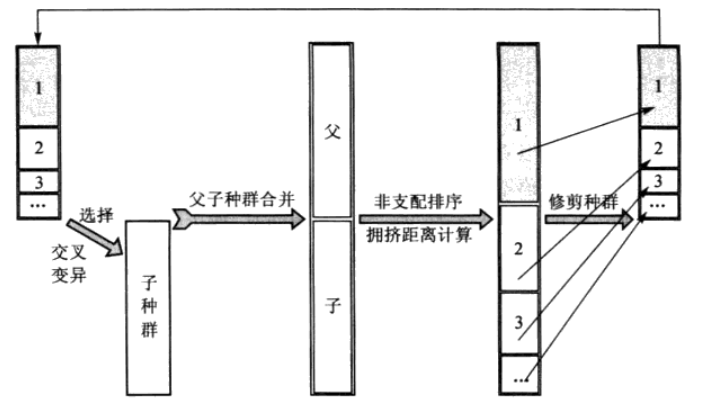        图4形象地表达了函数stepgamultiobj的过程，其中的大框表示种群，种群被分为若干前端，标有数字的小框表示前端，相应的数字表示该前端的序值，相应的操作及所用的函数与图3一致。         2.选择(selectiontournament.m)         不同于函数ga,函数gamultiobj的选择操作只使用锦标赛选择(selectiontournament),程序代码如下： 

function parents = selectiontournament(expectation,nParents,options,tournamentSize)if nargin < 4 || isempty(tournamentSize)    tournamentSize = 4;end% Choose the playersplayerlist = ceil(size(expectation,1) * rand(nParents,tournamentSize));% Play tournamentparents = tournament(playerlist,expectation);function champions = tournament(playerlist,expectation)%tournament between players based on their expectationplayerSize = size(playerlist,1);champions = zeros(1,playerSize);% For each set of playersfor i = 1:playerSize    players = playerlist(i,:);    % For each tournament    winner = players(1); % Assume that the first player is the winner    for j = 2:length(players) % Winner plays against each other consecutively        score1 = expectation(winner,:);        score2 = expectation(players(j),:);        if score2(1) > score1(1)             winner = players(j);        elseif score2(1) == score1(1)            try % socre(2) may not be present for single objective problems                if score2(2) > score1(2)                    winner = players(j);                end            catch            end        end    end    champions(i) = winner;end
        从以上代码的分析中可以看出，函数gamultiobj的选择操作是基于序值和拥挤距离的，具体地说，对于两个个体，当序值不同时，序值小的个体将被选中而不论其拥挤距离如何，这是因为“如果p支配q,那么p的序值比q的低”;当序值相同时，拥挤距离大的个体将被选中，这是因为拥挤距离越大，种群多样性越好。序值和拥挤距离的赋值在函数stepgamultiobj中通过[-rank,Distance]巧妙地实现。 3.交叉、变异、产生子种群和父子种群合并         函数gamultiobj默认的交叉函数和变异函数分别为函数crossoverintermediate和函数 mutationadaptfeasible,实现的功能与函数ga是一致的，这里不再展开。需要说明的是，由于函数gamultiobj中使用了支配和排序的思想，其精英是自动保留的，因此，不再具有函数ga中的精英保留操作，父子种群的合并通过函数stepgamultiobj中的以下语句实现： 
population=[population;nextPopulation];
4.计算序值和拥挤距离         函数rankAndDistance依次调用函数nonDominatedRank、函数DistanceMeasureFcn和函数trimPopulation,下面分别介绍。 (1)函数nonDominatedRank         非支配排序函数nonDominatedRank的作用是对父、子种群合并后的种群中的个体进行排序。非支配排序函数nonDominatedRank的基本思想是：序值rankCounter从1开始，依次加1,在每一轮rankCounter中，依次将种群中未被排序(判断个体是否已被排序的矩阵每轮更新一次)的个体p与其余所有未被排序的个体q进行比较，检查个体q是否支配个体p,若否，则个体p被赋予当前序值rankCounter;反之，因为个体p受个体q支配，故个体p的序值高于当前rankCounter,应参与下一轮的排序。通过排序，种群中的所有个体被分到了不同的前端。接着进行的是前端中的拥挤距离计算。 (2)函数DistanceMeasureFcn         拥挤距离计算函数DistanceMeasureFcn的作用是计算某一前端内每个个体与其相邻个体的距离，与函数nonDominatedRank计算出的序值一起，为函数selectiontournament的选择提供依据，同时，也为接下来的函数trimPopulation做好准备。默认的拥挤距离计算函数是distancecrowding,         拥挤距离计算函数DistanceMeasureFcn的基本思想是：对多目标中的每一个目标，分别计算一次相应的拥挤距离，再将这些拥挤距离相加得到最后的拥挤距离。在每个目标对应的拥挤距离的计算中，前端两头的两个个体的拥挤距离为inf,其余个体的拥挤距离为与该个体相邻的前后两个个体在(一1,1)区间映射后的目标函数值之差，这里的相邻是指同一前端中个体间的目标函数值大小接近。显然，某个体的拥挤距离越大，表示该个体与相邻个体的目标函数值差别越大，也就是多样性越好，故在序值相同的条件下，在函数selectiontournament中就越应该被选中，在接下来的函数rimPopulation中就越不会被裁减掉。 (3)函数trimPopulation         由于父子种群的合并，使得函数rankAndDistance中的popSize为两倍的种群大小(该种群大小在options中设置，稍后述及),而函数rankAndDistance中的nParents即为种群大小，故其中的条件“nParents==popSize”不成立，需要调用函数trimPopulation以修剪种群。种群修剪函数trimPopulation的作用是：在两倍于种群大小的个体中修剪出个数等于种群大小的个体 种群修剪函数trimPopulation的基本思想是：         ①根据设定的系数ParetoFraction计算第一前端中允许保留的个体数目，按照一定的公式计算其余前端中允许保留的个体数目，则某前端中保留的个体数目为min{允许保留的个体数目，现存的个体数目},也就是说，对于第一前端，所设定的系数ParetoFraction直接决定了该前端中允许保留的个体数目，当允许保留的个体数目小于前端中现存的个体数目时，系数ParetoFraction所决定的允许保留的个体数目对该前端中保留的个体数目有限制作用，对于其他前端，也有类似思想。         ②某前端中保留的个体数目计算出来以后，剩下的就是执行了，也就是说，将该前端中的个体数目修剪至保留的个体数目，这是通过锦标赛选择实现的。前已述及，对于同一前端，个体的拥挤距离越小，则多样性越差，因此，在锦标赛选择中，就越应该成为失败者而被选中淘汰，这种思想与函数selectiontournament中将expectation赋值为[-rank,Distance]是异曲同工的。另外，个体的去除通过将其赋值为空矩阵巧妙地实现。         ③通过以上操作后，若保留下来的各前端的个体之和比Options中设置的种群大小多，那么需要进一步修剪，将最终的种群大小精减为Options中设置的种群大小。其中所用的思想与函数selectiontournament的选择思想也是一致的。         5.函数distanceAndSpread         该函数的作用是计算种群的平均距离和spread,后者参与图2中函数gamultiobjConverged对终止条件的判断。

3.3使用函数gamultiobj求解多目标优化问题

        (1)使用函数gamultiobj求解多目标优化问题的第一步是编写目标函数的M文件。对于以上问题，函数名为my_first_multi,目标函数代码如下： 
function f = my_first_multi(x) f(1) = x(1)^4 - 10*x(1)^2+x(1)*x(2) + x(2)^4 - (x(1)^2)*(x(2)^2);f(2) = x(2)^4 - (x(1)^2)*(x(2)^2) + x(1)^4 + x(1)*x(2);
        (2)使用命令行方式调用gamultiobj函数，代码如下： 
clearclc fitnessfcn = @my_first_multi;   % Function handle to the fitness functionnvars = 2;                      % Number of decision variableslb = [-5,-5];                   % Lower boundub = [5,5];                     % Upper boundA = []; b = [];                 % No linear inequality constraintsAeq = []; beq = [];             % No linear equality constraintsoptions = gaoptimset('ParetoFraction',0.3,'PopulationSize',100,'Generations',200,'StallGenLimit',200,'TolFun',1e-100,'PlotFcns',@gaplotpareto);[x,fval] = gamultiobj(fitnessfcn,nvars, A,b,Aeq,beq,lb,ub,options);
       其中，fitnessfcn即(1)中定义的目标函数M文件，设置的最优前端个体系数ParetoFraction为0.3,种群大小PopulationSize为100,最大进化代数Generations为200,停止代数StallGenLimit也为200,适应度函数值偏差TolFun为le-100,绘制Pareto前端。当然，也可以通过GUI方式调用函数gamultiobj,其方法与函数ga的调用相同，这里不再赘述。

3.4 结果分析

        可以看到，在基于遗传算法的多目标优化算法的运行过程中，自动绘制了第一前端中个体的分布情况，且分布随着算法进化一代而更新一次。当迭代停止后，得到如图5所示的第一前端个体分布图。同时，Worksapce中返回了函数gamultiobj得到的Pareto解集x及与x对应的目标函数值，如表1所列。需要说明的是，由于算法的初始种群是随机产生的，因此每次运行的结果不一样。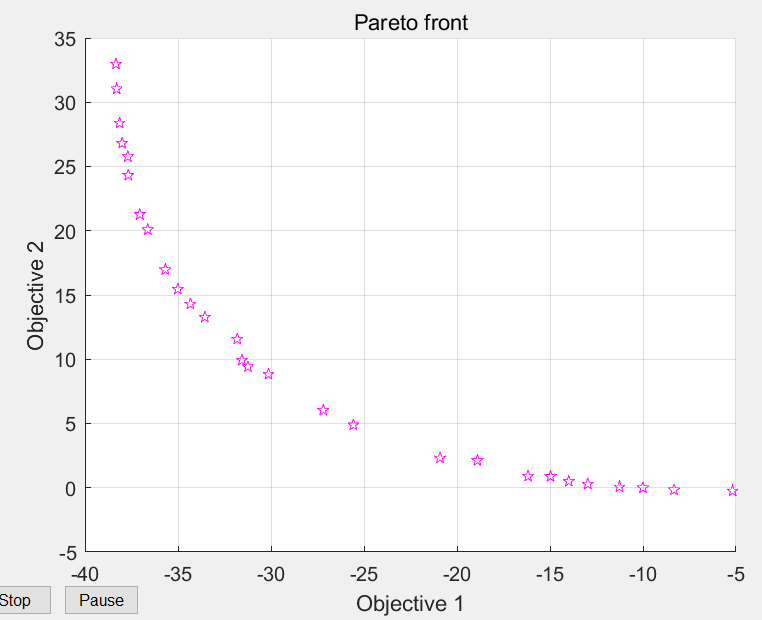

X1

X2

F1

F2

-0.702604978119867

0.702952585998864

-5.18650007950382

-0.249962526715632

-0.702604978119867

0.702952585998864

-5.18650007950382

-0.249962526715632

-2.67029628249862

1.97094984179847

-38.3329919666111

32.9718303966485

-2.63333082043443

1.96439479904977

-38.2990862211675

31.0452258773312

-2.08276662583749

1.31511944032696

-31.8120240265547

11.5671441504702

-1.15140918299647

0.929595004170188

-12.9690674486452

0.288363618240700

-2.24644109783116

1.74843483243066

-35.0074620102752

15.4575140499734

-2.41514714936595

1.79906399485147

-37.0545025942865

21.2748549366181

-2.38150536923245

1.86154289865626

-36.6275981206039

20.0880801162262

-1.82290570989828

1.23859537968056

-27.1897975855276

6.04005468627002

-1.30683826246950

1.00106276130680

-16.1770194512696

0.901242991273376

-2.51924521816231

1.97762256309168

-37.6944252011462

25.7715394911906

-1.52418626573825

1.14877588640926

-20.9096383290698

2.32179939758130

-1.06426303292729

0.940627721164028

-11.2640394037852

0.0625186287707547

-2.03691502287105

1.46637748311609

-31.5605834251883

9.92964467878934

-1.25902473471341

0.812532300017947

-14.9724017318298

0.879031094371823

-2.54579676153300

1.91445377012727

-38.0010331247212

26.8097783855977

-1.20396912943971

1.11637502706332

-13.9916338566617

0.503782789776543

-2.48983479640961

1.85584414778789

-37.6715458295670

24.3212273045537

-2.20516184528621

1.75854178206263

-34.3335326972675

14.2938549417933

-2.01646480190617

1.57180853250172

-31.2393168080679

9.42198616519718

-2.29454764988585

1.76104970025566

-35.6807426169950

16.9687465589719

-1.45000820746889

1.40337975638453

-18.9015806104910

2.12365740678036

-1.97425293081786

1.31617729318077

-30.1344339638333

8.84231238459566

-1.74540792332427

1.19107078666463

-25.5718188853058

4.89266930272549

-2.67029628249862

1.97094984179847

-38.3329919666111

32.9718303966485

-0.903690328921961

0.874168873899340

-8.32972021598921

-0.163158110118390

-1.00010614649929

0.757833629162209

-10.0042121434185

-0.00208910076199753

-2.16416470915156

1.47815692188379

-33.5583157841867

13.2777730991840

-2.57929181596638

1.94522918966795

-38.1411557075827

28.3863070115286

        从图5可以看到，第一前端的Pareto最优解分布均匀。从表1可以看到，返回的Pareto最优解个数为30个，而种群大小为100,可见，ParetoFraction为0.3的设置发挥了作用。另外，个体被限制在了[-5,5]的上下限范围内。

点击全文阅读

郑重声明：

本站所有活动均为互联网所得，如有侵权请联系本站删除处理

上一篇：Web 前端—HTML+CSS系列

下一篇：返回列表

随便看看

我来说两句

本栏最新

本栏热门

全站热门

Copyright 2018 Inc. AllRights Reserved. Design by 一句子网 豫ICP备2022018965号-7

一句子 www.hlwxy.com