目录
1、三角函数2、双曲函数3、指数和对数函数4、幂函数5、误差和伽玛函数6、舍入和余数函数7、浮点操作函数8、最小值、最大值、差值函数9、其他函数10、宏11、比较宏头文件声明了一组用于计算常见数学运算和转换的函数:
1、三角函数
cos(x):计算余弦。返回x弧度角的余弦值。#include <stdio.h> #include <math.h> #define PI 3.14159265int main (){ double param, result; param = 60.0; result = cos ( param * PI / 180.0 ); printf ("The cosine of %f degrees is %f.\n", param, result ); return 0;}sin(x):计算正弦。返回x弧度角的正弦值。The cosine of 60.000000 degrees is 0.500000.
#include <stdio.h> #include <math.h> #define PI 3.14159265int main(){double param, result;param = 30.0;result = sin(param * PI / 180);printf("The sine of %f degrees is %f.\n", param, result);return 0;}tan(x):计算正切。返回x弧度角的正切值。The sine of 30.000000 degrees is 0.500000.
#include <stdio.h> #include <cmath> #define PI 3.14159265int main(){double param, result;param = 45.0;result = tan(param * PI / 180.0);printf("The tangent of %f degrees is %f.\n", param, result);return 0;}acos(x):计算反余弦。返回x的反余弦的主值,用弧度表示。The tangent of 45.000000 degrees is 1.000000.
#include <iostream> #include <cmath> #define PI 3.14159265int main(){double param, result;param = 0.5;result = acos(param) * 180.0 / PI;printf("The arc cosine of %f is %f degrees.\n", param, result);return 0;}asin(x):计算反正弦。返回x的反正弦的主值,用弧度表示。The arc cosine of 0.500000 is 60.000000 degrees.
#include <iostream> #include <cmath> #define PI 3.14159265int main(){double param, result;param = 0.5;result = asin(param) * 180.0 / PI;printf("The arc sine of %f is %f degrees\n", param, result);return 0;}atan(x):计算反正切。返回x的反正切的主值,用弧度表示。请注意,由于符号模糊,该函数无法仅通过正切值确定角度落在哪个象限。请参见atan2(),了解采用分数参数的替代方法。The arc sine of 0.500000 is 30.000000 degrees
#include <iostream> #include <cmath> #define PI 3.14159265int main(){double param, result;param = 1.0;result = atan(param) * 180 / PI;printf("The arc tangent of %f is %f degrees\n", param, result);return 0;}atan2(y,x):计算反正切。返回y/x反正切的主值,用弧度表示。如果传递的两个参数都为零,则会发生域错误。The arc tangent of 1.000000 is 45.000000 degrees
#include <iostream> #include <cmath> #define PI 3.14159265int main(){double x, y, result;x = -10.0;y = 10.0;result = atan2(y, x) * 180 / PI;printf("The arc tangent for (x=%f, y=%f) is %f degrees\n", x, y, result);return 0;}The arc tangent for (x=-10.000000, y=10.000000) is 135.000000 degrees
2、双曲函数
cosh(x):计算双曲余弦。返回x的双曲余弦值,x是表示双曲线角度的值。#include <iostream> #include <cmath> int main(){double param, result;param = log(2.0);result = cosh(param);printf("The hyperbolic cosine of %f is %f.\n", param, result);return 0;}sinh(x):计算双曲正弦。返回x的双曲正弦值,x是表示双曲线角度的值。The hyperbolic cosine of 0.693147 is 1.250000.
#include <iostream> #include <cmath> int main(){double param, result;param = log(2.0);result = sinh(param);printf("The hyperbolic sine of %f is %f.\n", param, result);return 0;}tanh(x):计算双曲正切。返回x双曲正切值。The hyperbolic sine of 0.693147 is 0.750000.
#include <iostream> #include <cmath> int main(){double param, result;param = log(2.0);result = tanh(param);printf("The hyperbolic tangent of %f is %f.\n", param, result);return 0;}acosh(x):计算双曲反余弦。返回x的非负面积双曲反余弦值。如果参数x小于1,则会发生域错误。The hyperbolic tangent of 0.693147 is 0.600000.
#include <iostream> #include <cmath> int main(){double param, result;param = exp(2) - sinh(2);result = acosh(param);printf("The area hyperbolic cosine of %f is %f radians.\n", param, result);return 0;}asinh(x):计算双曲反正弦。返回x的双曲正弦面积。The area hyperbolic cosine of 3.762196 is 2.000000 radians.
#include <iostream> #include <cmath> int main(){double param, result;param = exp(2) - cosh(2);result = asinh(param);printf("The area hyperbolic sine of %f is %f.\n", param, result);return 0;}atanh(x):计算双曲反正切。返回x的双曲正切面积。面积双曲正切是双曲正切的逆运算。计算其双曲正切面积的值,在区间[-1,+1]内。 如果参数超出此区间,则会发生域错误。 对于-1和+1的值,可能会出现极点误差。The area hyperbolic sine of 3.626860 is 2.000000.
#include <iostream> #include <cmath> int main(){double param, result;param = tanh(1);result = atanh(param);printf("The area hyperbolic tangent of %f is %f.\n", param, result);return 0;}The area hyperbolic tangent of 0.761594 is 1.000000.
3、指数和对数函数
exp(x):计算指数函数。返回x的以e为底的指数函数,它是e的x次方: e x e^x ex。#include <iostream> #include <cmath> int main (){ double param, result; param = 5.0; result = exp (param); printf ("The exponential value of %f is %f.\n", param, result ); return 0;}frexp():得到有效位数和指数。将浮点数x分解为它的二进制有效位(绝对值在0.5(包括)和1.0(不包括)之间的浮点)和2的整数指数: x = s i g n i f i c a n d ∗ 2 e x p o n e n t x = significand * 2 ^{exponent} x=significand∗2exponent。The exponential value of 5.000000 is 148.413159.
exponent存储在exp指向的位置,significand是函数返回的值。如果x为零,则两部分(有效数和指数)都为零。
如果x为负,则该函数返回的有效数字为负。
#include <iostream> #include <cmath> int main (){ double param, result; int n; param = 8.0; result = frexp (param , &n); printf ("%f = %f * 2^%d\n", param, result, n); return 0;}ldexp():从有效数和指数生成值。返回x(有效数)乘以2的指数幂(指数)的结果。 l e x p r ( x , e x p ) = x ∗ 2 e x p lexpr(x,exp) = x * 2^ {exp} lexpr(x,exp)=x∗2exp8.000000 = 0.500000 * 2^4
#include <iostream> #include <cmath> int main (){ double param, result; int n; param = 0.95; n = 4; result = ldexp (param , n); printf ("%f * 2^%d = %f\n", param, n, result); return 0;}log(x):计算自然对数。返回x的自然对数。如果参数x为负,则会发生域错误;如果x为零,可能会导致极点错误(取决于库实现)。0.950000 * 2^4 = 15.200000
#include <iostream> #include <cmath> int main (){ double param, result; param = 5.5; result = log (param); printf ("log(%f) = %f\n", param, result ); return 0;}log10(x):计算公对数。返回以10为底x的自然对数。如果参数为负,则会发生域错误。log(5.500000) = 1.704748
#include <iostream> #include <cmath> int main (){ double param, result; param = 1000.0; result = log10 (param); printf ("log10(%f) = %f\n", param, result ); return 0;}modf (x , * intpart):分解成整数和小数部分。将x分解成整数和小数部分。 整数部分存储在intpart指向的对象中,小数部分由函数返回。 这两部分的符号与x相同。log10(1000.000000) = 3.000000
#include <iostream> #include <cmath> int main (){ double param, fractpart, intpart; param = 3.14159265; fractpart = modf (param , &intpart); printf ("%f = %f + %f \n", param, intpart, fractpart); return 0;}exp2 (x):以2为底的指数函数。返回x的以2为底的指数函数,它是2的x次方: 2 x 2^x 2x。3.141593 = 3.000000 + 0.141593
#include <iostream> #include <cmath> int main (){ double param, result; param = 8.0; result = exp2 (param); printf ("2 ^ %f = %f.\n", param, result ); return 0;}expm1(x):计算指数- 1。返回e的x次幂减1: e x − 1 e^x-1 ex−1。对于x的小幅度值,expm1可能比exp(x)-1更精确。2 ^ 8.000000 is 256.000000.
#include <iostream> #include <cmath> int main(){double param, result;param = 1.0;result = expm1(param);printf("expm1 (%f) = %f.\n", param, result);return 0;}ilogb(x):整数对数。使用FLT_RADIX 作为对数的底数,返回|x|的对数的整数部分。expm1 (1.000000) = 1.718282.
#include <iostream> #include <cmath> int main (){ double param; int result; param = 10.0; result = ilogb (param); printf ("ilogb(%f) = %d\n", param, result); return 0;}log1p(x):返回1加x的自然对数。对于x的小幅度值,logp1可能比log(1+x)更精确.如果参数x小于-1,则会发生域错误。ilogb(10.000000) = 3
#include <iostream> #include <cmath> int main (){ double param, result; param = 1.0; result = log1p (param); printf ("log1p (%f) = %f.\n", param, result ); return 0;}log2(x):返回x以2为底的对数。 如果参数x为负,则会发生域错误。log1p (1.000000) = 0.693147
#include <iostream> #include <cmath> int main (){ double param, result; param = 1024.0; result = log2 (param); printf ("log2 (%f) = %f.\n", param, result ); return 0;}logb(x):返回以FLT基数为底数的|x|的对数。 在大多数平台上,FLT基数是2,因此这个函数对于正值相当于log2。log2 (1024.000000) = 10.000000
#include <iostream> #include <cmath> int main (){ double param, result; param = 1024.0; result = logb (param); printf ("logb (%f) = %f.\n", param, result ); return 0;}scalbn(x,n):标度x乘以FLT基数的n次幂,返回的值: s c a l b n ( x , n ) = x ∗ F L T 基数 n scalbn(x,n) = x * {FLT基数}^n scalbn(x,n)=x∗FLT基数n,x和n是系统中一个浮点数的组成部分;在这种情况下,该函数可以被优化为比显式计算该值的理论运算更有效。 在大多数平台上,FLT基数是2,这使得这个函数相当于ldexp。logb (1024.000000) = 10.000000
#include <iostream> #include <cmath> int main (){ double param, result; int n; param = 1.50; n = 4; result = scalbn (param , n); printf ("%f * %d^%d = %f\n", param, FLT_RADIX, n, result); return 0;}scalbln(x,n):与上一个函数用法相同,只是这里的n是1.500000 * 2^4 = 24.000000
long int类型 #include <iostream> #include <cmath> int main (){ double param, result; long n; param = 1.50; n = 4L; result = scalbln (param , n); printf ("%f * %d^%d = %f\n", param, FLT_RADIX, n, result); return 0;}1.500000 * 2^4 = 24.000000
4、幂函数
pow():返回底数的幂指数。#include <iostream> #include <cmath> int main (){ printf ("7 ^ 3 = %f\n", pow (7.0, 3.0) ); printf ("4.73 ^ 12 = %f\n", pow (4.73, 12.0) ); printf ("32.01 ^ 1.54 = %f\n", pow (32.01, 1.54) ); return 0;}sqrt(x):返回x的平方根。 如果参数为负,则会发生域错误。7 ^ 3 = 343.000000
4.73 ^ 12 = 125410439.217423
32.01 ^ 1.54 = 208.036691
#include <iostream> #include <cmath> int main (){ double param, result; param = 1024.0; result = sqrt (param); printf ("sqrt(%f) = %f\n", param, result ); return 0;}cbrt(x):返回x的立方根。sqrt(1024.000000) = 32.000000
#include <iostream> #include <cmath> int main (){ double param, result; param = 27.0; result = cbrt (param); printf ("cbrt (%f) = %f\n", param, result); return 0;}hypot(x,y):该函数返回x和y的平方和的平方根(根据勾股定理),但不会导致中间值的过度上溢或下溢。cbrt (27.000000) = 3.000000
#include <iostream> #include <cmath> int main(){double leg_x, leg_y, result;leg_x = 3;leg_y = 4;result = hypot(leg_x, leg_y);printf("%f, %f and %f form a right-angled triangle.\n", leg_x, leg_y, result);return 0;}3.000000, 4.000000 and 5.000000 form a right-angled triangle.
5、误差和伽玛函数
erf(x):返回x的误差函数值。计算公式: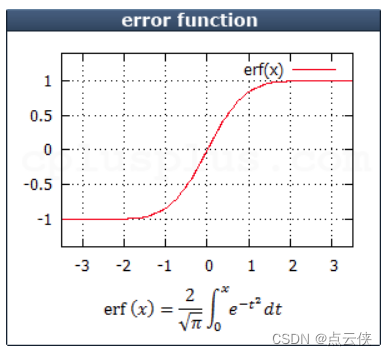
#include <iostream> #include <cmath> int main (){ double param, result; param = 1.0; result = erf (param); printf ("erf (%f) = %f\n", param, result ); return 0;}erfc (x):返回x的互补误差函数值。互补误差函数相当于:erfc(x) = 1-erf(x)。计算公式:erf (1.000000) = 0.842701

#include <iostream> #include <cmath> int main (){ double param, result; param = 1.0; result = erfc (param); printf ("erfc(%f) = %f\n", param, result ); return 0;}tgamma (x):返回x的伽玛函数。计算公式:erfc (1.000000) = 0.157299
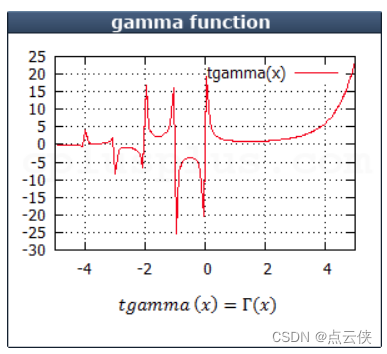
#include <iostream> #include <cmath> int main (){ double param, result; param = 0.5; result = tgamma (param); printf ("tgamma(%f) = %f\n", param, result ); return 0;}lgamma(x):返回x的伽玛函数绝对值的自然对数。计算公式:tgamma (0.500000) = 1.772454

#include <iostream> #include <cmath> int main (){ double param, result; param = 0.5; result = lgamma (param); printf ("lgamma(%f) = %f\n", param, result ); return 0;}lgamma (0.500000) = 0.572365
6、舍入和余数函数
ceil(x):向上取整,返回不小于x的最小整数值。#include <iostream> #include <cmath> int main (){ printf ( "ceil of 2.3 is %.1f\n", ceil(2.3) ); printf ( "ceil of 3.8 is %.1f\n", ceil(3.8) ); printf ( "ceil of -2.3 is %.1f\n", ceil(-2.3) ); printf ( "ceil of -3.8 is %.1f\n", ceil(-3.8) ); return 0;}floor(x):向下取整,返回不大于x的最大整数值。ceil of 2.3 is 3.0
ceil of 3.8 is 4.0
ceil of -2.3 is -2.0
ceil of -3.8 is -3.0
#include <iostream> #include <cmath> int main (){ printf ( "floor of 2.3 is %.1lf\n", floor (2.3) ); printf ( "floor of 3.8 is %.1lf\n", floor (3.8) ); printf ( "floor of -2.3 is %.1lf\n", floor (-2.3) ); printf ( "floor of -3.8 is %.1lf\n", floor (-3.8) ); return 0;}fmod(x):计算除法的余数。返回numer/denom的浮点余数(向零舍入):fmod = numer - tquot * denom。其中tquot是numer/denom的截断(即向零舍入)结果。类似的函数remainder返回相同的结果,但商被舍入到最接近的整数(而不是被截断)。floor of 2.3 is 2.0
floor of 3.8 is 3.0
floor of -2.3 is -3.0
floor of -3.8 is -4.0
#include <iostream> #include <cmath> int main (){ printf ( "fmod of 5.3 / 2 is %f\n", fmod (5.3,2) ); printf ( "fmod of 18.5 / 4.2 is %f\n", fmod (18.5,4.2) ); return 0;}trunc(x):将x向零舍入,返回幅度不大于x的最近整数值。fmod of 5.3 / 2 is 1.300000
fmod of 18.5 / 4.2 is 1.700000
#include <iostream> #include <cmath> int main (){ const char * format = "%.1f \t%.1f \t%.1f \t%.1f \t%.1f\n"; printf ("value\tround\tfloor\tceil\ttrunc\n"); printf ("-----\t-----\t-----\t----\t-----\n"); printf (format, 2.3,round( 2.3),floor( 2.3),ceil( 2.3),trunc( 2.3)); printf (format, 3.8,round( 3.8),floor( 3.8),ceil( 3.8),trunc( 3.8)); printf (format, 5.5,round( 5.5),floor( 5.5),ceil( 5.5),trunc( 5.5)); printf (format,-2.3,round(-2.3),floor(-2.3),ceil(-2.3),trunc(-2.3)); printf (format,-3.8,round(-3.8),floor(-3.8),ceil(-3.8),trunc(-3.8)); printf (format,-5.5,round(-5.5),floor(-5.5),ceil(-5.5),trunc(-5.5)); return 0;}
#include <iostream> #include <cmath> int main (){ const char * format = "%.1f \t%.1f \t%.1f \t%.1f \t%.1f\n"; printf ("value\tround\tfloor\tceil\ttrunc\n"); printf ("-----\t-----\t-----\t----\t-----\n"); printf (format, 2.3,round( 2.3),floor( 2.3),ceil( 2.3),trunc( 2.3)); printf (format, 3.8,round( 3.8),floor( 3.8),ceil( 3.8),trunc( 3.8)); printf (format, 5.5,round( 5.5),floor( 5.5),ceil( 5.5),trunc( 5.5)); printf (format,-2.3,round(-2.3),floor(-2.3),ceil(-2.3),trunc(-2.3)); printf (format,-3.8,round(-3.8),floor(-3.8),ceil(-3.8),trunc(-3.8)); printf (format,-5.5,round(-5.5),floor(-5.5),ceil(-5.5),trunc(-5.5)); return 0;}
long int类型的值返回。 #include <iostream> #include <cmath> int main (){ printf ( "lround (2.3) = %ld\n", lround(2.3) ); printf ( "lround (3.8) = %ld\n", lround(3.8) ); printf ( "lround (-2.3) = %ld\n", lround(-2.3) ); printf ( "lround (-3.8) = %ld\n", lround(-3.8) ); return 0;}llround(x):返回最接近x的整数值,中间情况从零开始四舍五入。舍入值作为Rounding using to-nearest rounding:
lround (2.3) = 2
lround (3.8) = 4
lround (-2.3) = -2
lround (-3.8) = -4
long long int类型的值返回。 #include <iostream> #include <cmath> int main (){ printf ( "llround (2.3) = %lld\n", llround(2.3) ); printf ( "llround (3.8) = %lld\n", llround(3.8) ); printf ( "llround (-2.3) = %lld\n", llround(-2.3) ); printf ( "llround (-3.8) = %lld\n", llround(-3.8) ); return 0;}rint(x):使用fegetround指定的舍入方向将x舍入为整数值。Rounding using to-nearest rounding:
llround (2.3) = 2
llround (3.8) = 4
llround (-2.3) = -2
llround (-3.8) = -4
/* rint example */#include <stdio.h> /* printf */#include <fenv.h> /* fegetround, FE_* */#include <math.h> /* rint */int main (){ printf ("rounding using "); switch (fegetround()) { case FE_DOWNWARD: printf ("downward"); break; case FE_TONEAREST: printf ("to-nearest"); break; case FE_TOWARDZERO: printf ("toward-zero"); break; case FE_UPWARD: printf ("upward"); break; default: printf ("unknown"); } printf (" rounding:\n"); printf ( "rint (2.3) = %.1f\n", rint(2.3) ); printf ( "rint (3.8) = %.1f\n", rint(3.8) ); printf ( "rint (-2.3) = %.1f\n", rint(-2.3) ); printf ( "rint (-3.8) = %.1f\n", rint(-3.8) ); return 0;}lrint(x):使用fegetround指定的舍入方向将x舍入为整数值,并将其作为Rounding using to-nearest rounding:
rint (2.3) = 2.0
rint (3.8) = 4.0
rint (-2.3) = -2.0
rint (-3.8) = -4.0
long int类型的值返回。 /* lrint example */#include <stdio.h> /* printf */#include <fenv.h> /* fegetround, FE_* */#include <math.h> /* lrint */int main (){ printf ("rounding using "); switch (fegetround()) { case FE_DOWNWARD: printf ("downward"); break; case FE_TONEAREST: printf ("to-nearest"); break; case FE_TOWARDZERO: printf ("toward-zero"); break; case FE_UPWARD: printf ("upward"); break; default: printf ("unknown"); } printf (" rounding:\n"); printf ( "lrint (2.3) = %ld\n", lrint(2.3) ); printf ( "lrint (3.8) = %ld\n", lrint(3.8) ); printf ( "lrint (-2.3) = %ld\n", lrint(-2.3) ); printf ( "lrint (-3.8) = %ld\n", lrint(-3.8) ); return 0;}llrint(x):使用fegetround指定的舍入方向将x舍入为整数值,并将其作为Rounding using to-nearest rounding:
lrint (2.3) = 2
lrint (3.8) = 4
lrint (-2.3) = -2
lrint (-3.8) = -4
long long int类型的值返回。 /* llrint example */#include <stdio.h> /* printf */#include <fenv.h> /* fegetround, FE_* */#include <math.h> /* llrint */int main (){ printf ("rounding using "); switch (fegetround()) { case FE_DOWNWARD: printf ("downward"); break; case FE_TONEAREST: printf ("to-nearest"); break; case FE_TOWARDZERO: printf ("toward-zero"); break; case FE_UPWARD: printf ("upward"); break; default: printf ("unknown"); } printf (" rounding:\n"); printf ( "llrint (2.3) = %lld\n", llrint(2.3) ); printf ( "llrint (3.8) = %lld\n", llrint(3.8) ); printf ( "llrint (-2.3) = %lld\n", llrint(-2.3) ); printf ( "llrint (-3.8) = %lld\n", llrint(-3.8) ); return 0;}nearbyint(x):使用fegetround指定的舍入方向将x舍入为整数值。Rounding using to-nearest rounding:
llrint (2.3) = 2
llrint (3.8) = 4
llrint (-2.3) = -2
llrint (-3.8) = -4
/* nearbyint example */#include <stdio.h> /* printf */#include <fenv.h> /* fegetround, FE_* */#include <math.h> /* nearbyint */int main (){ printf ("rounding using "); switch (fegetround()) { case FE_DOWNWARD: printf ("downward"); break; case FE_TONEAREST: printf ("to-nearest"); break; case FE_TOWARDZERO: printf ("toward-zero"); break; case FE_UPWARD: printf ("upward"); break; default: printf ("unknown"); } printf (" rounding:\n"); printf ( "nearbyint (2.3) = %.1f\n", nearbyint(2.3) ); printf ( "nearbyint (3.8) = %.1f\n", nearbyint(3.8) ); printf ( "nearbyint (-2.3) = %.1f\n", nearbyint(-2.3) ); printf ( "nearbyint (-3.8) = %.1f\n", nearbyint(-3.8) ); return 0;}remainder():返回numer/denom的浮点余数(四舍五入):remainder = numer - rquot * denom。其中rquot是numer/denom的结果,向最近的整数值舍入(中间情况向偶数舍入)。一个类似的函数fmod返回相同的结果,但是商被截断(四舍五入为零)。函数remquo的行为与此函数相同,但它还提供了对所用中间商值的访问。Rounding using to-nearest rounding:
nearbyint (2.3) = 2.0
nearbyint (3.8) = 4.0
nearbyint (-2.3) = -2.0
nearbyint (-3.8) = -4.0
#include <iostream> #include <cmath> int main(){printf("remainder of 5.3 / 2 is %f\n", remainder(5.3, 2));printf("remainder of 18.5 / 4.2 is %f\n", remainder(18.5, 4.2));return 0;}remquo():计算余数和商。返回的值与remainder相同,但它还存储了内部用于确定其结果的商。quot所指的值包含整数商num/denom的至少3位的同余模。remainder of 5.3 / 2 is -0.700000
remainder of 18.5 / 4.2 is 1.700000
#include <iostream> #include <cmath> int main (){ double numer = 10.3; double denom = 4.5; int quot; double result = remquo (numer,denom,"); printf ("numerator: %f\n", numer); printf ("denominator: %f\n", denom); printf ("remainder: %f\n", result); printf ("quotient: %d\n", quot); return 0;}numerator: 10.300000
denominator: 4.500000
remainder: 1.300000
quotient: 2
7、浮点操作函数
copysign(x,y):返回一个大小为x,符号与y相同的值。#include <iostream> #include <cmath> int main(){printf("copysign ( 10.0,-1.0) = %f\n", copysign(10.0, -1.0));printf("copysign (-10.0,-1.0) = %f\n", copysign(-10.0, -1.0));printf("copysign (-10.0, 1.0) = %f\n", copysign(-10.0, 1.0));return 0;}copysign ( 10.0,-1.0) = -10.0
copysign (-10.0,-1.0) = -10.0
copysign (-10.0, 1.0) = 10.0
nan():返回double类型的静态NaN(非数字)值。NaN值用于标识浮点元素的未定义或不可表示的值,如负数的平方根或0/0的结果。库实现可以使用该参数以特定于实现的方式区分不同的NaN值。类似地,nanf和nanl分别返回float和long double类型的NaN值。
nextafter(x,y):返回x之后y方向的下一个可表示值。
#include <iostream> #include <cmath> int main(){printf("first representable value greater than zero: %e\n", nextafter(0.0, 1.0));printf("first representable value less than zero: %e\n", nextafter(0.0, -1.0));return 0;}nexttoward(x,y):返回x之后y方向的下一个可表示值。 该函数的行为类似于nextafter,但可能具有更精确的y。first representable value greater than zero: 4.940656e-324
first representable value less than zero: -4.940656e-324
#include <iostream> #include <cmath> int main (){ printf ("first representable value greater than zero: %e\n", nexttoward(0.0,1.0L)); printf ("first representable value less than zero: %e\n", nexttoward(0.0,-1.0L)); return 0;}first representable value greater than zero: 4.940656e-324
first representable value less than zero: -4.940656e-324
8、最小值、最大值、差值函数
fdim(x,y):返回x和y之间的正差值。 如果x>y,函数返回x-y,否则返回零。#include <iostream> #include <cmath> int main (){ printf ("fdim (2.0, 1.0) = %f\n", fdim(2.0,1.0)); printf ("fdim (1.0, 2.0) = %f\n", fdim(1.0,2.0)); printf ("fdim (-2.0, -1.0) = %f\n", fdim(-2.0,-1.0)); printf ("fdim (-1.0, -2.0) = %f\n", fdim(-1.0,-2.0)); return 0;}fmax(x,y):返回x和y较大的那个数。如果其中一个值是NaN,则返回另一个值。fdim (2.0, 1.0) = 1.000000
fdim (1.0, 2.0) = 0.000000
fdim (-2.0,-1.0) = 0.000000
fdim (-1.0,-2.0) = 1.000000
#include <iostream> #include <cmath> int main (){ printf ("fmax (100.0, 1.0) = %f\n", fmax(100.0,1.0)); printf ("fmax (-100.0, 1.0) = %f\n", fmax(-100.0,1.0)); printf ("fmax (-100.0, -1.0) = %f\n", fmax(-100.0,-1.0)); return 0;}fmin(x,y):返回x和y较小的那个数。如果其中一个值是NaN,则返回另一个值。fmax (100.0, 1.0) = 100.000000
fmax (-100.0, 1.0) = 1.000000
fmax (-100.0,-1.0) = -1.000000
#include <iostream> #include <cmath> int main (){ printf ("fmin (100.0, 1.0) = %f\n", fmin(100.0,1.0)); printf ("fmin (-100.0, 1.0) = %f\n", fmin(-100.0,1.0)); printf ("fmin (-100.0, -1.0) = %f\n", fmin(-100.0,-1.0)); return 0;}fmin (100.0, 1.0) = 1.000000
fmin (-100.0, 1.0) = -100.000000
fmin (-100.0,-1.0) = -100.000000
9、其他函数
fabs(x):返回x的绝对值:|x|。#include <iostream> #include <cmath> int main (){ printf ("The absolute value of 3.1416 is %f\n", fabs (3.1416) ); printf ("The absolute value of -10.6 is %f\n", fabs (-10.6) ); return 0;}abs(x):返回x的绝对值:|x|。The absolute value of 3.1416 is 3.141600
The absolute value of -10.6 is 10.600000
#include <iostream> #include <cmath> int main (){ std::cout << "abs (3.1416) = " << std::abs (3.1416) << '\n'; std::cout << "abs (-10.6) = " << std::abs (-10.6) << '\n'; return 0;}fma(x,y,z):返回 x*y+z。该函数计算结果时不会损失任何中间结果的精度。可以在实现中定义以下宏常数,以表示该函数通常比执行 x ∗ y + z x*y+z x∗y+z中的算术运算提供了效率改进(例如当使用硬件乘加指令时):abs (3.1416) = 3.1416
abs (-10.6) = 10.6

#include <iostream> #include <cmath> int main (){ double x,y,z,result; x = 10.0, y = 20.0, z = 30.0;#ifdef FP_FAST_FMA result = fma(x,y,z);#else result = x*y+z;#endif printf ("10.0 * 20.0 + 30.0 = %f\n", result); return 0;}10.0 * 20.0 + 30.0 = 230.000000
10、宏
fpclassify(x):根据x的值,返回与分类宏常量之一匹配的int类型的值:
请注意,每个值只属于一个类别:零不是正常值。
#include <iostream> #include <cmath> int main(){double d = 1.0 / 0.0;switch (fpclassify(d)) {case FP_INFINITE: printf("infinite"); break;case FP_NAN: printf("NaN"); break;case FP_ZERO: printf("zero"); break;case FP_SUBNORMAL: printf("subnormal"); break;case FP_NORMAL: printf("normal"); break;}if (signbit(d)) printf(" negative\n");else printf(" positive or unsigned\n");return 0;}isfinite(x):返回x是否为有限值。infinite positive or unsigned
#include <iostream> #include <cmath> int main(){ printf ("isfinite(0.0) : %d\n",isfinite(0.0)); printf ("isfinite(1.0/0.0) : %d\n",isfinite(1.0/0.0)); printf ("isfinite(-1.0/0.0) : %d\n",isfinite(-1.0/0.0)); printf ("isfinite(sqrt(-1.0)): %d\n",isfinite(sqrt(-1.0))); return 0;}isinf(x):返回x是否为无穷大值(正无穷大或负无穷大)。isfinite(0.0) : 1
isfinite(1.0/0.0) : 0
isfinite(-1.0/0.0) : 0
isfinite(sqrt(-1.0)): 0
#include <iostream> #include <cmath> int main(){ printf ("isinf(0.0) : %d\n",isinf(0.0)); printf ("isinf(1.0/0.0) : %d\n",isinf(1.0/0.0)); printf ("isinf(-1.0/0.0) : %d\n",isinf(-1.0/0.0)); printf ("isinf(sqrt(-1.0)): %d\n",isinf(sqrt(-1.0))); return 0;}isnan(x):返回x是否为NaN (Not-A-Number)值。NaN值用于标识浮点元素的未定义或不可表示的值,例如负数的平方根或0/0的结果。isinf(0.0) : 0
isinf(1.0/0.0) : 1
isinf(-1.0/0.0) : 1
isinf(sqrt(-1.0): 0
#include <iostream> #include <cmath> int main(){printf("isnan(sqrt(-1.0)): %d\n", isnan(sqrt(-1.0)));return 0;}isnormal(x):返回x是否为正常值:即,它是否既不是 infinity、NaN、零也不是subnormal。isnan(sqrt(-1.0)): 1
#include <iostream> #include <cmath> int main(){printf("isnormal(1.0) : %d\n", isnormal(1.0));return 0;}signbit(x):返回x的符号是否为负。该函数也可以应用于无穷大、nan和零(如果零是无符号的,它被认为是正数)。isnormal(1.0) : 1
#include <iostream> #include <cmath> int main(){printf("signbit(0.0) : %d\n", signbit(0.0));printf("signbit(sqrt(-1.0)): %d\n", signbit(sqrt(-1.0)));return 0;}signbit(0.0) : 0
signbit(sqrt(-1.0)): 1
11、比较宏
isgreater(x,y):返回x是否大于y,如果一个或两个参数都是NaN,则函数返回false。#include <iostream> #include <cmath> int main(){double result;result = log(10.0);if (isgreater(result, 0.0))printf("log(10.0) is positive");elseprintf("log(10.0) is not positive");return 0;}isgreaterequal(x,y):返回x是否大于或等于y。log(10.0) is positive
#include <iostream> #include <cmath> int main (){ double result; result = log (10.0); if (isgreaterequal(result,0.0)) printf ("log(10.0) is not negative"); else printf ("log(10.0) is negative"); return 0;}isless(x,y):返回x是否小于y,如果一个或两个参数都是NaN,则函数返回false。log(10.0) is not negative
#include <iostream> #include <cmath> int main (){ double result; result = log (10.0); if (isless(result,0.0)) printf ("log(10.0) is negative"); else printf ("log(10.0) is not negative"); return 0;}islessequal(x,y):返回x是否小于或等于y。log(10.0) is not negative
#include <iostream> #include <cmath> int main (){ double result; result = log (10.0); if (islessequal(result,0.0)) printf ("log(10.0) is not positive"); else printf ("log(10.0) is positive"); return 0;}islessgreater(x,y):返回x是小于还是大于y。log(10.0) is positive
#include <iostream> #include <cmath> int main (){ double result; result = log (10.0); if (islessgreater(result,0.0)) printf ("log(10.0) is not zero"); else printf ("log(10.0) is zero"); return 0;}isunordered(x,y):返回x或y是否为无序值:如果一个或两个参数都是NaN,则参数是无序的,函数返回true。log(10.0) is not zero
#include <iostream> #include <cmath> int main (){ double result; result = sqrt (-1.0); if (isunordered(result,0.0)) printf ("sqrt(-1.0) and 0.0 cannot be ordered"); else printf ("sqrt(-1.0) and 0.0 can be ordered"); return 0;}sqrt(-1.0) and 0.0 cannot be ordered