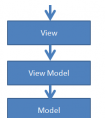
本文主要介绍如何在matlab中建立机械臂模型(前提要下载了Robotics Toolbox机器人工具箱~),并进行基于正逆运动学计算的轨迹运动。对于已有的Solidworks机械臂三维模型,如何导入Matlab,并对其进行运动控制。
关于机器人工具箱的安装及函数的详细解释可以参考这篇文章(写的很详细,很好!!):(1条消息) Matlab机器人工具箱(Robotics Toolbox)学习笔记_Mist_Orz的博客-CSDN博客
目录
1 机械臂的建立
核心函数——Link函数释义
机械臂仿真代码
2 基于运动学求解的轨迹规划
正逆运动学求解
3 基于Solidworks和Matlab 的自定义机械臂模型的导入及使用
将Solidworks模型导入Matlab
进行正运动学轨迹规划
1 机械臂的建立
核心函数——Link函数释义
Link函数是根据DH参数建立连杆,包含了关节的主要信息,建立连杆时DH参数的输入顺序为:关节转角θ,关节距离d,连杆长度a,连杆转角α,关节类型(0转动,1移动);
另外,关节变量的参数有:
qlim指定关节极限,【注意,工具箱中的移动关节变量不允许有负值】;
jointtype指定关节类型,默认为转动关节,L(4).jointtype='P’意味着第四根link是由移动关节连接的;
offset为关节初始值的偏置。【这里要注意的是,定义好关节类型后,相应的变量必须为0,初值必须由offset定义,例如,关节2为转动关节,那么L(2)的theta必须为0,但是我们又希望初始状态下关节2能有一个偏置,那么就在初始化后通过“ L(2).offset=pi/2;”的语句来实现】。
最后是建模参数类型的选择:标准型D-H参数 / 改进型D-H参数,区别在于固连坐标系不同以及执行变换的的顺序不同,类比如下:
| 标准型D-H参数 | 改进型D-H参数 | |
| 固连坐标系 的选用 | 以连杆的后一个关节坐标系为固连坐标系 | 以连杆的前一个关节坐标系为固连坐标系 |
| X轴方向 的确定 | 以当前Z轴和“前一个”坐标系的Z轴叉乘确定X轴 | 以“后一个”坐标的Z轴与当前Z轴叉乘确定X轴 |
| 坐标系间 的变换规则 | 相邻关节坐标系之间的参数变化顺序为: θ、d、a、α | 相邻关节坐标系之间的参数变化顺序为: α、a、θ、d |
Link函数调用的格式为
L(1) = Link([theta1, D1, A1, alpha1, offset1], 'standard') %标准型D-H参数L(1) = Link([theta1, D1, A1, alpha1, offset1], 'modified') %改进型D-H参数机械臂仿真代码
举例1:建立关节型六轴机械臂
%% 基于MATLAB的关节型六轴机械臂仿真%% 参数定义clear;close all;clc; %角度转换angle=pi/180; %转化为角度制 %D-H参数表theta1 = 0; D1 = 0.4; A1 = 0.025; alpha1 = pi/2; offset1 = 0;theta2 = pi/2;D2 = 0; A2 = 0.56; alpha2 = 0; offset2 = 0;theta3 = 0; D3 = 0; A3 = 0.035; alpha3 = pi/2; offset3 = 0;theta4 = 0; D4 = 0.515; A4 = 0; alpha4 = pi/2; offset4 = 0;theta5 = pi; D5 = 0; A5 = 0; alpha5 = pi/2; offset5 = 0;theta6 = 0; D6 = 0.08; A6 = 0; alpha6 = 0; offset6 = 0;%% DH法建立模型,关节转角,关节距离,连杆长度,连杆转角,关节类型(0转动,1移动),'standard':建立标准型D-H参数L(1) = Link([theta1, D1, A1, alpha1, offset1], 'standard')L(2) = Link([theta2, D2, A2, alpha2, offset2], 'standard')L(3) = Link([theta3, D3, A3, alpha3, offset3], 'standard')L(4) = Link([theta4, D4, A4, alpha4, offset4], 'standard')L(5) = Link([theta5, D5, A5, alpha5, offset5], 'standard')L(6) = Link([theta6, D6, A6, alpha6, offset6], 'standard')% 定义关节范围L(1).qlim =[-180*angle, 180*angle];L(2).qlim =[-180*angle, 180*angle];L(3).qlim =[-180*angle, 180*angle];L(4).qlim =[-180*angle, 180*angle];L(5).qlim =[-180*angle, 180*angle];L(6).qlim =[-180*angle, 180*angle];%% 显示机械臂(把上述连杆“串起来”)robot0 = SerialLink(L,'name','six');theta = [0 pi/2 0 0 pi 0];%初始关节角度figure(1)robot0.plot(theta);title('六轴机械臂模型');可得运行结果(第二张图分别标明六个轴):
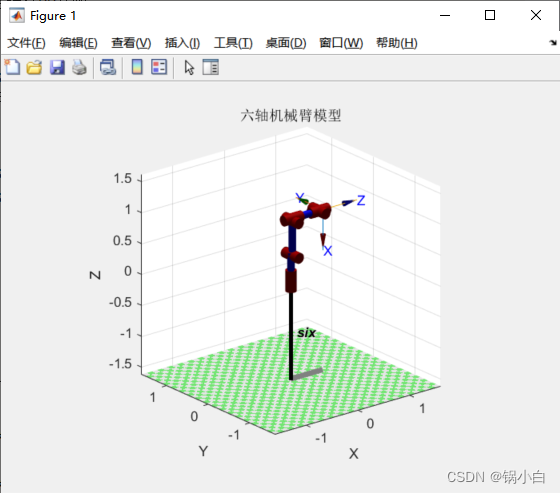
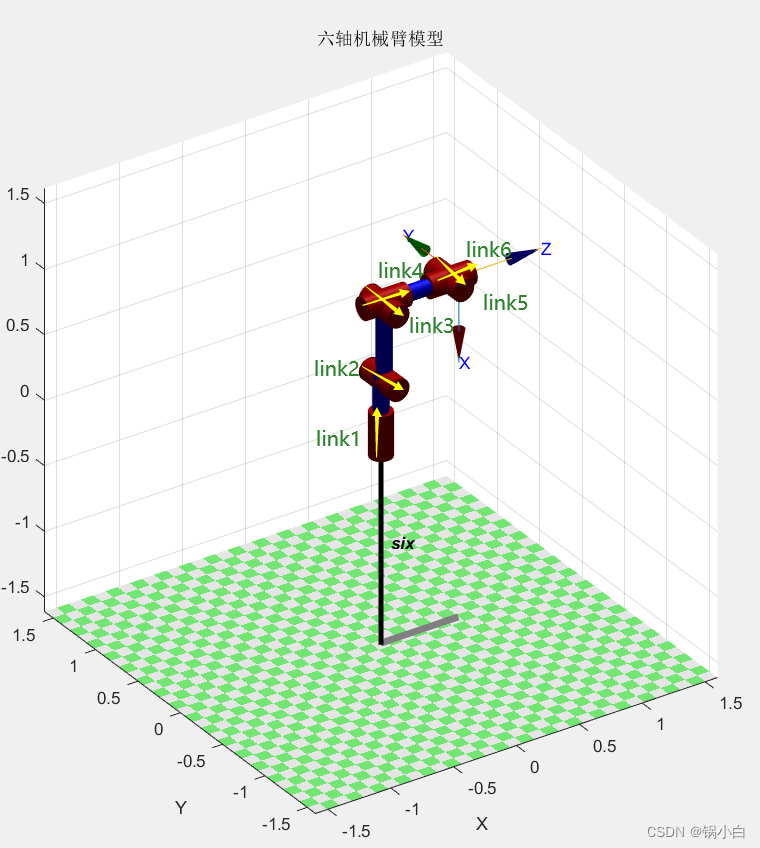
可示教:加入teach指令,使得机械臂关节角度可调节:
接续上一段代码继续执行:
%% 加入teach指令,则可调整各个关节角度robot1 = SerialLink(L,'name','sixsix');figure(2)robot1.plot(theta);robot1.teachtitle('六轴机械臂模型可调节');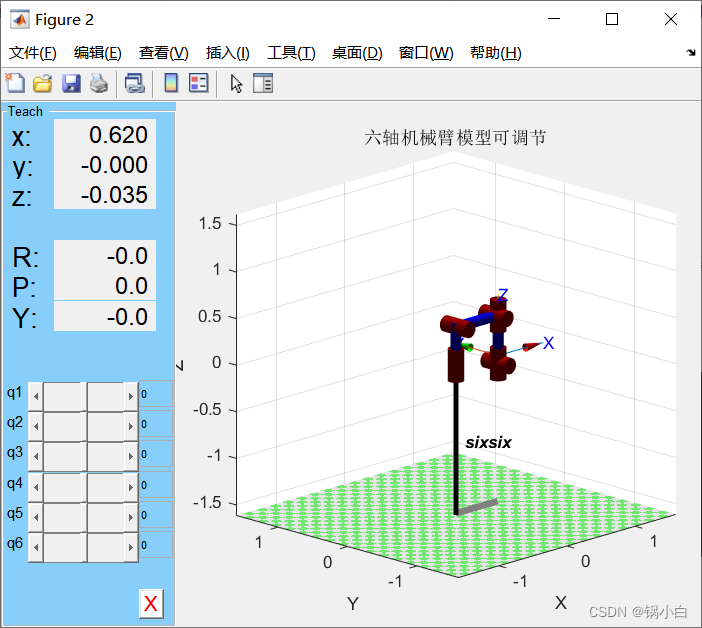
运行结果如上图所示,可以通过拖动各个关节q的进度条,观察不同关节角度下的机械臂位姿。
2 基于运动学求解的轨迹规划
正逆运动学求解
对于机械臂 robot0 = SerialLink(L,'name','six');
正运动学:robot0.fkine():输入期望的关节角度,输出末端齐次变换矩阵。
逆运动学:robot0.ikine()【仅用在标准型D-H建模方法中】:输入末端执行的齐次变换矩阵,输出得到的关节角度。
举例2:正运动学求解及轨迹实现
%% 已知机械臂初始和目标的关节角度,利用五次多项式进行轨迹规划robot0 = SerialLink(L,'name','six');T1=transl(0.5,0,0);%根据给定起始点,得到起始点位姿T2=transl(0,0.5,0);%根据给定终止点,得到终止点位姿init_ang=robot0.ikine(T1);%根据起始点位姿,得到起始点关节角targ_ang=robot0.ikine(T2);%根据终止点位姿,得到终止点关节角step = 20;%轨迹规划方法figure(3)%关节空间轨迹规划[q ,qd, qdd]=jtraj(init_ang,targ_ang,step); %五次多项式轨迹,得到关节角度,角速度,角加速度,20为采样点个数grid onT=robot0.fkine(q);%根据插值,得到末端执行器位姿nT=T.T;plot3(squeeze(nT(1,4,:)),squeeze(nT(2,4,:)),squeeze(nT(3,4,:)));%输出末端轨迹title('根据运动学求正解得到目标轨迹');robot0.plot(q);%动画演示 %% 求解上述运行过程中的位置、速度、加速度的变化曲线figure(4)subplot(3,2,[1,3]); %subplot 对画面分区 三行两列 占用1到3的位置plot3(squeeze(nT(1,4,:)),squeeze(nT(2,4,:)),squeeze(nT(3,4,:)));%输出末端轨迹robot2.plot(q);%动画演示figure(f)subplot(3, 2, 2);i = 1:6;plot(q(:,1));title('位置');grid on;figure(f)subplot(3, 2, 4);i = 1:6;plot(qd(:,1));title('速度');grid on;figure(f)subplot(3, 2, 6);i = 1:6;plot(qdd(:,1));title('加速度');grid on;得到的运行结果:
机械臂正解求解并轨迹运行
3 基于Solidworks和Matlab 的自定义机械臂模型的导入及使用
参考学习了视频三维模型_哔哩哔哩_bilibili(感谢up!!模型也是下载的up主的,视频讲解的很详细~),以四轴机械臂为例,在Solidworks中将每一个关节依次导出为STL格式的文件,具体步骤如下:
将Solidworks模型导入Matlab
1)下载三维模型【文件夹Fdof】(2条消息) 四轴机械臂三维模型(各Link零件及4DOFmanipulator装配体)资源-CSDN文库,并在Solidworks中打开装配体4DOFmanipulator.sldasm。
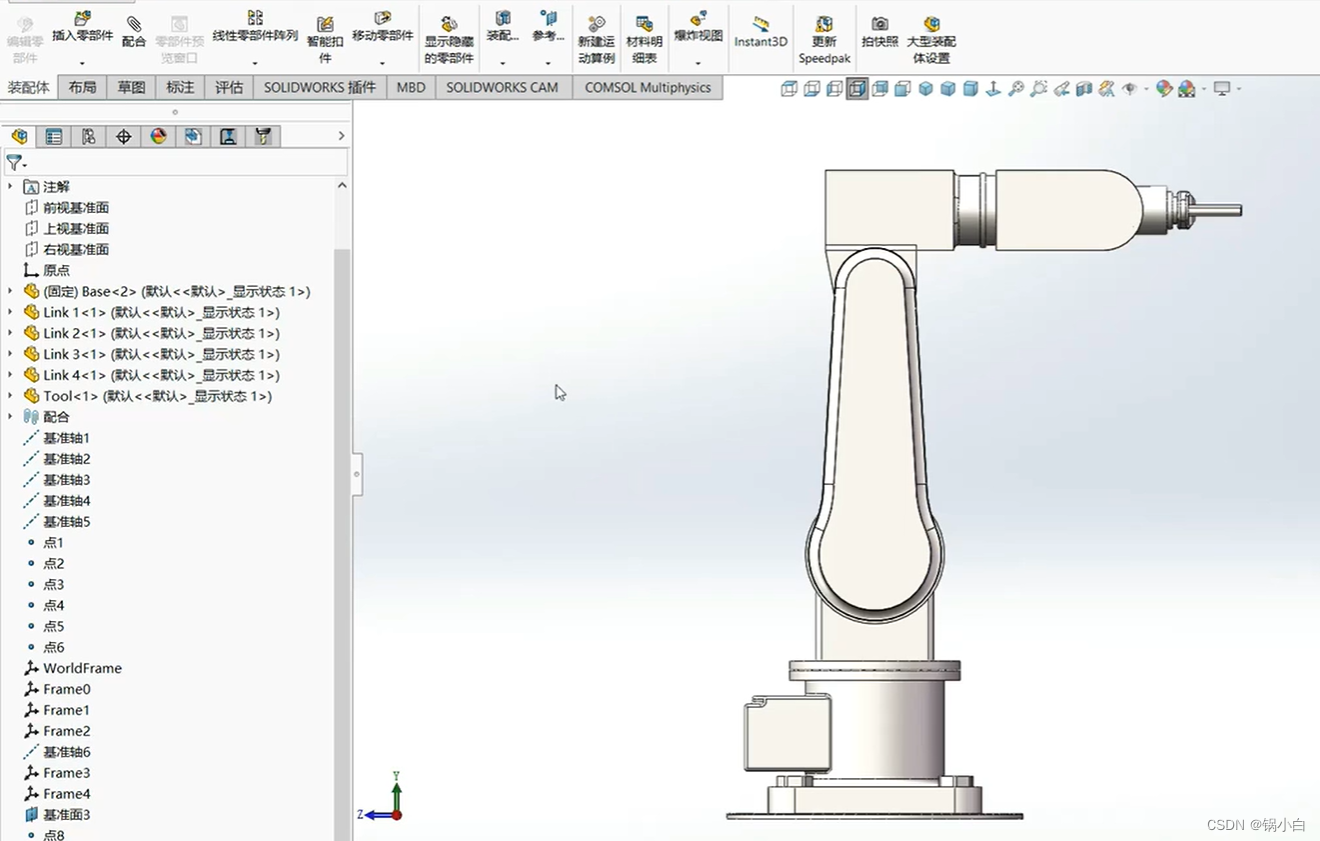
2)导出基座Base为 link0.STL 文件,另存为的路径选择刚刚下载的文件夹Fdof的路径。

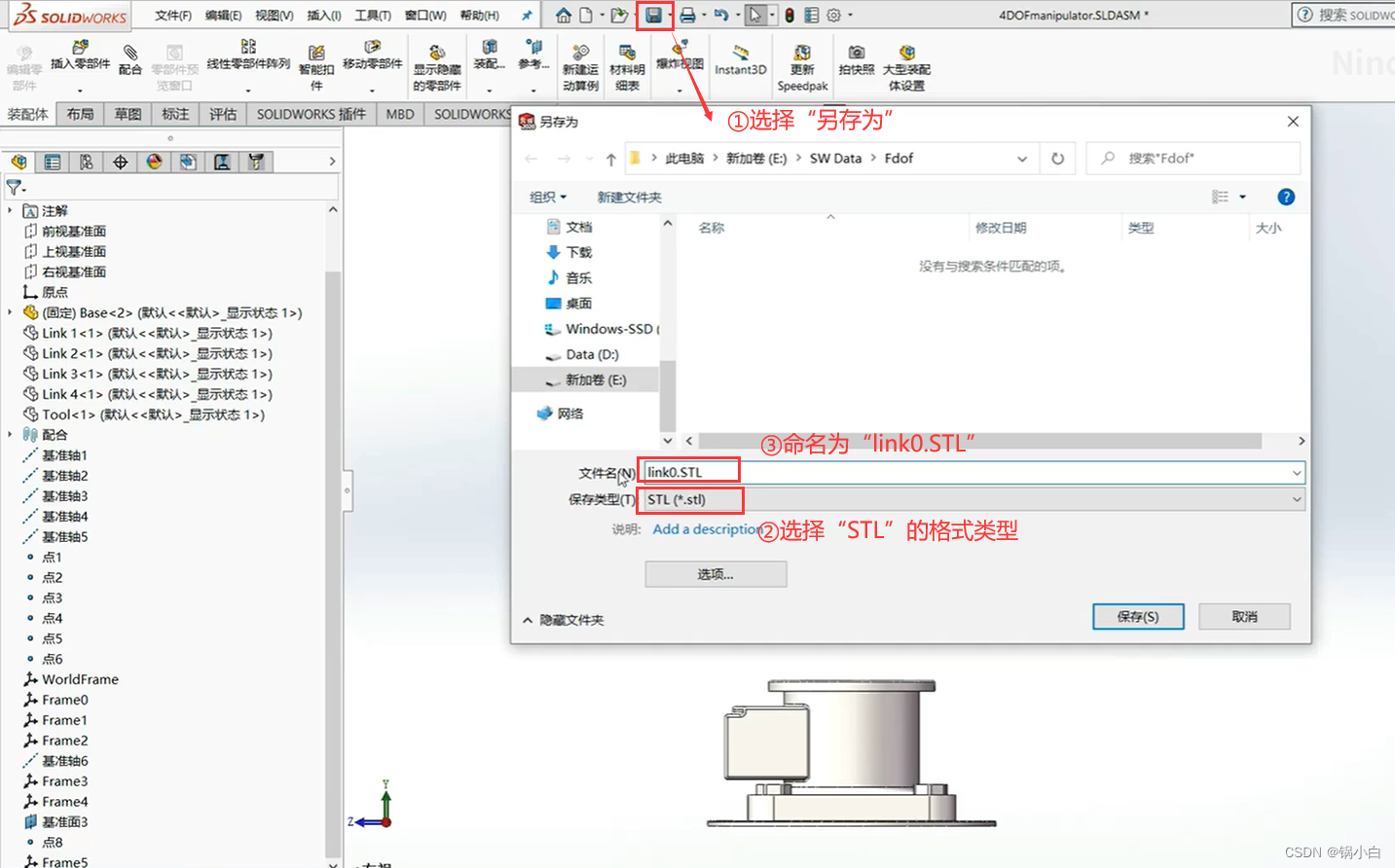
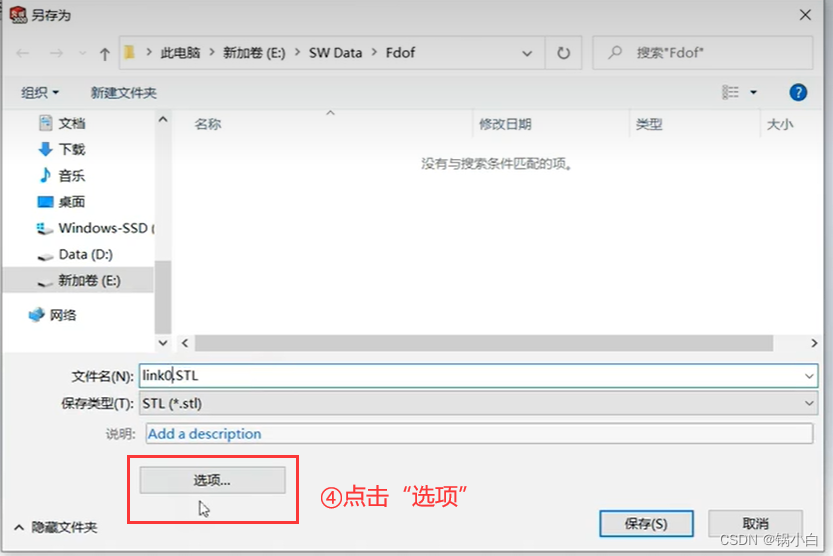
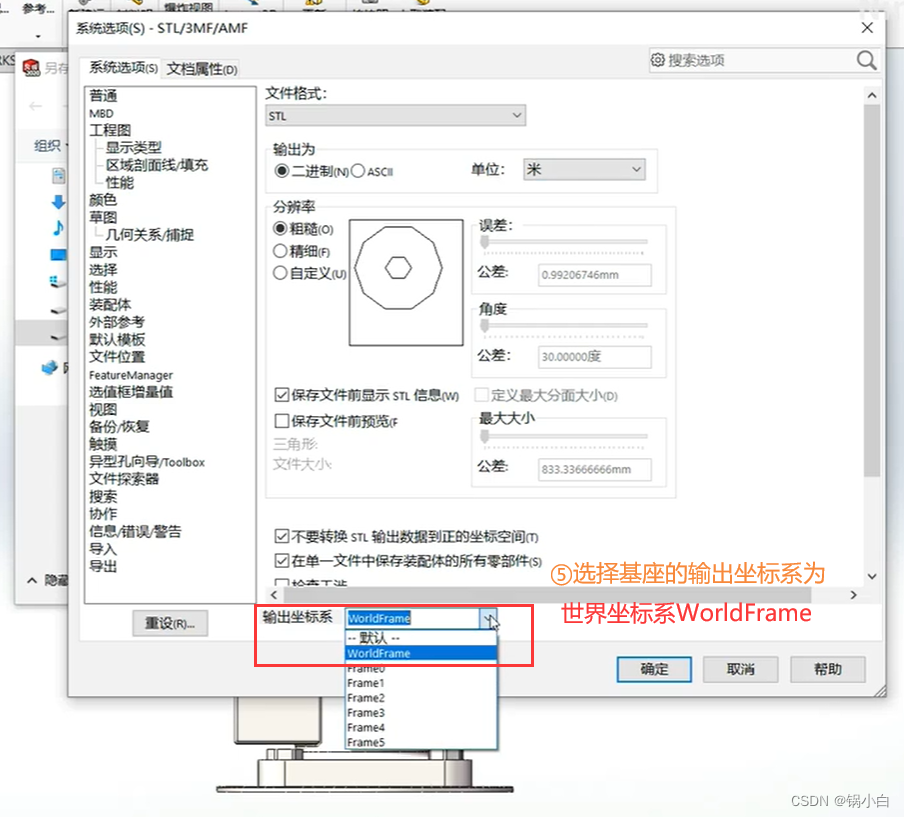
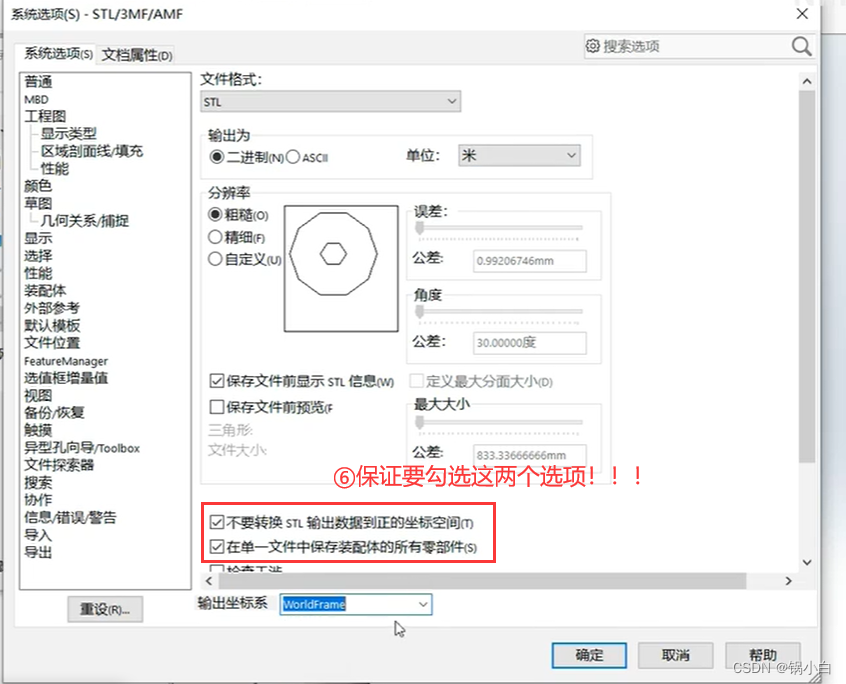
【注意:下面所有零件在导出至STL时都要勾选“不要转换STL输出到整的坐标空间”和“在单一文件中保存装配体的所有零部件”两个选项,否则会遇到导出到Matlab中时,零部件分离的情况】
3)导出第一个关节Link1为 link1.STL 文件


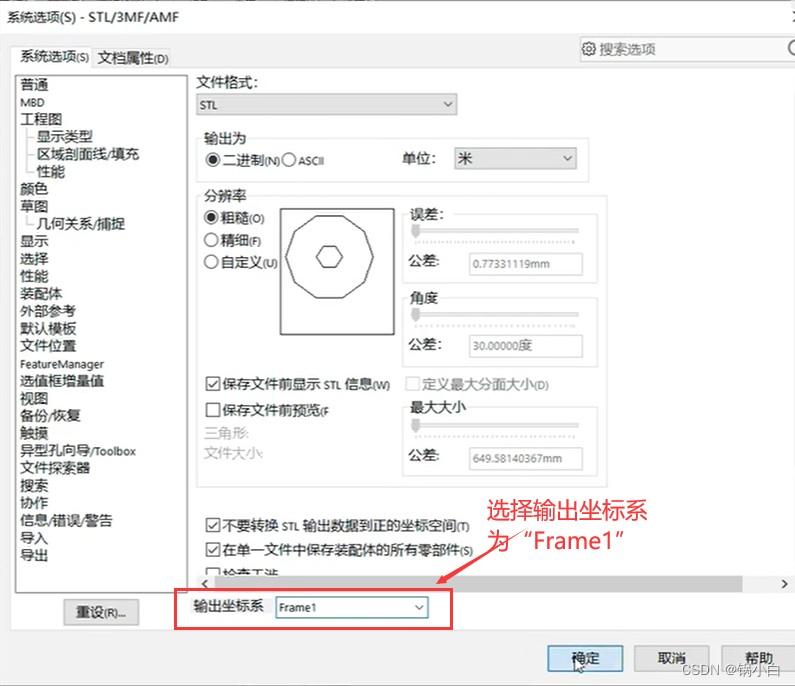
4)导出第二个关节Link2为 link2.STL 文件
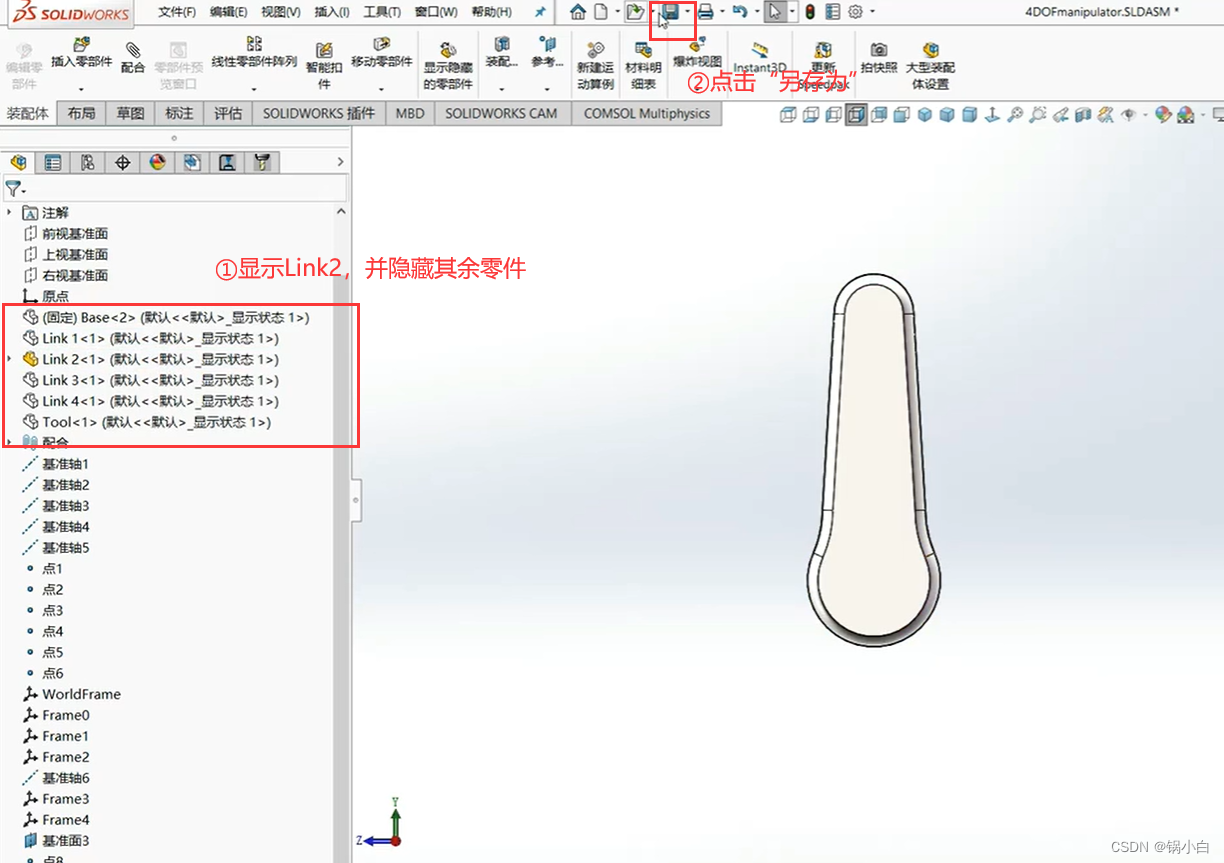
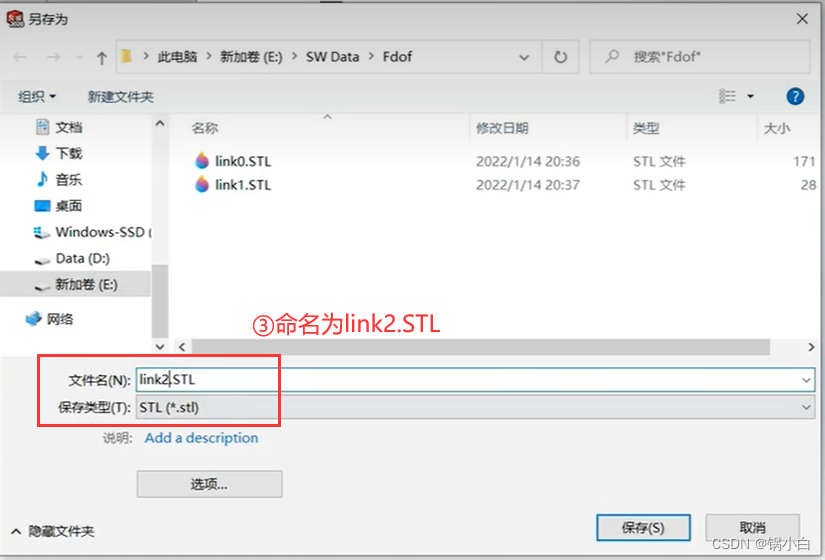
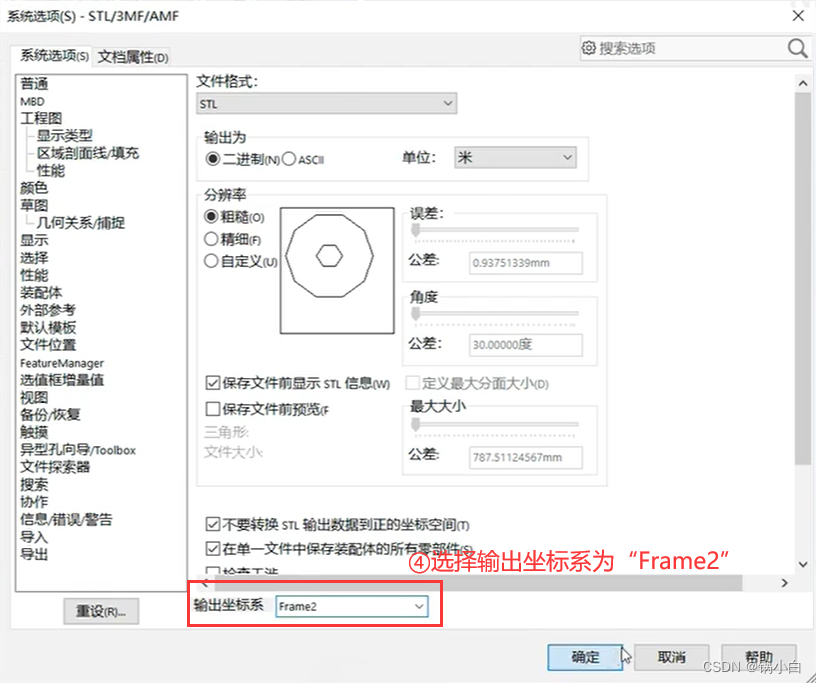
5)同理,导出第三个关节Link3为 link3.STL 文件,输出坐标系为Frame3;
导出第四个关节Link4为 link4.STL 文件,输出坐标系为Frame4;
导出工具Tool为 link5.STL 文件,输出坐标系为Frame5;
最终得到的文件夹Fdof中存在的文件有:
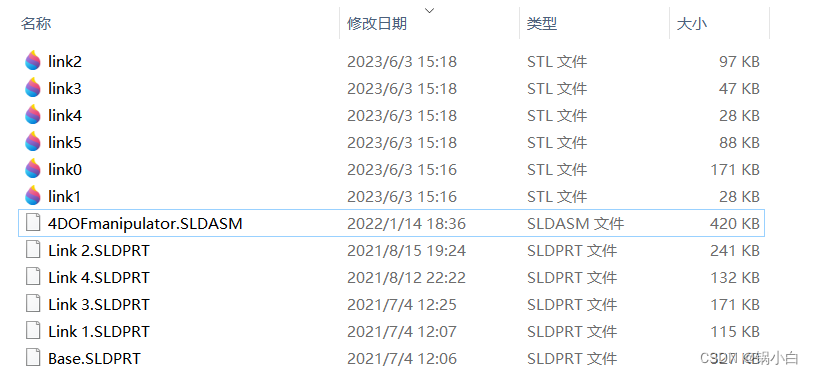
6)根据Solidworks建模时的物理参数大小,在Matlab中设置Link函数的参数值(关节转角θ,关节距离d,连杆长度a,连杆转角α),在Matlab中导入上述STL模型的代码如下:
举例3:自定义机械臂三维模型的Matlab运动学求解
clear;clc;L(1) = Link('revolute','d',0.216,'a',0,'alpha',pi/2);L(2) = Link('revolute','d',0,'a',0.5,'alpha',0,'offset',pi/2);L(3) = Link('revolute','d',0,'a',sqrt(0.145^2+0.42726^2),'alpha',0,'offset',-atan(427.46/145));L(4) = Link('revolute','d',0,'a',0,'alpha',pi/2,'offset',atan(427.46/145));L(5) = Link('revolute','d',0.258,'a',0,'alpha',0);Five_dof = SerialLink(L,'name','4-dof');Five_dof.base = transl(0,0,0.28); % 相当于将link1的frame1向上提升0.28(基座的高度),将机械臂放置在基座上q0 = [0 0 0 0 0];view = [35 20]; %plot函数的展示视角【方位角,仰角】w = [-1 1 -1 1 0 2]; %工作空间% 变量path的值'D:\Matlab2022a\...\Fdof','nowrist'仅为示意,改为自己的文件夹Fdof的路径Five_dof.plot3d(q0,'tilesize',0.1,'workspace',w,'path','D:\Matlab2022a\...\Fdof','nowrist','view',view)L1 = light('Position',[1 1 1],'color','w'); %加光源得到的运行结果为:
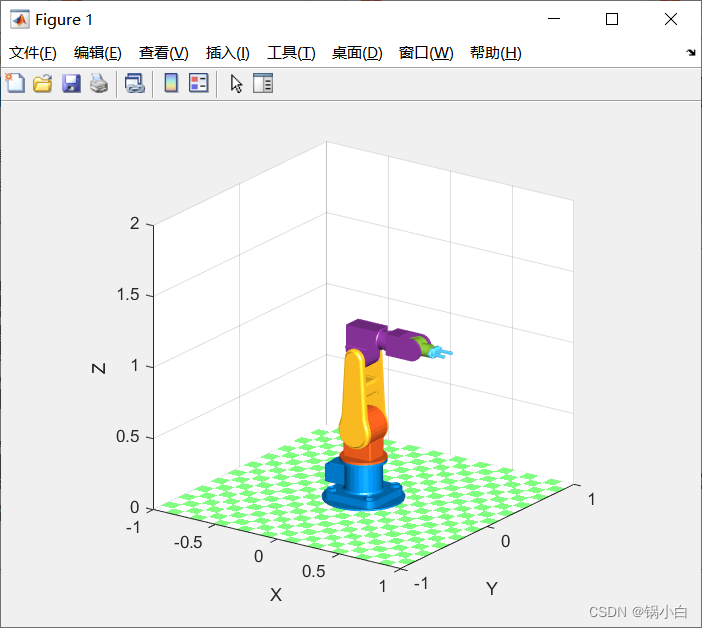
进行正运动学轨迹规划
接续上一段代码继续执行:
%% 给定目标位置为(0.5,0.5,0.5)机械臂求解正运动学的解并运动到该位置Position = [0.5 0.5 0.5];T1 = transl(Position)*rpy2tr(180,0,0); % 机械臂到达的末端位置(rpy2tr:Roll-pitch-yaw angles to SE(3) homogeneous transform)q1 = Five_dof.ikunc(T1); % 末端机械臂的关节位姿q = jtraj(q0,q1,60); % 计算从q0到q1的关节空间轨迹,T=60为时间(60帧)Five_dof.plot3d(q,'view',view,'fps',60,'nowrist'); % 'nowrist'表示绘制末端的坐标系