目录
AVL 树
a. AVL树的实现
(一)树的构建
(二)树的插入
AVL 树
AVL 树又叫平衡二叉树,它也有搜索二叉树的性质,但是:当向二叉搜索树中插入新结点后,能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度
a. AVL树的实现
(一)树的构建
代码
template<class K>struct node{node(const K& t){s = t;}node* left = nullptr;node* right = nullptr;node* parent = nullptr;K s;int _bf = 0;};// _bf 是平衡因子,记录左右子树之差,这里我们用 右子树高度 - 左子树高度
// parent 记录它们的父节点
(二)树的插入
实现原理和思路
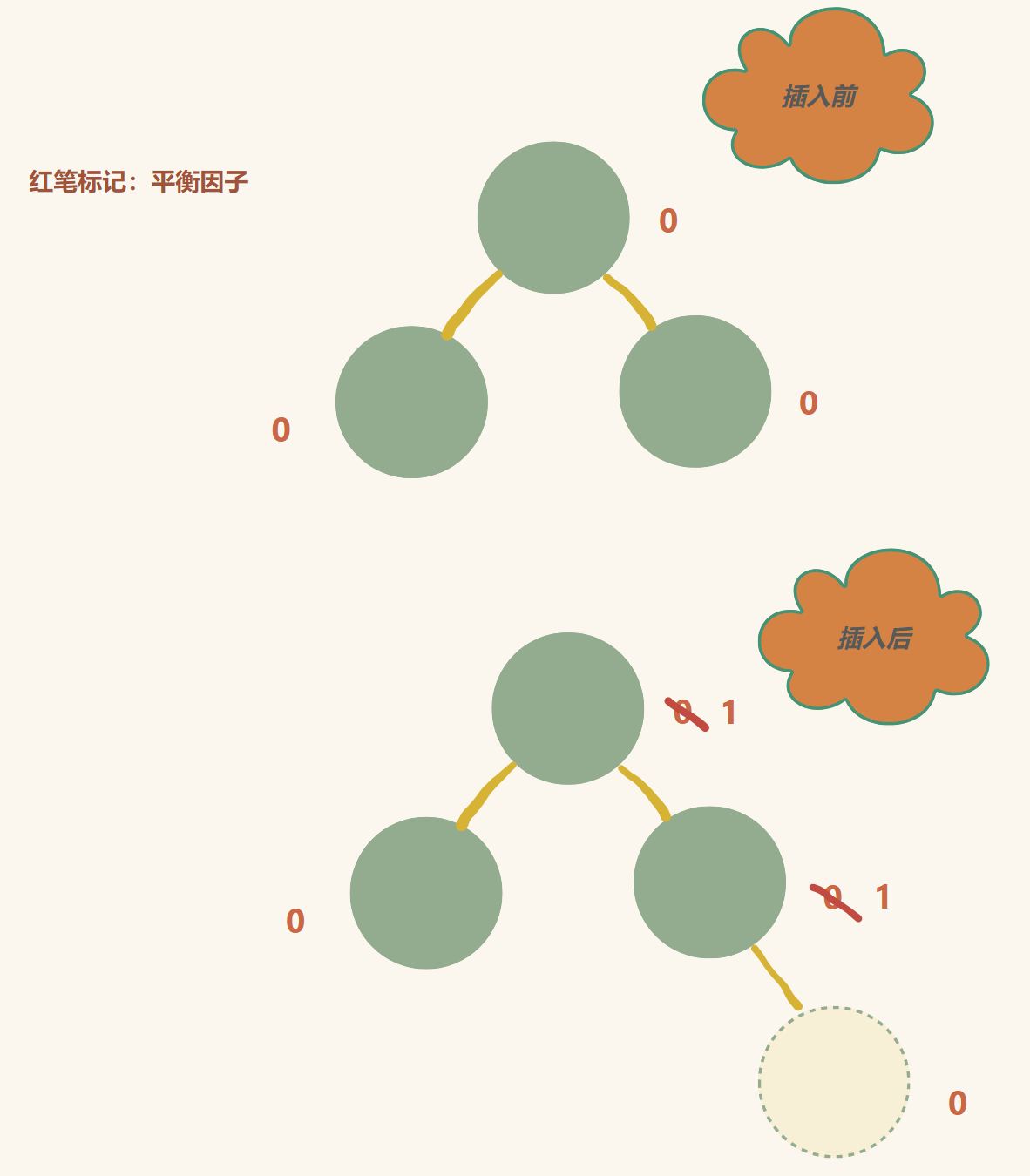
插入前半部分和搜索二叉树一样,但是在插入时,时刻更新每个节点的平衡因子,和每个节点的父节点,如果向某个父节点插入右子树,则平衡因子++,插入左子树,平衡因子--(这里实现的平衡因子是 右子树高度 - 左子树高度)
插入一个节点后,影响的不只是父节点的平衡因子,还有可能是父节点的父节点的平衡因子
因此,平衡因子有三种可能:
如果父节点的平衡因子是 -1 或者 1则父节点的原来的平衡因子是 0 (左右子树平衡),而现在平衡被破坏,则它的父节点的平衡因子也要更改(所以我们需要向上更改父节点的平衡因子,直到父节点为空,或者平衡因子不属于这一种情况)
如果父节点的平衡因子是 0
则现在的树已经平衡了,也不会影响它的父节点的平衡因子,不做任何处理,直接 break
如果父节点的平衡因子是 2 或者 - 2则此时AVL树要保持左右子树一定高度(发生旋转)
代码大框架(里层实现没有完成)
template<class K>class bin_node{public:typedef node<K> Node;bool insert(K & t){if (_root == nullptr){_root = new Node(t);return true;}Node* _parent = _root;Node* cur = _root;while (cur){if (cur->s > t){_parent = cur;cur = cur->left;}else if (cur->s < t){_parent = cur;cur = cur->right;}else{return false;}}cur = new Node(t);if (cur->s > _parent->s){cur->parent = _parent;_parent->right = cur;_parent->_bf++;}else{cur->parent = _parent;_parent->left = cur;_parent->_bf--;}while (_parent){if (_parent->_bf == 1 || _parent->_bf == -1){cur = _parent;_parent = _parent->parent;if (_parent){if (_parent->s > cur->s){_parent->_bf--;}else{_parent->_bf++;}}}else if (_parent->_bf == 2 || _parent->_bf == -2){ //旋转(代码实现在后面)}else if(_parent->_bf == 0){break;}else{assert(false);}}return true;}private:Node* _root = nullptr;};
旋转原理
探讨什么时候发生旋转
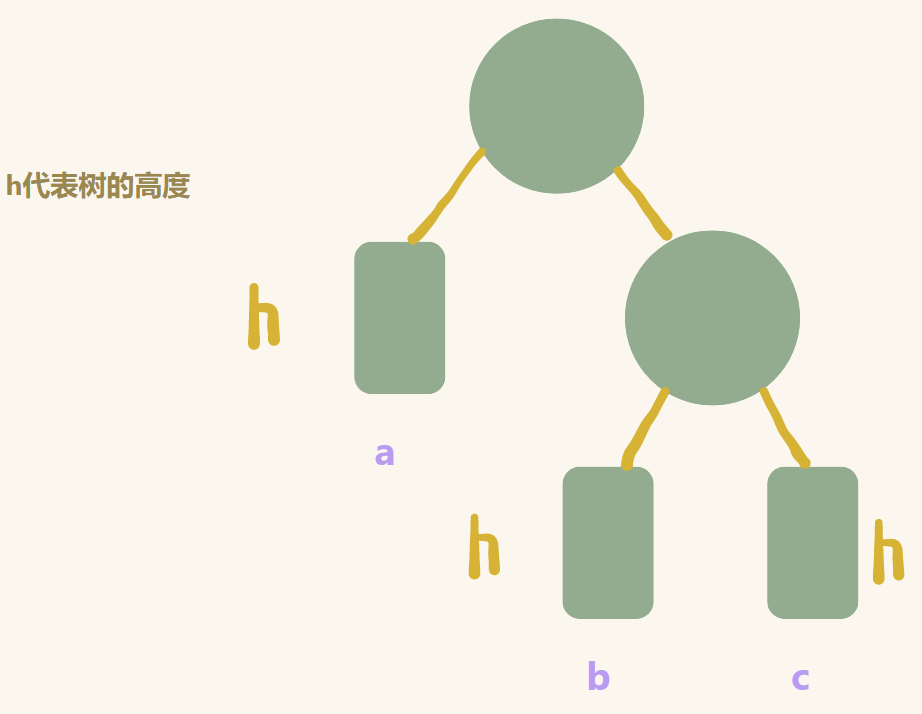
第一种情况
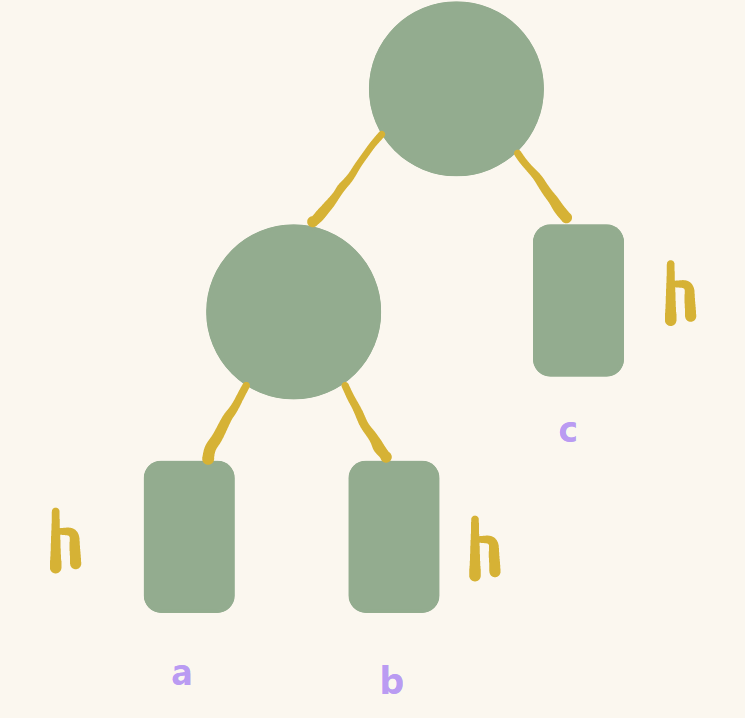
2. 第二种情况
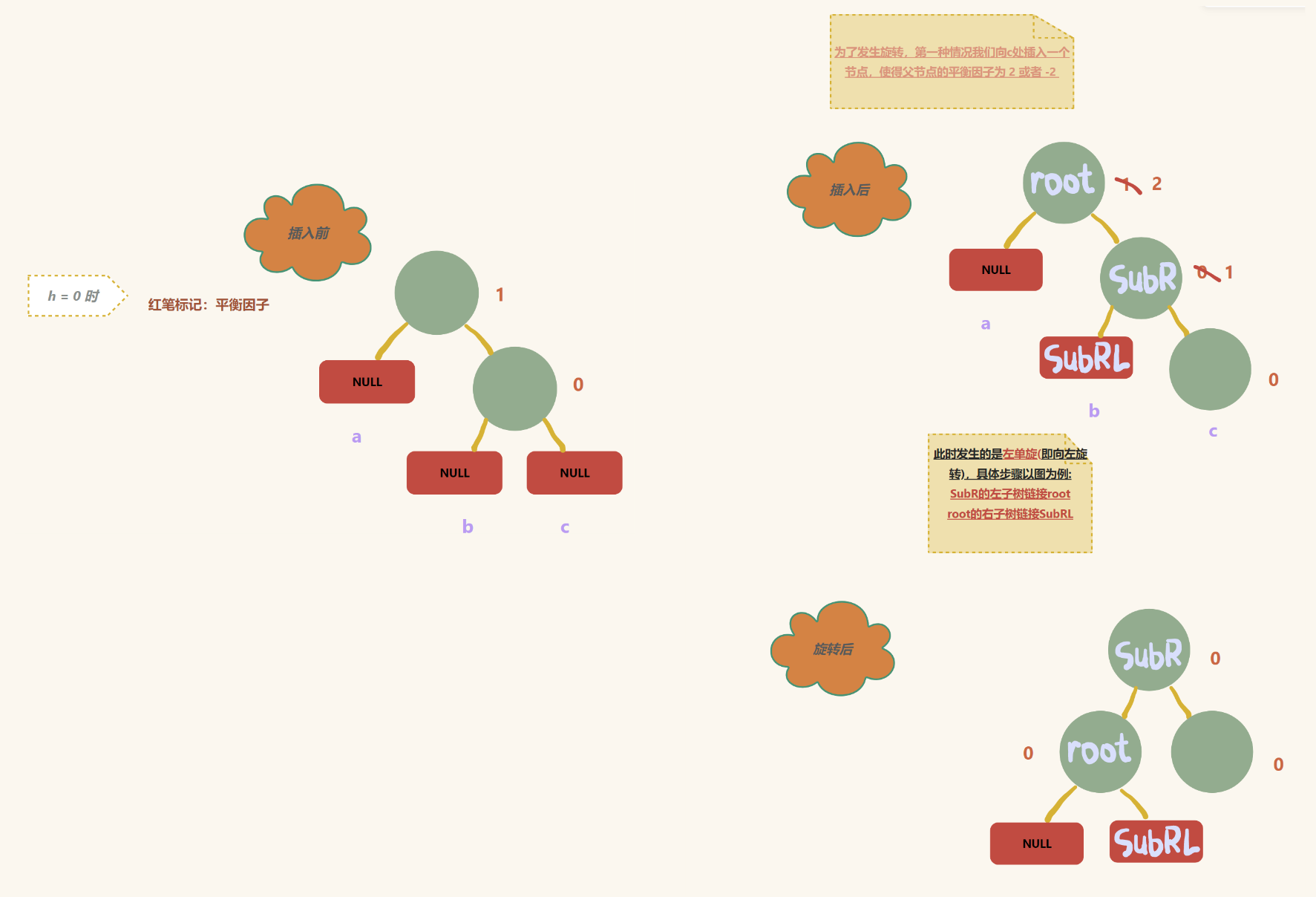
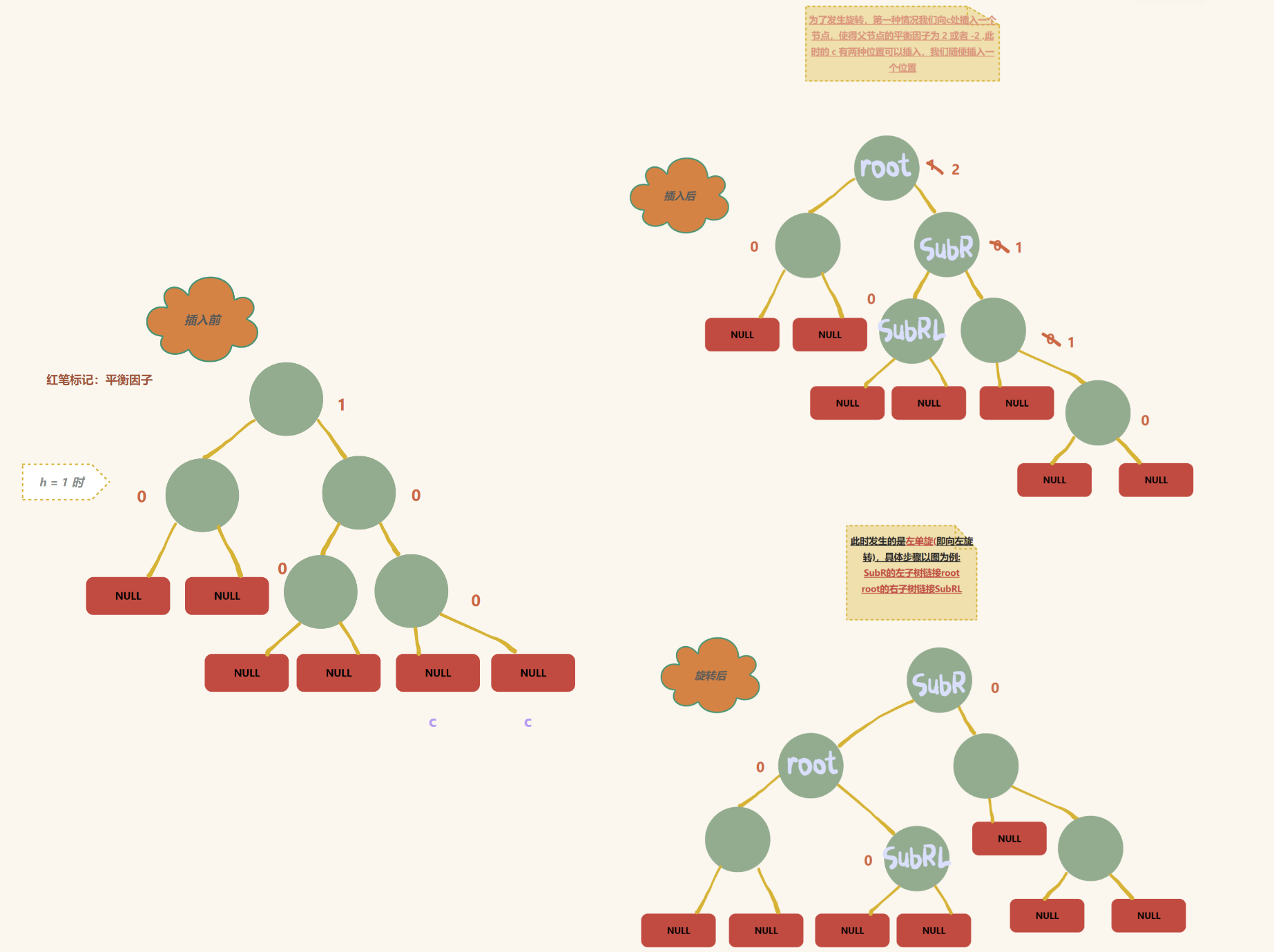
针对第一种情况,举几个示例再细分一下:(向 c 插入节点)
综上:
左单旋:SubR的左子树链接root,root的右子树链接SubRL
我们容易发现,对于发生左单旋的树,root , SubR ,SubRL 的平衡因子都是 0
发生这个场景, root 的平衡因子是 2 ,SubR 的平衡因子是 1
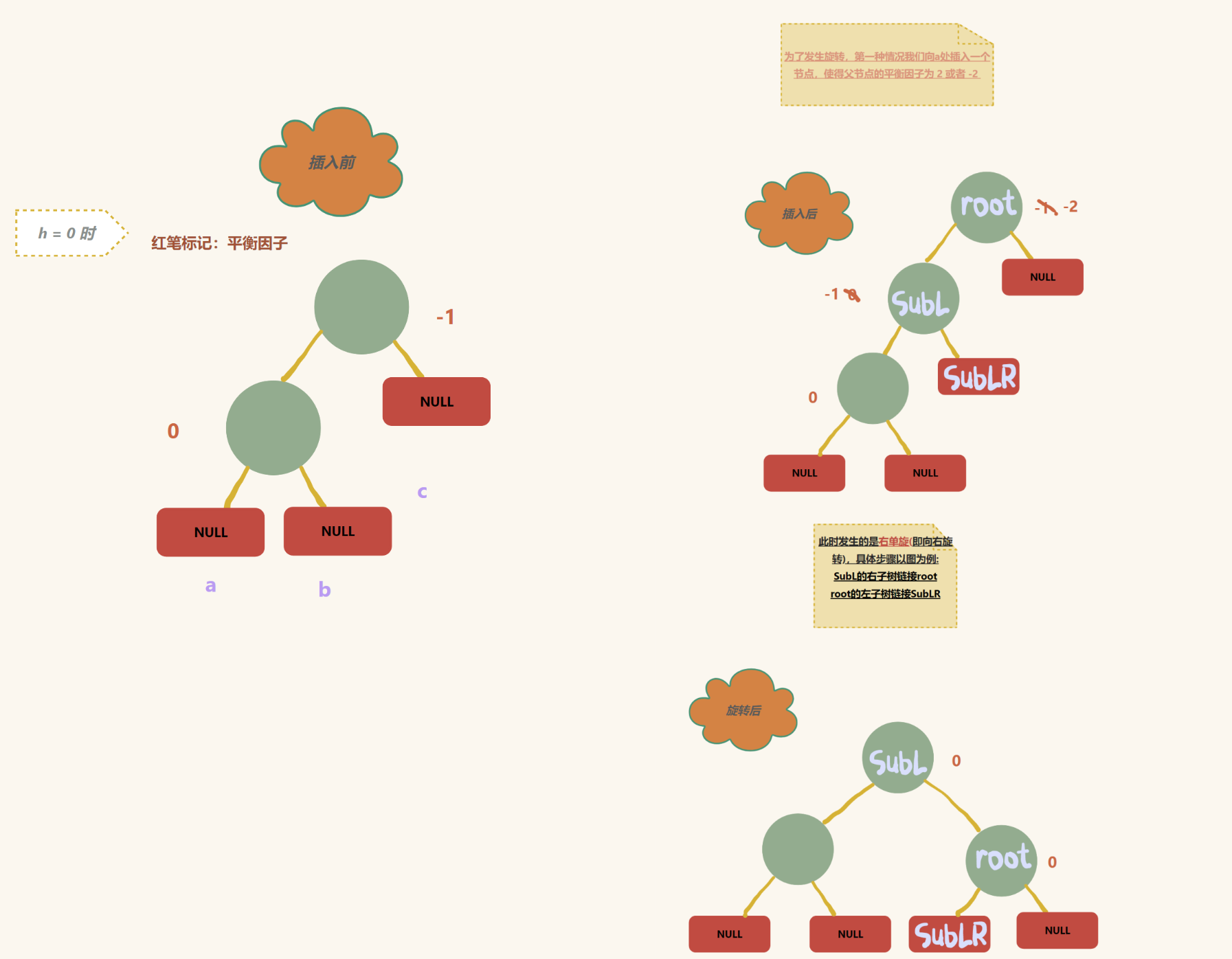
针对第二种情况:(向 a 插入节点)
综上:
SubL的右子树链接root , root的左子树链接SubLR
我们容易发现,对于发生左单旋的树,root , SubL ,SubLR 的平衡因子都是 0
发生这个场景, root 的平衡因子是 -2 ,SubL 的平衡因子是 -1
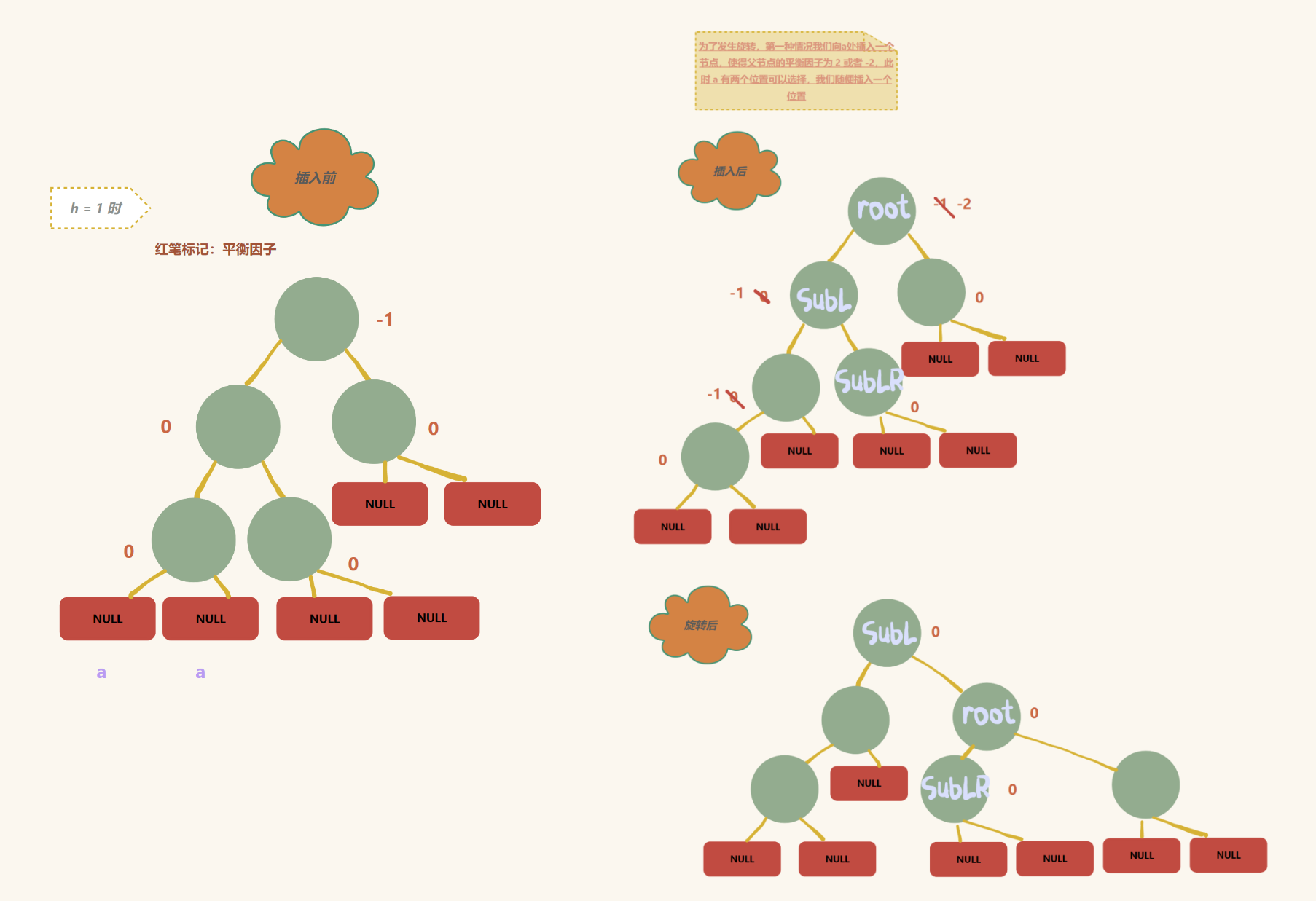
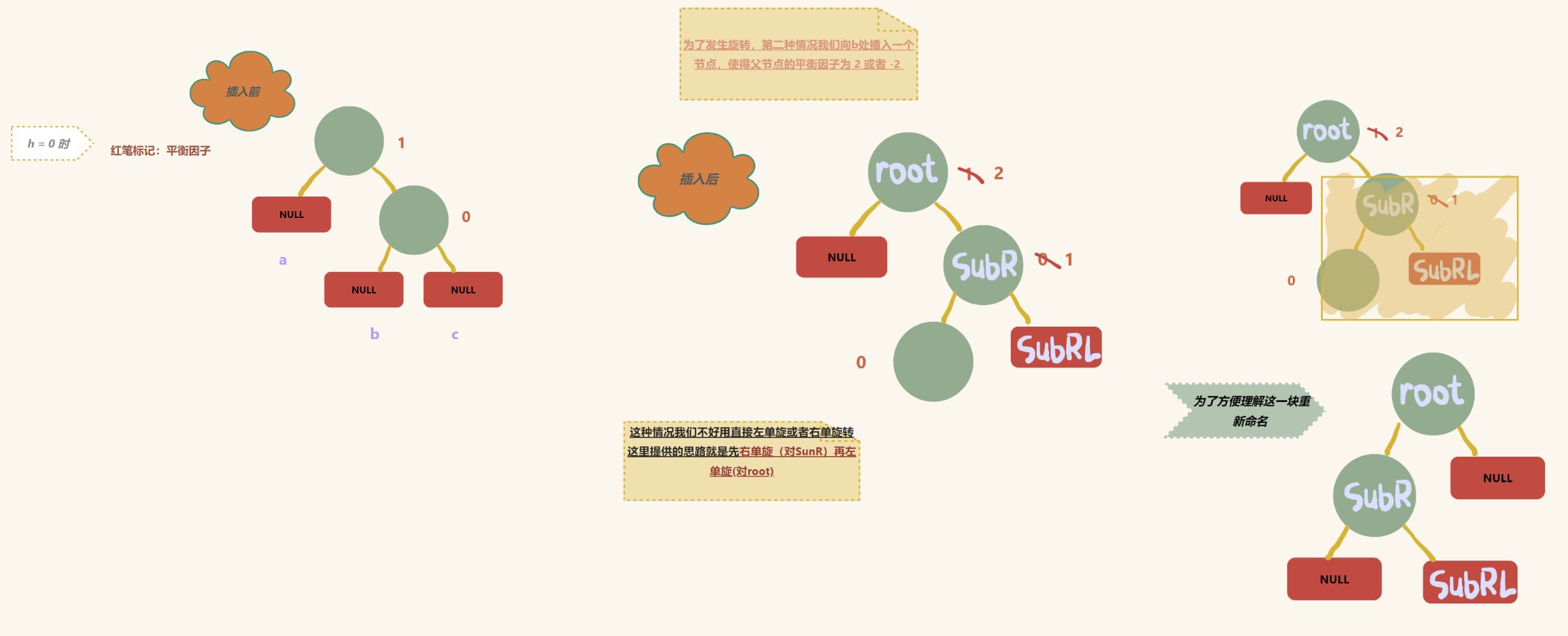
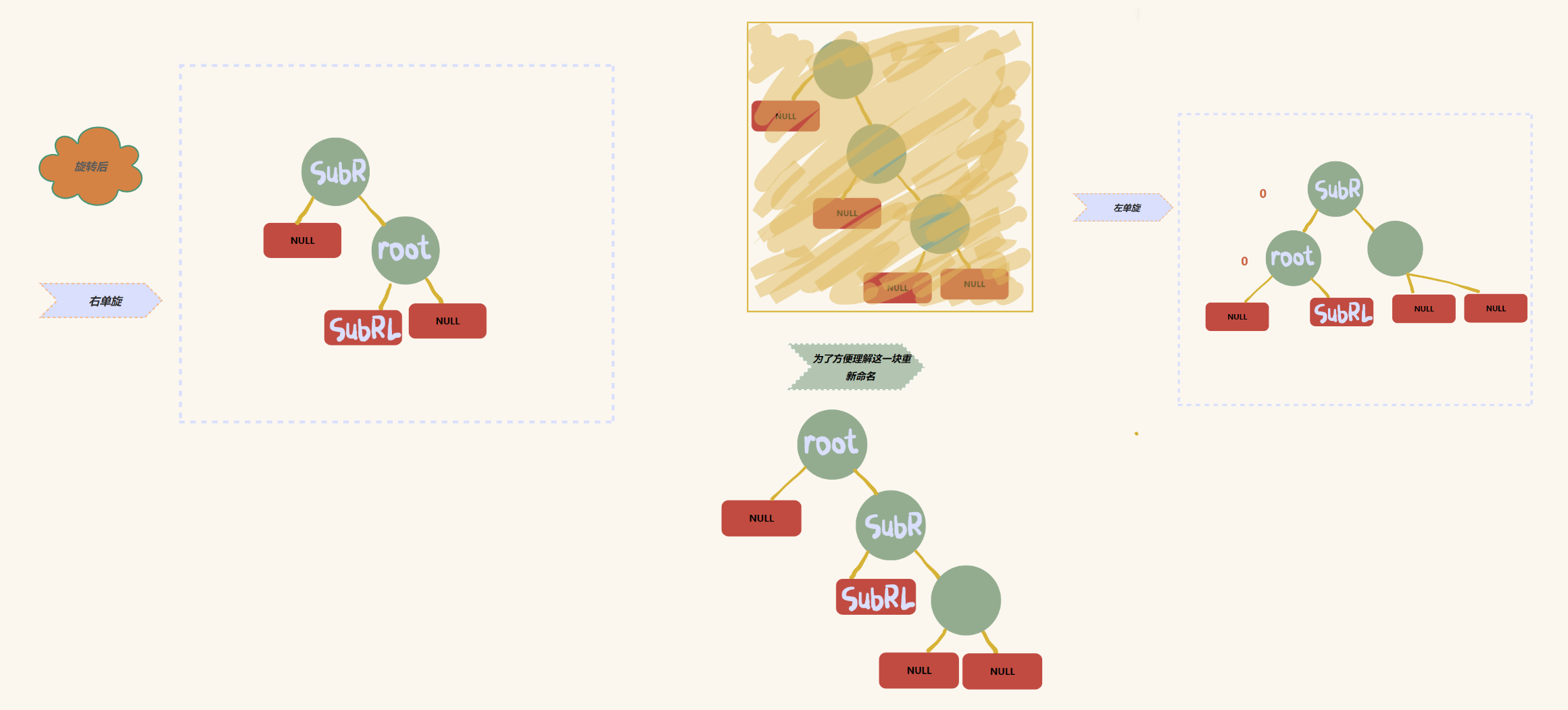
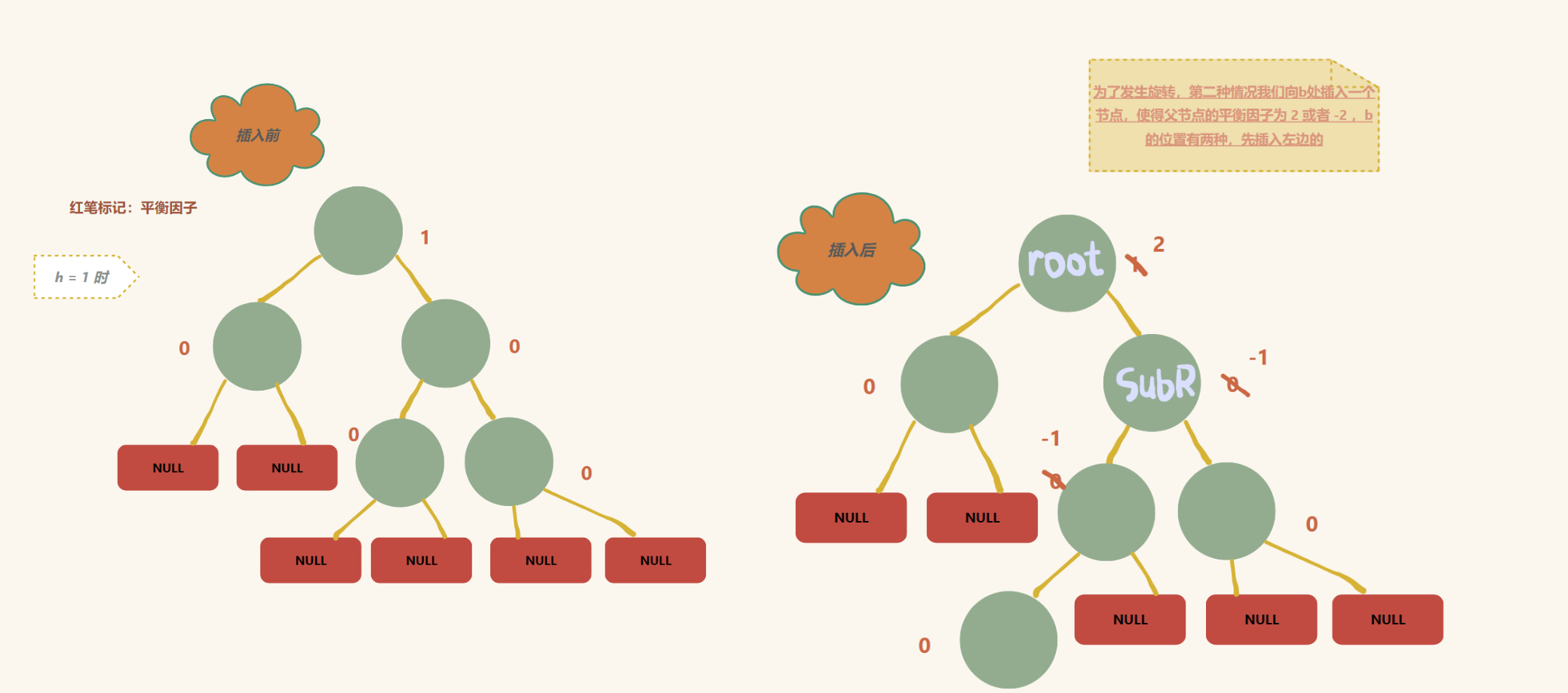
回到第一种情况:(向 b 插入节点)
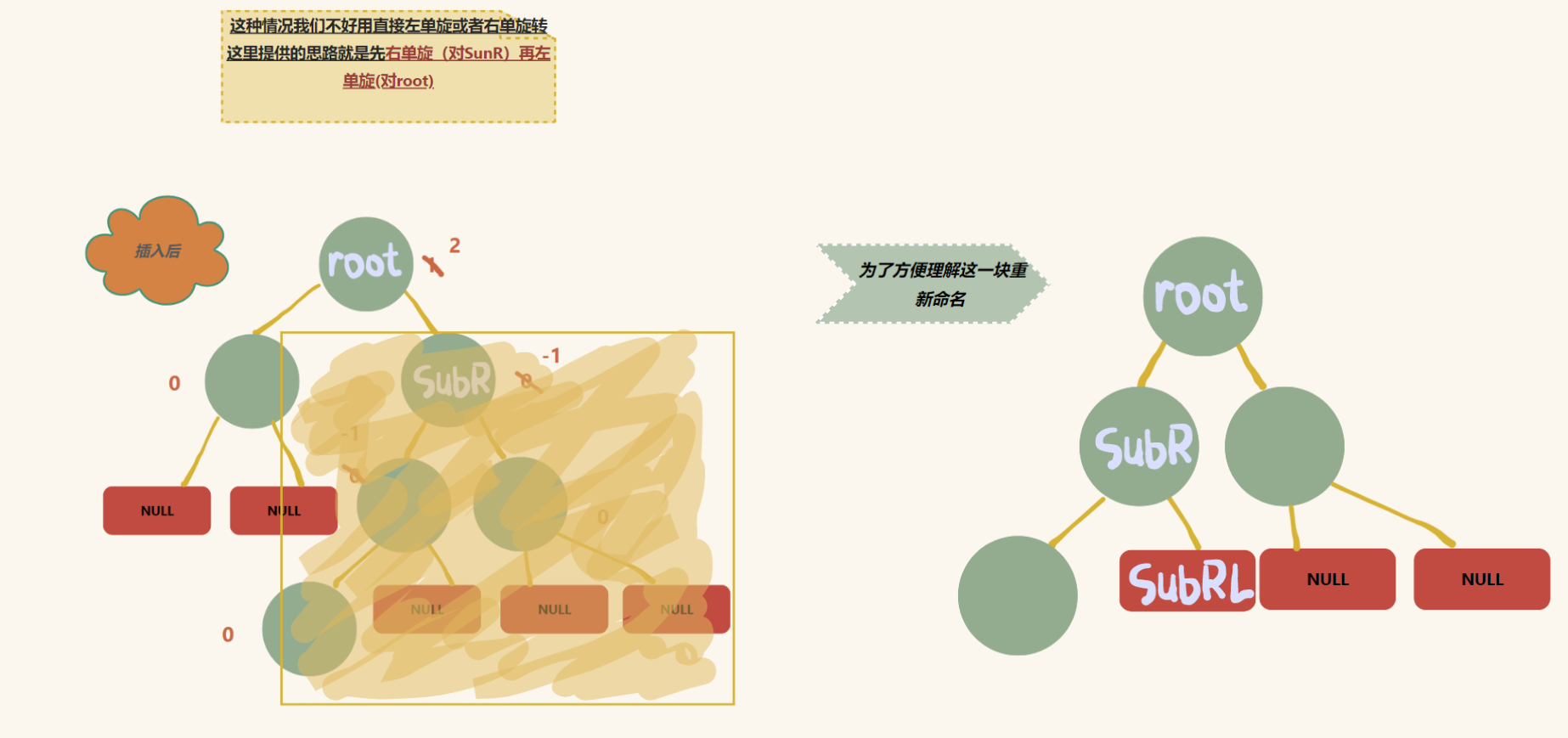
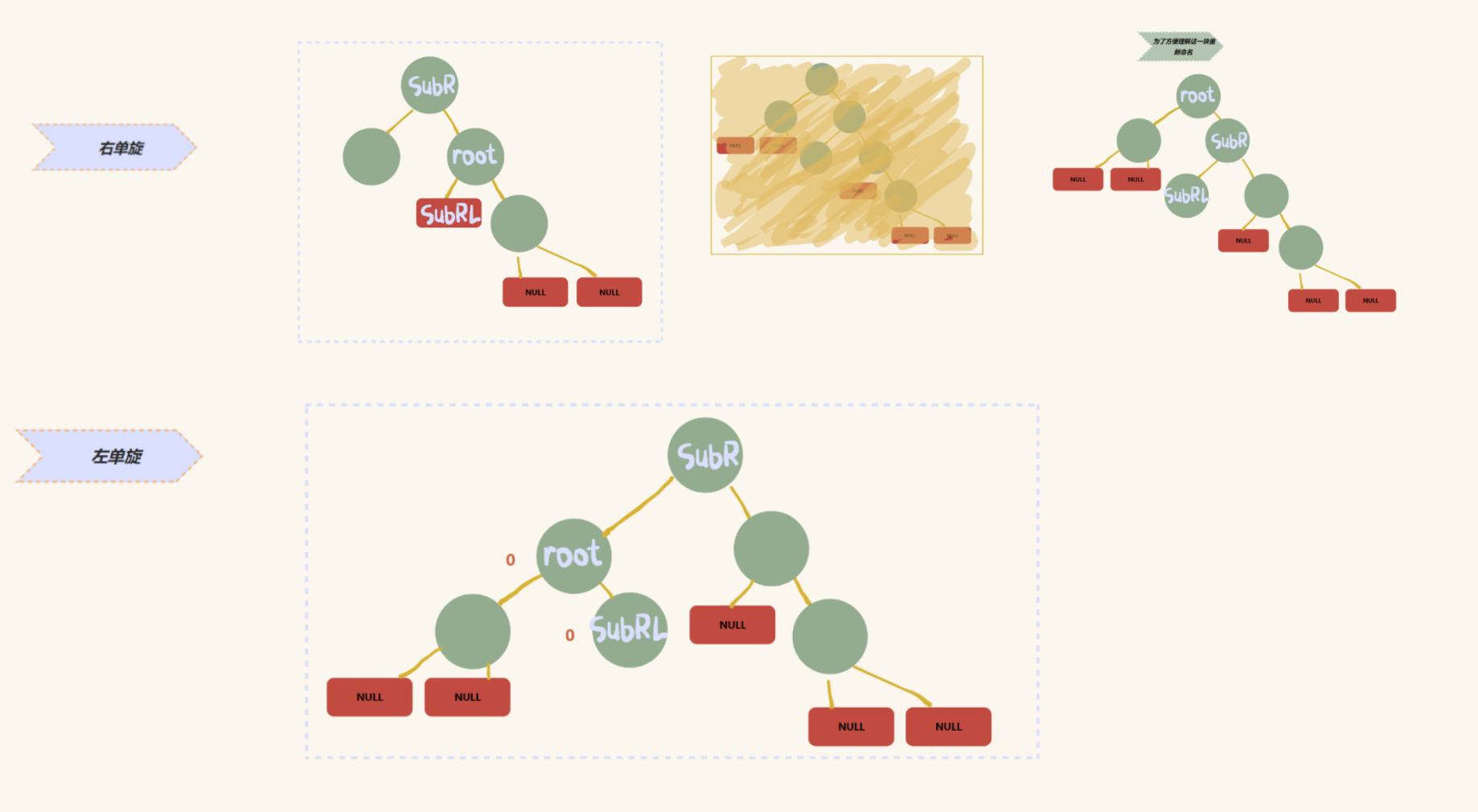
综上:
先右单旋,再左单旋
此情况发生在 root 的平衡因子为 2 ,SubR的平衡因子为 - 1
其它的情况照例分析即可(如 h = 1 是 ,插入是右子树)
回到第二种情况(向 b 插入节点)
同理可得: 先左单旋,再右单旋
此情况发生在 root 的平衡因子为 -2 ,SubR的平衡因子为 1
注意:
注意 根节点特殊情况 和 节点之间的相连(尤其是父节点的链接)平衡因子的修改最好举例画图
完整代码
template<class K>struct node{node(const K& t){s = t;}node* left = nullptr;node* right = nullptr;node* parent = nullptr;K s;int _bf = 0;};template<class K>class bin_node{public:typedef node<K> Node;bool insert(K & t){if (_root == nullptr){_root = new Node(t);return true;}Node* _parent = _root;Node* cur = _root;while (cur){if (cur->s > t){_parent = cur;cur = cur->left;}else if (cur->s < t){_parent = cur;cur = cur->right;}else{return false;}}cur = new Node(t);if (cur->s > _parent->s){cur->parent = _parent;_parent->right = cur;_parent->_bf++;}else{cur->parent = _parent;_parent->left = cur;_parent->_bf--;}while (_parent){if (_parent->_bf == 1 || _parent->_bf == -1){cur = _parent;_parent = _parent->parent;if (_parent){if (_parent->s > cur->s){_parent->_bf--;}else{_parent->_bf++;}}}else if (_parent->_bf == 2 || _parent->_bf == -2)//旋转{if (_parent->_bf == 2){if (cur->_bf == 1){RotateR(_parent);break;}else if (cur->_bf == -1){RotateRL(_parent);}else{assert(false);}}else{if (cur->_bf == -1){RotateR(_parent);}else if (cur->_bf == 1){RotateLR(_parent);}else{assert(false);}}break;}else if(_parent->_bf == 0){break;}else{assert(false);}}return true;}void InOder(){_InOder(_root);}private:void _InOder(Node* root){if (root == nullptr){return;}_InOder(root->left);cout << root->s << " ";_InOder(root->right);}void RotateLR(Node* root) //左右旋转{Node* SubL = root->left;Node* SubLR = SubL->right;int n = SubLR->_bf;RotateL(SubL);RotateR(root);if (n == -1){SubL->_bf = 0;SubLR->_bf = 0;root->_bf = 1;}else if (n == 1){SubLR->_bf = 0;SubL->_bf = -1;root->_bf = 0;}else if (n == 0){SubLR->_bf = 0;SubL->_bf = 0;root->_bf = 0;}else{assert(false);}}void RotateRL(Node* root) //右左旋转{Node* SubR = root->right;Node* SubRL = SubR->left;int n = SubRL->_bf;RotateR(SubR);RotateL(root);if (n == -1){SubR->_bf = 1;SubRL->_bf = 0;root->_bf = 0;}else if (n == 1){SubRL->_bf = 0;SubR->_bf = 0;root->_bf = -1;}else if (n == 0){SubRL->_bf = 0;SubR->_bf = 0;root->_bf = 0;}else{assert(false);}}void RotateL(Node* root) //左单旋{Node* SubR = root->right;Node* SunRL = SubR->left;if (root == _root){_root = SubR;}else{Node* parent = root->parent;if (parent->left == root){parent->left = SubR;}else{parent->right = SubR;}}root->right = SunRL;SubR->left = root;SubR->parent = root->parent;root->parent = SubR;root->_bf = SubR->_bf = 0;}void RotateR(Node* root) //右单旋{Node* SubL = root->left;Node* SubLR = SubL->right;if (root == _root){_root = SubL;}else{Node* parent = root->parent;if (parent->left == root){parent->left = SubL;}else{parent->right = SubL;}}root->left = SubLR;SubL->right = root;SubL->parent = root->parent;root->parent = SubL;root->_bf = SubL->_bf = 0;}Node* _root = nullptr;};