♥♥♥♥♥个人主页♥♥♥♥♥
♥♥♥♥♥数据结构练习题总结专栏♥♥♥♥♥
文件目录
前言1.括号匹配1.1问题描述1.2解题思路1.3画图解释1.4代码实现2.逆波兰表达式求值 2.1问题描述2.2解题思路2.3画图解释2.4代码解释3.出栈入栈次序匹配 3.1问题描述3.2思路分析3.3画图解释3.4代码实现4.最小栈 4.1问题描述4.2思路分析4.3画图分析4.4代码实现
前言
在学习数据结构的过程中遇到了各种各样类型的题目,我在解答这些题目的时候收获了不少,所以我想开设一个专栏来分享我平时做题的收获,在我分享的题中我采用三步法来阐述,希望大家可以在我的文章有收获,并且能够在评论区中积极讨论更多的解题方法。
1.括号匹配
1.1问题描述
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
1.左括号必须用相同类型的右括号闭合。
2.左括号必须以正确的顺序闭合。
3.每个右括号都有一个对应的相同类型的左括号
1.2解题思路
大主题:我们先遍历这个字符串,在遇到左括号就进行压栈,遇到右括号则出栈并与左括号匹配,在这会出现两种情况:
1.如果不匹配,则直接返回false。
2.如果匹配,则可以继续去遍历这个字符串。
特殊情况:
1.当遍历完字符串,发现栈中还有元素,则可以直接返回false。
2.当栈中的元素已经全部被弹出,发现字符串没有被遍历完,也直接返回false。
1.3画图解释
1.大主题:
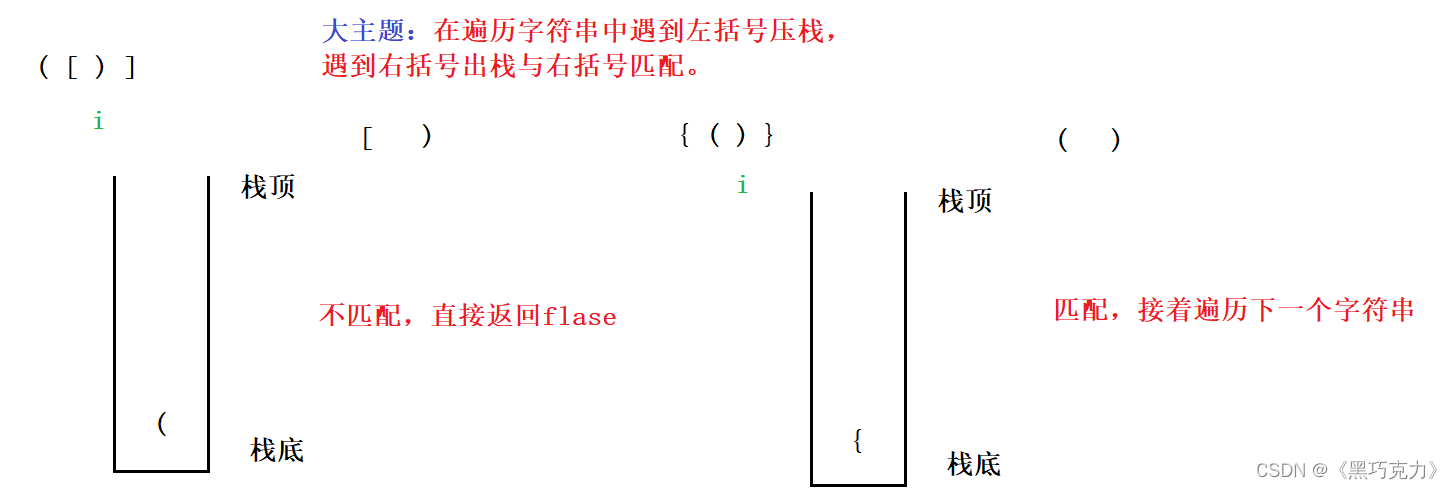
2.特殊情况:
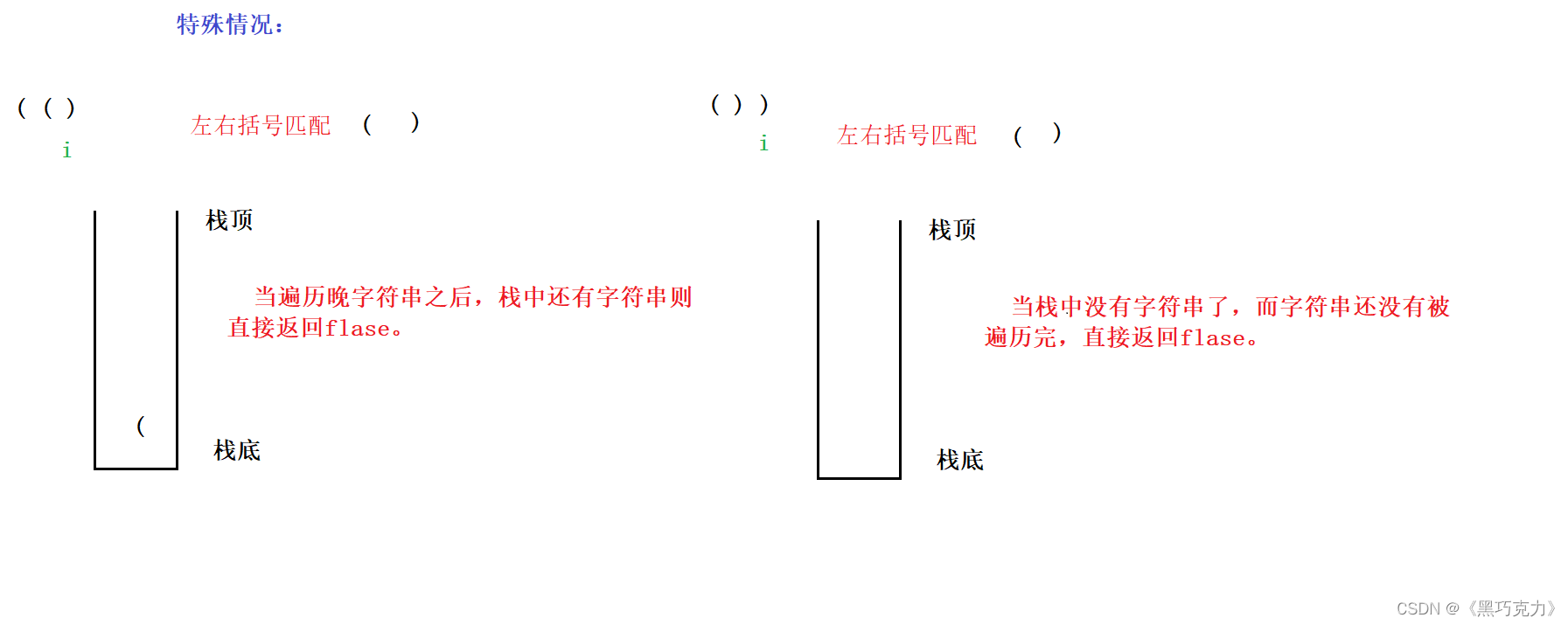
1.4代码实现
public class ParenMatch { Stack<Character> stack = new Stack<>(); public boolean isValid(String str) { //1.遍历这个数组 for (int i = 0; i < str.length(); i++) { //2.判断是左括号还是右括号 char ch = str.charAt(i); //2.1左括号 if(ch == '(' || ch == '[' || ch == '{' ) { //压栈 stack.push(ch); } //2.2右括号 看栈中是否为空,为空直接返回flase 不为空判断左右括号是否匹配。 else { //2.2.1栈中不为空 if(!stack.empty()) { char ch1 = stack.peek();//ch1是左括号。 //判断括号是否匹配 if(ch == ')' && ch1 == '(' || ch == ']' && ch1 == '[' || ch == '}' && ch1 == '{') { stack.pop(); } else { return false; } } //2.2.2栈中为空 else { return false; } } } //当数组遍历完之后,判断栈中是否空。 return stack.empty(); } public static void main(String[] args) { String str = "{()}"; ParenMatch parenMatch = new ParenMatch(); System.out.println(parenMatch.isValid(str)); }}2.逆波兰表达式求值
2.1问题描述
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
每个操作数(运算对象)都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。
2.2解题思路
在解决这个问题,我先解释什么叫逆波兰表达式,其实它有个更好理解的一个名字叫后缀表达式,我们既然提到了后缀表达式,那估计也有一些人不知道后缀表达式是什么?那我们就需要引出中缀表达式来了解后缀表达式。
其实中缀表达式就是我们平时经常可以见到的一个表达式,它就是将运算符放在数字之间的一种表达式如:a+(b+c)+d*(e+f)这种类型的就叫中缀表达式,而后缀表达式其实就是将运算符放在数字的后面。我就用a+(b+c)+d*(e+f)这个来打比方,将它转化为后缀表达式。
中缀表达式转后缀表达式分三步:
第一步:加括号,从左到右先乘除后加减去加括号。
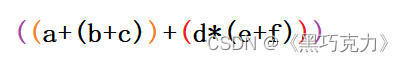
第二步:将运算符移到每个对应括号的外面
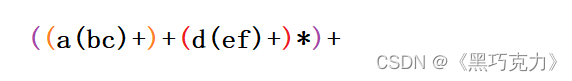
第三步:再将所有的括号全部删除,得到的就是后缀表达式
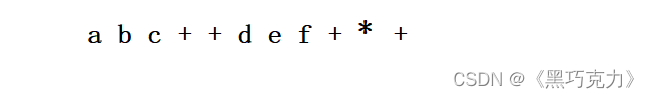
既然得到了后缀表达式,那我们运用栈来求这个表达式的值。
我们先将这个表达式看作一个字符串,然后我们再采用遍历的方法去一个一个的去遍历这个字符串,我采取的规则是遇到除运算符的任何元素压入栈中,遇到运算符则从栈中弹出两个元素,分别放在运算符的右侧和左侧(这里的左右很重要,因为运算符如果是除法或者减法,运算符的左右侧元素不同那么结果是不一样)得到的结果压入栈中,直到字符串遍历完之后,最后留在栈中的值就是这个表达式的值。
2.3画图解释
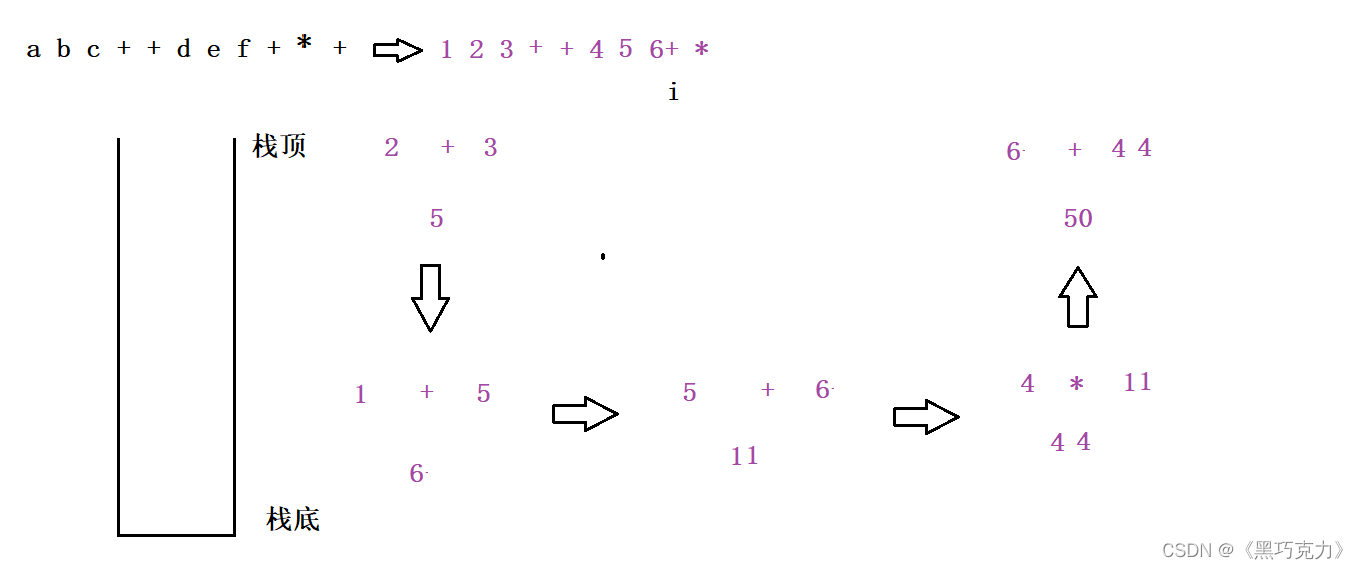
2.4代码解释
public class evalRPN { String[] tokens = {"2","1","+","3","*"}; Stack<Integer> stack = new Stack<>(); public int ergodic() { //遍历这个数组 for (int i = 0; i < tokens.length; i++) { //判断字符串是否为运算符字符串 String str = tokens[i]; if(!isOperator(str)) { //字符串为数字,说明将这个字符串数字先转化为数字再压入栈中 int ret = Integer.valueOf(str); stack.push(ret); } else { //字符串为运算符 int rightNum = stack.pop(); int leftNum = stack.pop(); switch (str) { case "+": stack.push(leftNum+rightNum); break; case "-": stack.push(leftNum-rightNum); break; case "*": stack.push(leftNum*rightNum); break; case "/": stack.push(leftNum/rightNum); break; } } } return stack.pop(); } private boolean isOperator(String str) { if(str.equals("+") || str.equals("-") || str.equals("*") || str.equals("/") ) { return true; } return false; } public static void main(String[] args) { evalRPN evalRPN = new evalRPN(); System.out.println(evalRPN.ergodic()); }}3.出栈入栈次序匹配
3.1问题描述
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
3.2思路分析
1.先去遍历第一个数组,每遍历到数组每一个元素先与压入栈中再看栈顶元素与另一个数组的第一个元素进行比较。
2.相同则弹出,并且第二个数组往后遍历反之第一个数组继续遍历并且压入栈中。
3.直到栈为空或者第一个数组遍历完。
3.3画图解释
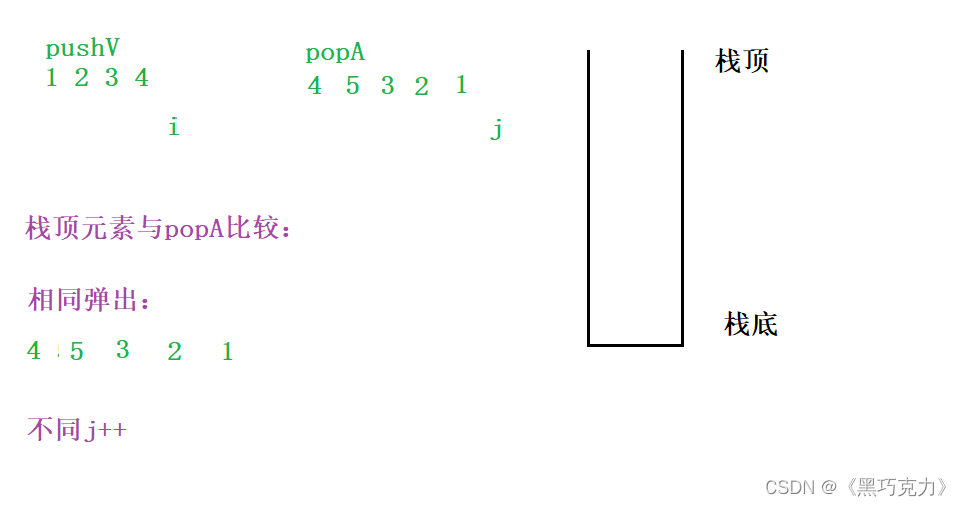
3.4代码实现
public class PushPopMatch { Stack<Integer> stack = new Stack<>(); public boolean IsPopOrder (int[] pushV, int[] popV) { int j =0; for (int i = 0; i < pushV.length; i++) { //1.压入栈中 stack.push(pushV[i]); //2.将栈顶元素与popV数组比较,相同则弹出并且j++,反之继续压栈。 //当这个条件stack.peek() == popV[j]出来了,你需要确保栈不能为空并且数组不能越界。 while(j<popV.length &&!stack.empty() && stack.peek() == popV[j]) { stack.pop(); j++; } } return stack.empty(); } public static void main(String[] args) { int[] pushA = {1,2,3,4,5}; int[] popA = {4,5,3,2,1}; PushPopMatch pushPopMatch = new PushPopMatch(); System.out.println(pushPopMatch.IsPopOrder(pushA, popA)); }}4.最小栈
4.1问题描述
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。
4.2思路分析
我们先想一想,一个栈可以完成这个目标吗?,明显的是不能满足时间复杂度,所以我们需要两个栈来解决这个问题,我们创建一个普通栈和一个最小栈。
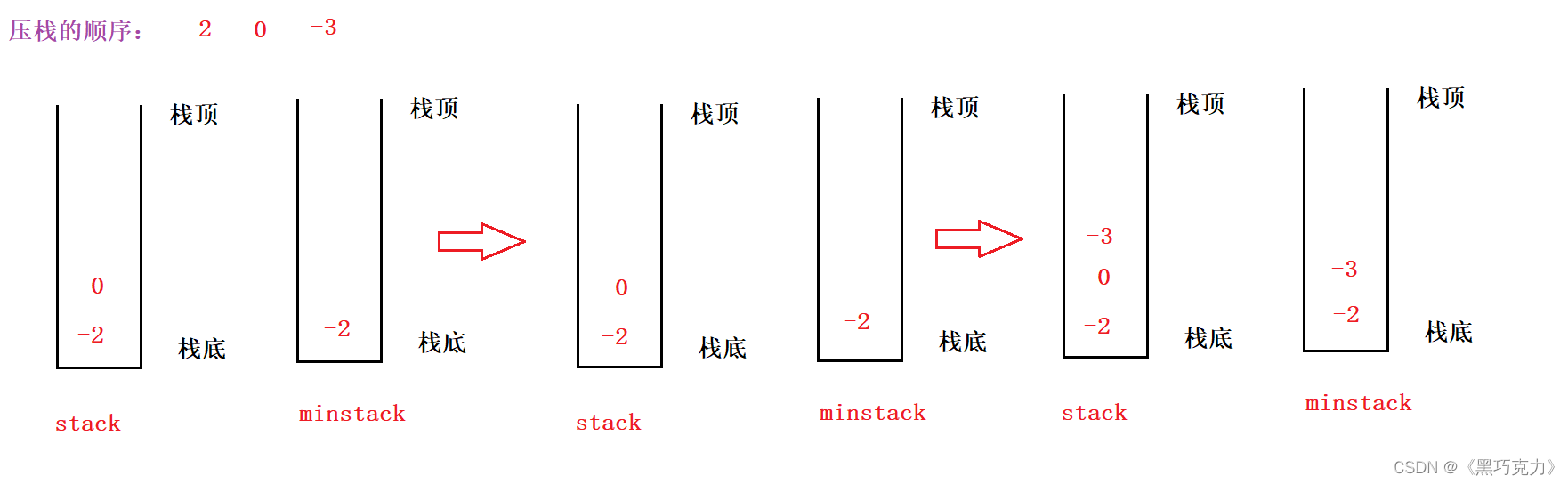
1.实现push操作:普通栈每一个元素都需要压栈,但最小栈有两种情况:
情况1:最小栈是空栈,那么第一个元素直接压入最小栈
情况2:最小栈不是空栈,则需要将压栈的元素与最小栈的栈顶元素进行比较,当满足压栈元素<=最小栈栈顶元素则压栈
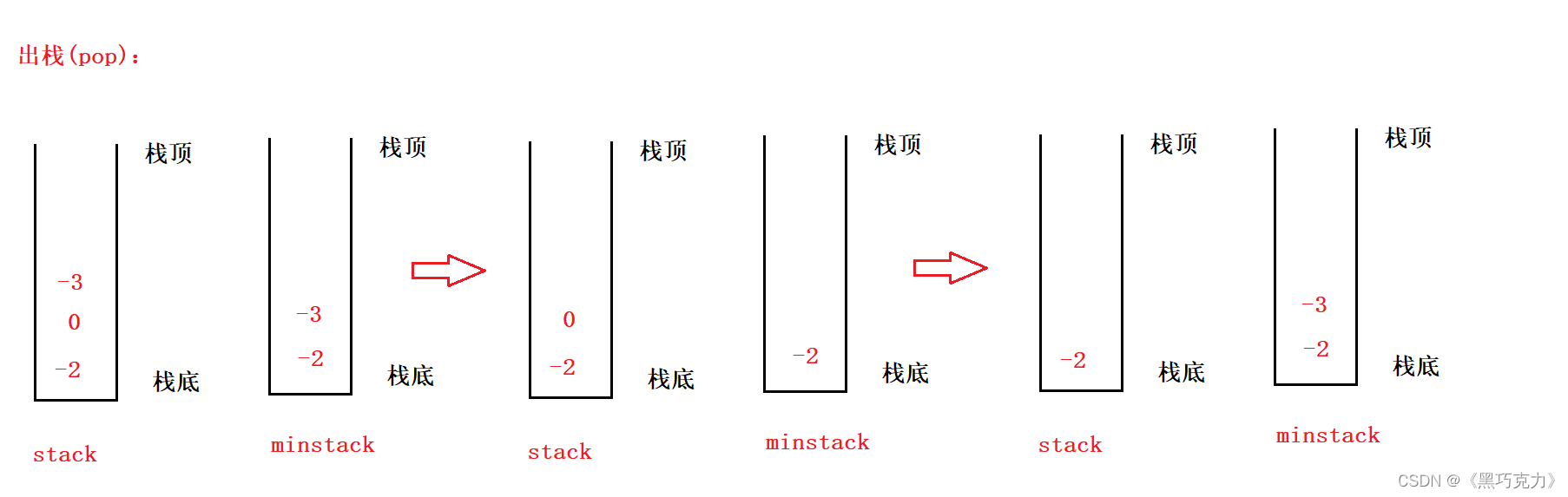
2. 实现pop操作:普通栈每一个元素都可以出栈,但最小栈有两种情况:
情况1:普通栈出栈的元素与最小栈的栈顶元素相同则都弹出
情况2:普通栈出栈的元素与最小栈的栈顶元素不相同,则普通栈弹出,最小栈不要弹出。
3.实现top操作:直接弹出普通栈的栈顶的元素。
4.实现getMin操作:直接弹出最小栈的栈顶元素
4.3画图分析
1.实现push操作:
2.实现pop操作:
4.4代码实现
public class GetMinStack { Stack<Integer> stack= new Stack<>(); Stack<Integer> Minstack= new Stack<>(); //push public void push(int val) { //普通栈直接压栈 stack.push(val); //最小栈压栈两种情况 if(Minstack.empty()) { //1.最小栈为空栈,直接压栈。 Minstack.push(val); } else { //2.最小栈不为空栈,则需要将压栈的元素与最小栈栈顶元素比较,当压栈元素<=最小栈栈顶元素则可以压栈 if(val <= Minstack.peek()) { Minstack.push(val); } } } //pop public void pop() { int ret = stack.pop(); if (ret == Minstack.peek()) { Minstack.pop(); } } //peek public int peek() { return stack.peek(); } //getMin public int getMin() { return Minstack.peek(); } public static void main(String[] args) { GetMinStack getMinStack = new GetMinStack(); getMinStack.push(-2); getMinStack.push(0); getMinStack.push(-3); System.out.println(getMinStack.getMin()); }}结尾:希望大家可以给我点点关注,点点赞,并且在评论区发表你们的想法和意见,我会认真看每一条评论,你们的支持就是我的最大鼓励。🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹🌹