1.原理
限制性立方样条(Restricted cubic spline,RCS)是分析非线性关系的最常见的方法之一。RCS用三次函数拟合不同节点之间的曲线并使其平滑连接,从而达到拟合整个曲线并检验其线性的过程。可以想见,RCS的节点数对拟合结果来说非常重要。通常,小于30个样本数的小样本取3个节点,大样本取5个节点。
2.R实现
1.cox回归
#Used for RCS(Restricted Cubic Spline)#我们使用rms包library(ggplot2)library(rms)library(survminer)library(survival)在这里我们使用survival包中的lung数据
#####基于cox回归#这里用survival包里的lung数据集来做范例分析head(lung)# inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss# 3 306 2 74 1 1 90 100 1175 NA# 3 455 2 68 1 0 90 90 1225 15# 3 1010 1 56 1 0 90 90 NA 15# 5 210 2 57 1 1 90 60 1150 11# 1 883 2 60 1 0 100 90 NA 0# 12 1022 1 74 1 1 50 80 513 0#status:censoring status 1=censored, 2=dead#sex:Male=1 Female=2#ph.ecog:医生对患者的体能状态评级#ph.karno:医生对患者的另一种体能状态评级karnofsky#pat.karno:患者karnofsky自评#meal.cal:摄入卡路里#wt.loss:过去半年体重减轻# 对数据进行打包,整理dd <- datadist(lung) #为后续程序设定数据环境options(datadist='dd') #为后续程序设定数据环境#用AIC法计算不同节点数选择下的模型拟合度来决定最佳节点数for (knot in 3:10) { fit <- cph(Surv(time,status) ~ rcs(meal.cal,knot) + sex+age , x=TRUE, y=TRUE,data=lung) tmp <- extractAIC(fit) if(knot==3){AIC=tmp[2];nk=3} if(tmp[2]<AIC){AIC=tmp[2];nk=knot}}nk #3#cox回归中自变量对HR的rcsfit <- cph(Surv(time,status) ~ rcs(meal.cal,3) + sex+age , x=TRUE, y=TRUE,data=lung)#大样本5节点,小样本(<30)3节点#比例风险PH假设检验,p>0.05满足假设检验cox.zph(fit,"rank")#非线性检验,p<0.05为有非线性关系anova(fit)#这里的结果是# Wald Statistics Response: Surv(time, status) ## Factor Chi-Square d.f. P # meal.cal 0.42 2 0.8113# Nonlinear 0.09 1 0.7643,呈线性# sex 6.61 1 0.0101# age 1.99 1 0.1582# TOTAL 10.29 4 0.0358#查看各meal.cal对应的HR值HR<-Predict(fit, meal.cal,fun=exp)head(HR)#画图ggplot()+ geom_line(data=HR, aes(meal.cal,yhat), linetype="solid",size=1,alpha = 0.7,colour="#0070b9")+ geom_ribbon(data=HR, aes(meal.cal,ymin = lower, ymax = upper), alpha = 0.1,fill="#0070b9")+ theme_classic()+ geom_hline(yintercept=1, linetype=2,size=1)+ labs(title = "Lung Cancer Risk", x="Age", y="HR (95%CI)") 画出来的结果如图:
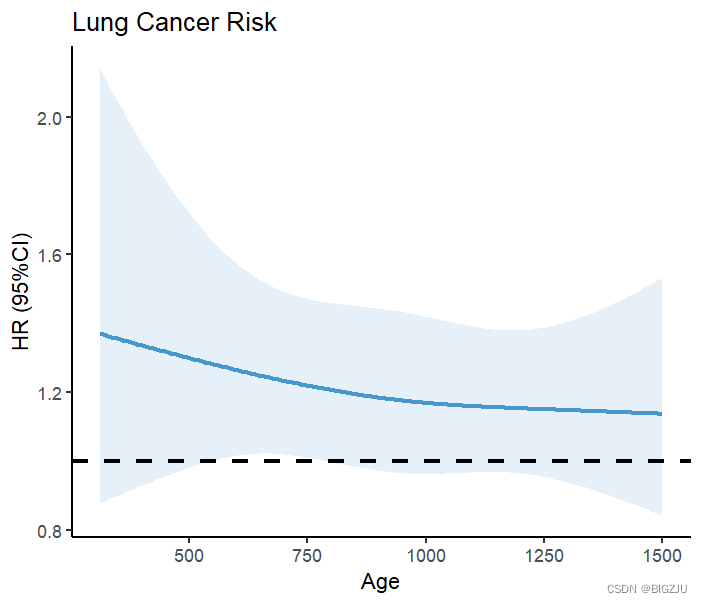
anova(fit)的结果以及可视化呈现显示在RCS下饮食能量摄入和死亡率之间的关系呈线性。
我们再找一个非线性的例子,这个例子使用survival包的colon数据:
#结肠癌病人数据Colon <- colonColon$sex <- as.factor(Colon$sex)#1 for male,0 for femaleColon$etype <- as.factor(Colon$etype-1)dd <- datadist(Colon)options(datadist='dd') for (knot in 3:10) { fit <- cph(Surv(time,etype==1) ~ rcs(age,knot) +sex , x=TRUE, y=TRUE,data=Colon) tmp <- extractAIC(fit) if(knot==3){AIC=tmp[2];nk1=3} if(tmp[2]<AIC){AIC=tmp[2];nk1=knot}}nk1 #3fit <- cph(Surv(time,etype==1) ~ rcs(age,3) +sex , x=TRUE, y=TRUE,data=Colon)cox.zph(fit,"rank")anova(fit)# Wald Statistics Response: Surv(time, etype == 1) ## Factor Chi-Square d.f. P # age 6.90 2 0.0317# Nonlinear 6.32 1 0.0120,非线性# sex 1.20 1 0.2732# TOTAL 7.54 3 0.0565HR<-Predict(fit, age,fun=exp)head(HR)ggplot()+ geom_line(data=HR, aes(age,yhat), linetype="solid",size=1,alpha = 0.7,colour="#0070b9")+ geom_ribbon(data=HR, aes(age,ymin = lower, ymax = upper), alpha = 0.1,fill="#0070b9")+ theme_classic()+ geom_hline(yintercept=1, linetype=2,size=1)+ geom_vline(xintercept=47.35176,size=1,color = '#d40e8c')+#查表HR=1对应的age geom_vline(xintercept=65.26131,size=1,color = '#d40e8c')+ labs(title = "Colon Cancer Risk", x="Age", y="HR (95%CI)") 结果如下: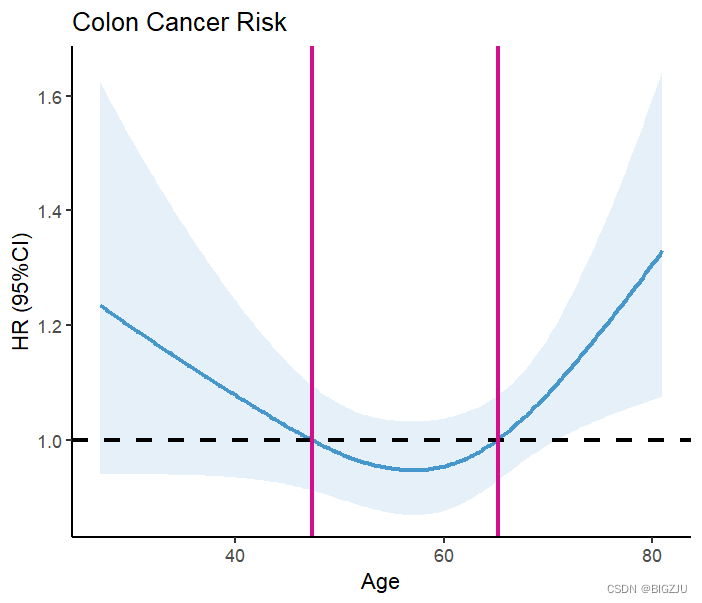
anova(fit)的结果以及可视化呈现显示该示例呈现非线性关系
我们还可以进行分组的研究和可视化呈现,只需修改Predict()函数中的参数
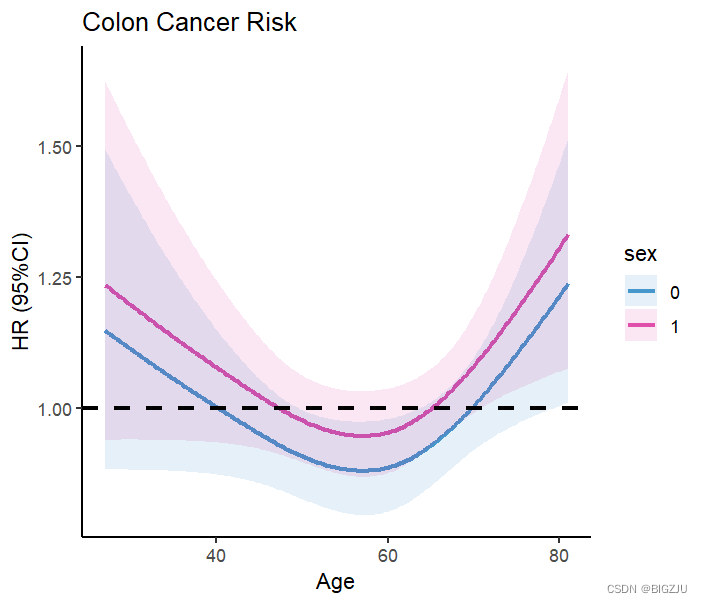
HR1 <- Predict(fit, age, sex=c('0','1'), fun=exp,type="predictions", conf.int = 0.95,digits =2)HR1ggplot()+ geom_line(data=HR1, aes(age,yhat, color = sex), linetype="solid",size=1,alpha = 0.7)+ geom_ribbon(data=HR1, aes(age,ymin = lower, ymax = upper,fill = sex), alpha = 0.1)+ scale_color_manual(values = c('#0070b9','#d40e8c'))+ scale_fill_manual(values = c('#0070b9','#d40e8c'))+ theme_classic()+ geom_hline(yintercept=1, linetype=2,size=1)+ labs(title = "Colon Cancer Risk", x="Age", y="HR (95%CI)")
结果:
2.logistic回归
如果不是cox回归,用的是logistic回归,总体差不多,只需要替代模型就行
#####基于logistic回归的rcs#建模型fit <-lrm(status ~ rcs(age, 3)+sex,data=lung) OR <- Predict(fit, age,fun=exp)#画图ggplot()+ geom_line(data=OR, aes(age,yhat), linetype="solid",size=1,alpha = 0.7,colour="#0070b9")+ geom_ribbon(data=OR, aes(age,ymin = lower, ymax = upper), alpha = 0.1,fill="#0070b9")+ theme_classic()+ geom_hline(yintercept=1, linetype=2,size=1)+ geom_vline(xintercept=38.93970,size=1,color = '#d40e8c')+ #查表OR=1对应的age labs(title = "Lung Cancer Risk", x="Age", y="OR (95%CI)")3.线性回归
线性回归也一样
#####基于线性回归的rcsfit <- ols(meal.cal ~rcs(age,3)+sex,data=lung)Kcal <- Predict(fit,age)#画图ggplot()+ geom_line(data=Kcal, aes(age,yhat), linetype="solid",size=1,alpha = 0.7,colour="#0070b9")+ geom_ribbon(data=Kcal, aes(age,ymin = lower, ymax = upper), alpha = 0.1,fill="#0070b9")+ theme_classic()+ labs(title = "RCS", x="Age", y="Kcal")