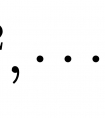K-Means聚类算法及其python实现（已附上代码至本博客）

点击全文阅读

目录

一、算法公式讲解二、算法流程三、算法实现代码四、代码结果分析五、K-Means库函数六、K-Means算法时间复杂度
觉得有用的,一腚要先点赞后收藏!!!气死人了,40多个收藏0点赞!!

一、算法公式讲解

对于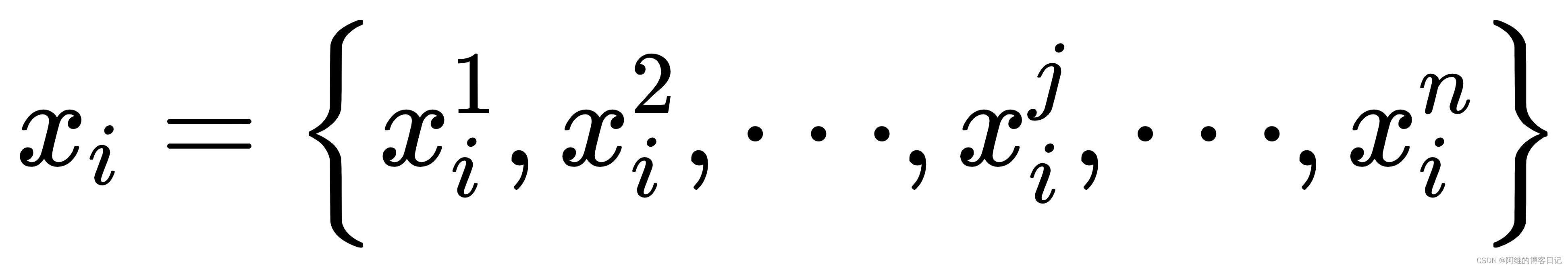
n代表了x有n维，x上标j表示第j维的特征，下标i表示该向量是第i个样本

簇中心坐标为：（当然，这也是重新计算簇中心坐标的方法！！）
向量 u i = ( u i ( 1 ) , u i ( 2 ) , ⋅ ⋅ ⋅ , u i ( j ) , ⋅ ⋅ ⋅ , u i ( n ) ) u_i=(u_i^{(1)} ,u_i^{(2)}, ···, u_i^{(j)},···,u_i^{(n)}) ui​=(ui(1)​,ui(2)​,⋅⋅⋅,ui(j)​,⋅⋅⋅,ui(n)​)，然后标量

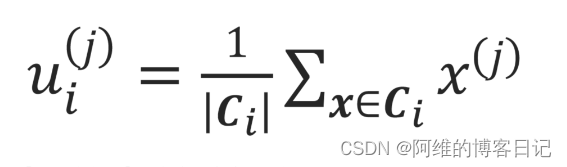
其中一个维度,这里比如说是第2个样本的第1维特征 u 2 1 u_{2}^{1} u21​,我就到这个第二个簇里面把这个簇所有点第一特征求和得到sum，然后把总和sum除以这个簇的大小| C 2 C_2{} C2​|(这个簇里面点的个数)，然后就得到第2簇的簇中心的第1维的特征（坐标）
比如第一簇的簇中心坐标：

u 1 = ( u 1 ( 1 ) , u 1 ( 2 ) , u 1 ( 3 ) ) u_1=(u_1^{(1)} ,u_1^{(2)},u_1^{(3)}) u1​=(u1(1)​,u1(2)​,u1(3)​)
属于第一簇的坐标有
x 2 = ( 1 , 2 , 3 ) x_2=(1 ,2,3) x2​=(1,2,3)
x 3 = ( 4 , 5 , 6 ) x_3=(4 ,5,6) x3​=(4,5,6)
x 4 = ( 7 , 8 , 9 ) x_4=(7 ,8,9) x4​=(7,8,9)

则

u 1 = ( 1 + 4 + 7 3 , 2 + 5 + 8 3 , 3 + 6 + 9 3 ) = ( 4 , 5 , 6 ) u_1=(\frac{1+4+7}{3} ,\frac{2+5+8}{3},\frac{3+6+9}{3} )=(4,5,6) u1​=(31+4+7​,32+5+8​,33+6+9​)=(4,5,6)

二、算法流程

K-means算法首先随机分布簇中心，然后计算簇中心并重新分簇为一个周期进行迭代，直到簇稳定为止，

三、算法实现代码

有Kmeans.py和kmeansSamples.txt两个文件，kmeansSamples.txt记录的是所有点的坐标，Kmeans.py描述算法实现
Kmeans.py文件如下

# -*- coding: utf-8 -*-import numpy as npimport matplotlib.pyplot as pltdef L2(vecXi, vecXj):    '''    计算欧氏距离    para vecXi：点坐标，向量    para vecXj：点坐标，向量    retrurn: 两点之间的欧氏距离    '''    return np.sqrt(np.sum(np.power(vecXi - vecXj, 2)))def kMeans(S, k, distMeas=L2):    '''    K均值聚类    para S：样本集，多维数组    para k：簇个数    para distMeas：距离度量函数，默认为欧氏距离计算函数    return sampleTag：一维数组，存储样本对应的簇标记    return clusterCents：一维数组，各簇中心    retrun SSE:误差平方和    '''    print('k = ' , k)    m = np.shape(S)[0] # 样本总数    sampleTag = np.zeros(m)    print('sampleTag.shape=',sampleTag)    # 随机产生k个初始簇中心    n = np.shape(S)[1] # 样本向量的特征数    print('n = ' , n)    clusterCents = np.mat([[-1.93964824,2.33260803],[7.79822795,6.72621783],[10.64183154,0.20088133]])    #clusterCents = np.mat(np.zeros((k,n)))    #for j in range(n):    #    minJ = min(S[:,j])     #    rangeJ = float(max(S[:,j]) - minJ)    #    clusterCents[:,j] = np.mat(minJ + rangeJ * np.random.rand(k,1))            sampleTagChanged = True    SSE = 0.0    while sampleTagChanged: # 如果没有点发生分配结果改变，则结束        sampleTagChanged = False        SSE = 0.0                # 计算每个样本点到各簇中心的距离        # m是样本总数        for i in range(m):            minD = np.inf            minIndex = -1            # k是簇中心个数            for j in range(k):                # S样本集，clusterCents样本中心点                d = distMeas(clusterCents[j,:],S[i,:])                if d < minD:                    minD = d                    minIndex = j            if sampleTag[i] != minIndex:                 sampleTagChanged = True            sampleTag[i] = minIndex            SSE += minD**2        print(clusterCents)        plt.scatter(clusterCents[:,0].tolist(),clusterCents[:,1].tolist(),c='r',marker='^',linewidths=7)        plt.scatter(S[:,0],S[:,1],c=sampleTag,linewidths=np.power(sampleTag+0.5, 2))        plt.show()        print(SSE)                # 重新计算簇中心        for i in range(k):            ClustI = S[np.nonzero(sampleTag[:]==i)[0]]            clusterCents[i,:] = np.mean(ClustI, axis=0)    return clusterCents, sampleTag, SSEif __name__=='__main__':    samples = np.loadtxt("kmeansSamples.txt")    clusterCents, sampleTag, SSE = kMeans(samples, 3)    #plt.scatter(clusterCents[:,0].tolist(),clusterCents[:,1].tolist(),c='r',marker='^')    #plt.scatter(samples[:,0],samples[:,1],c=sampleTag,linewidths=np.power(sampleTag+0.5, 2))    plt.show()    print(clusterCents)    print(SSE)

kmeansSamples.txt文件如下

8.764743691132109049e+00 1.497536962729086341e+014.545778445909218313e+00 7.394332431706460262e+005.661841772908352333e+00 1.045327224311696668e+016.020055532521467967e+00 1.860759073162559929e+011.256729723000295529e+01 5.506569916803323750e+004.186942275051188211e+00 1.402615035721461290e+015.726706075832996845e+00 8.375613974148174989e+004.099899279500291094e+00 1.444273323355928795e+012.257178930021525254e+00 1.977895587652345855e+004.669135451288612515e+00 7.717803834787531070e-018.121947597697801058e+00 7.976212807755792555e-017.972277764807800260e-02 -1.938666197338206221e+008.370047062442882435e+00 1.077781799178707622e+016.680973199869320922e+00 1.553118858170866545e+015.991946943553537963e+00 1.657732863976965021e+015.641990155271871643e+00 1.554671013661827672e+01-2.925147643580102041e+00 1.108844569740028163e+014.996949605297930752e+00 1.986732057663068707e+003.866584099986317025e+00 -1.752825909916766900e+002.626427441224858939e+00 2.208897582166075324e+015.656225833870900388e+00 1.477736974879376675e+01-3.388227926726261607e-01 5.569311423852095544e+001.093574481611491223e+01 1.124487205516641275e+014.650235760178413003e+00 1.278869502885029341e+018.498485127403823114e+00 9.787697108749913610e+007.530467091751554598e+00 8.502325665434069535e+006.171183705302398792e+00 2.174394049079376856e+01-9.333949569013078040e-01 1.594142490265068712e+00-6.377004909329702542e+00 3.463894089865578341e+007.135980906743346175e+00 1.417794597480970609e+01

四、代码结果分析

第一次迭代，簇中心分布不太合理（红色三角形代表簇中心）

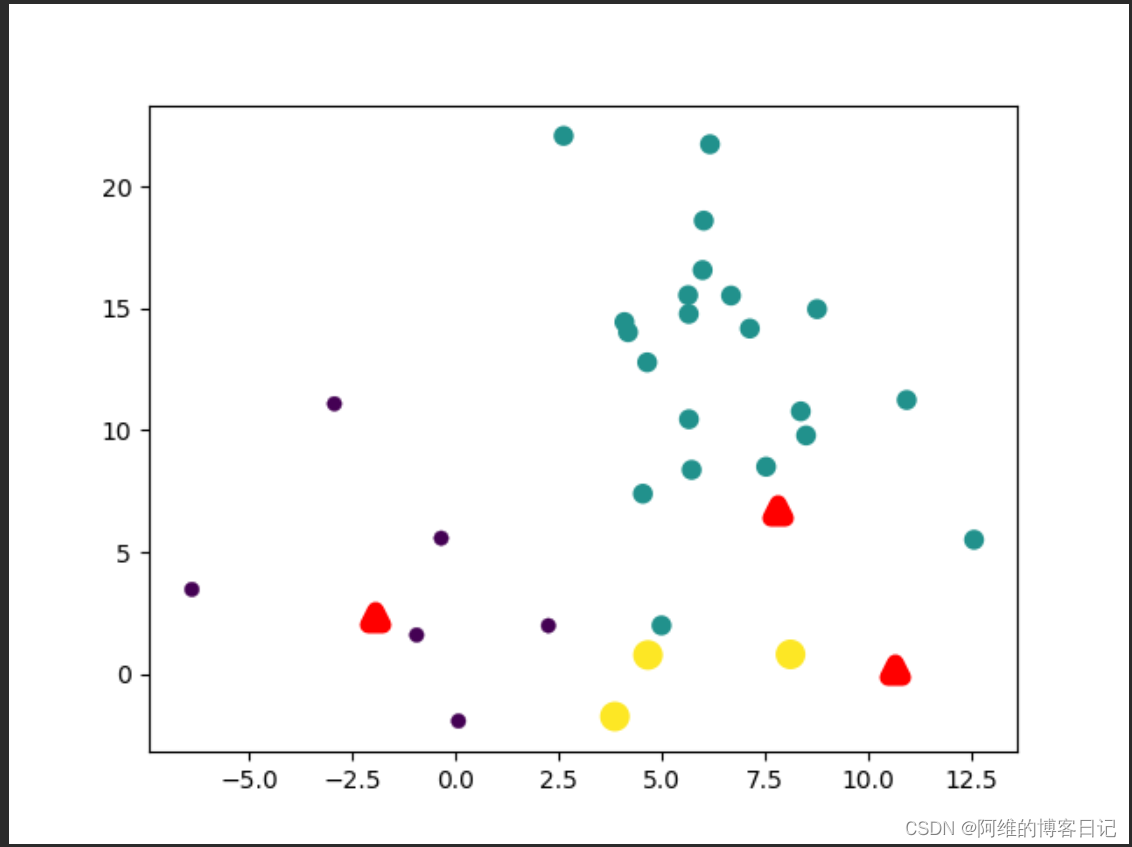
第二次迭代，簇中心重新计算，因此簇中心分布比第一次更合理

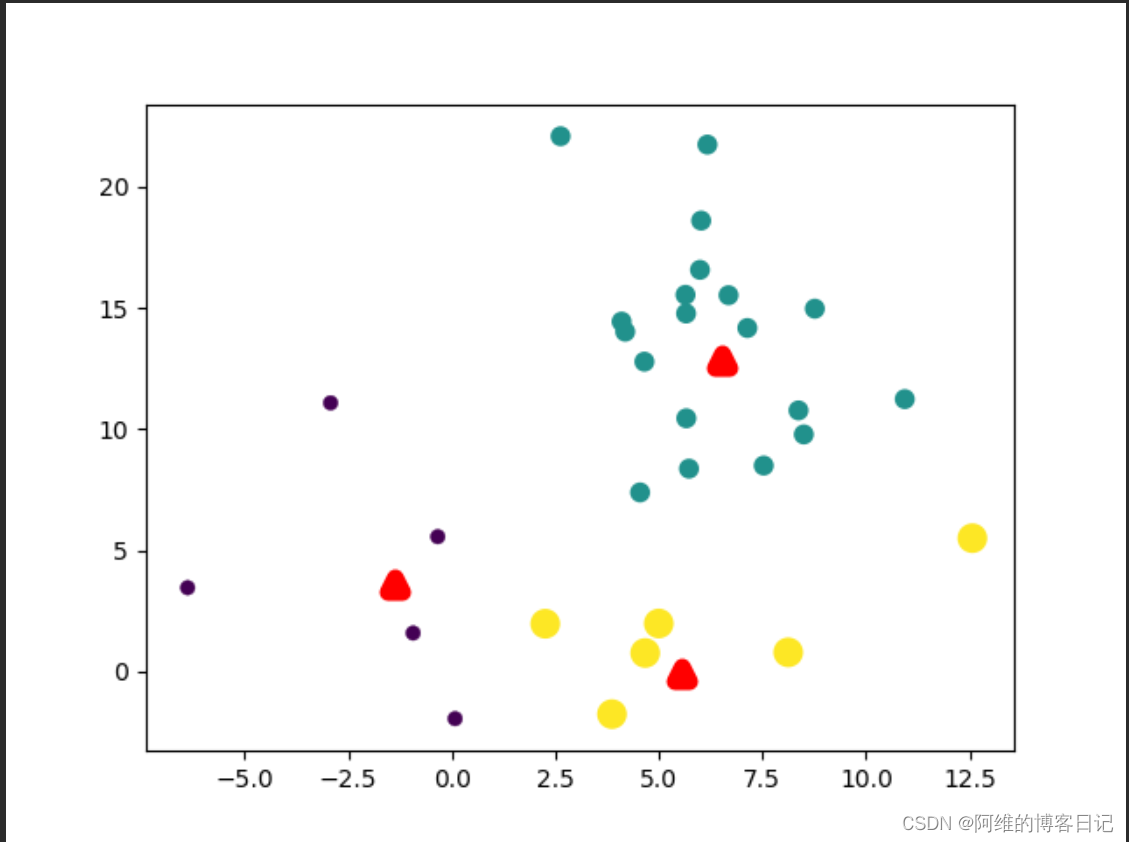
第3次迭代

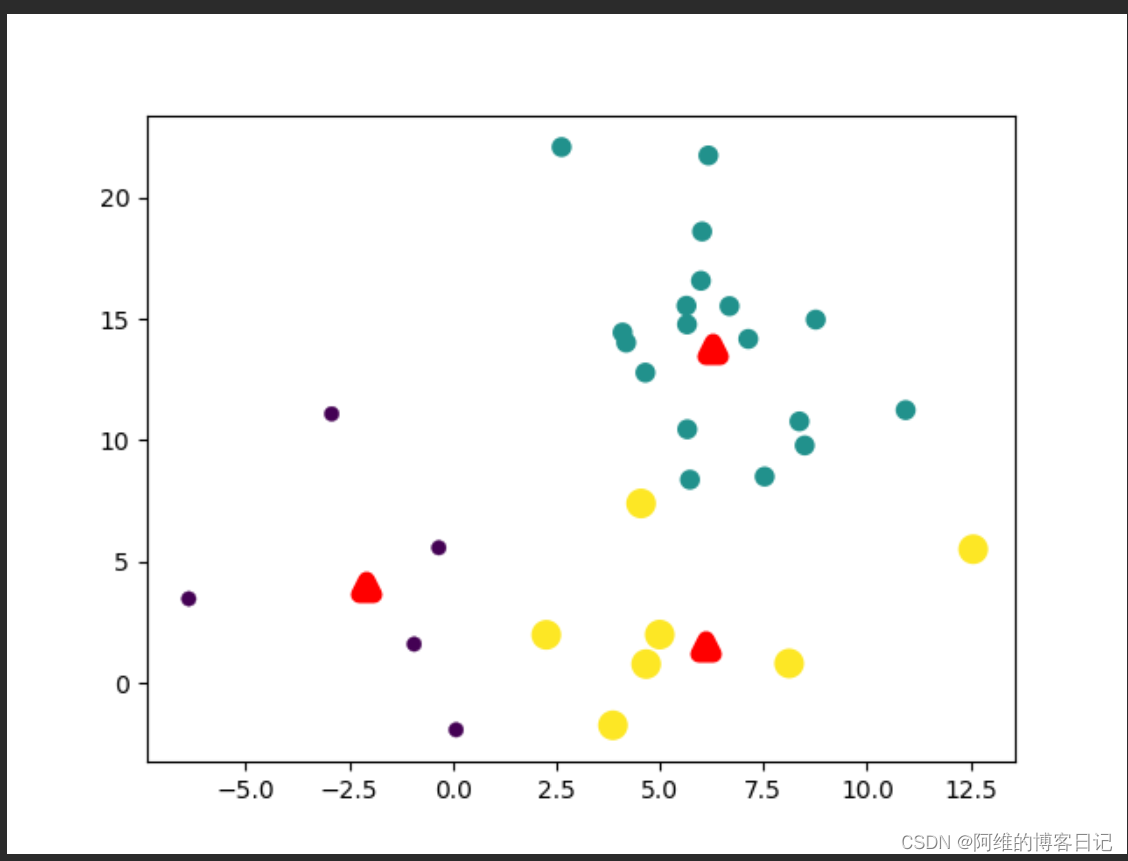
第四次迭代

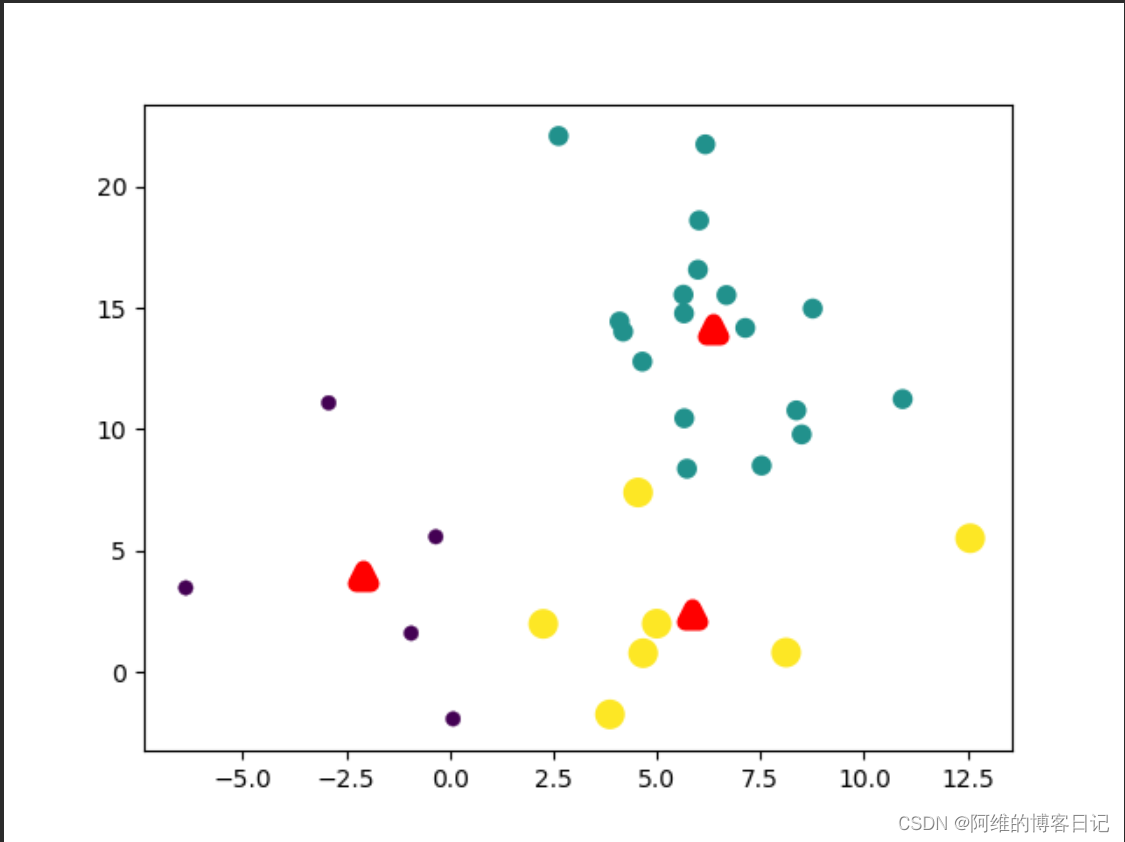
五、K-Means库函数

KMeans(n_clusters=8, *, init=‘k-means++’, n_init=‘k-means++’, n_init=10,max_iter=300, tol=0.0001, verbose=0, random_state=None, copy_x=True, algorithm=‘auto’)
链接🔗：👉Sklearn关于K-Means的API介绍
相关输人参数和返回值，在网站上有详细介绍，建议 直接看原版文档，这里仅介绍几个重要参数，其他内容不再赘述。

init 参数提供了三种产生筷中心的方法：“K-means++”指定产生较大间距的筷中心(2.1.4节)；“random”指定随机产生簇中心；由用户通过一个ndarrav 数组指定初始筷中心。n_init 参数指定了算法运行次数，它在不指定初始筷中心时，通过多次运行算法，最终选择最好的结果作为输出。 max iter 参数指定了一次运行中的最大迭代次数。在大规模数据集中，算法往往要耗费大量的时间，可通过指定迭代次数来折中耗时和效果。tol 参数指定了算法收敛的國值。在大规模数据集中，算法往往难以完全收敛，即达到连续两次相同的分筷需要耗费很长时间,可通过指定國值来折中耗时和最优目标。algorithm 参数指定了是否采用elkan k-means 算法来简化距离计算。该算法比经典的k-means 算法在迭代速度方面有很大的提高。但该算法不适用于稀疏的样本数据。值“full”指定采用经典k-means 算法。值“ellkan”指定采用 elkan k-means 算法。值“auto”自动选择，在稠密数据时采用 elkan k-means 算法，在稀疏数据时采用经典k-means 算法。

六、K-Means算法时间复杂度

设样本总数为 m，分簇数为k。一次迭代过程中，以样本与簇中心的距离计算为基本运算,需要 m × k m \times k m×k。如果迭代次数为t（，则算法的时间复杂度是 O( m × k × t m \times k \times t m×k×t)。
算法运行不需要增长额外辅助空问，以样本和簇中心存储空间为基本空间,空间复杂度是0（ m + k m+k m+k）。
由于m,k,t可认为是常量,因此算法的时间复杂度和空间复杂度都可认为是线性的 O ( N ) O(N) O(N) .

点击全文阅读