1. ARIMA模型介绍
ARIMA模型是时间序列分析中的一种常用方法,主要用于理解和预测未来的时间序列数据。ARIMA是Autoregressive Integrated Moving Average的缩写,通常被翻译为自回归积分移动平均模型。ARIMA模型结合了以下三种主要部分:
AR(自回归)模型:在一个AR模型中,当前时间序列的值是前一期或多期值的函数。例如,一个AR(1)模型可以表示为:X(t) = c + φ*X(t-1) + e(t),其中X(t-1)是前一期的值,φ是模型参数,c是常数项,e(t)是误差项。
I(积分):这是ARIMA模型与ARMA模型的主要区别。积分部分涉及到对时间序列进行一次或多次差分,以达到使时间序列平稳的目的。平稳性是AR和MA模型的一个重要假设。
MA(移动平均)模型:在一个MA模型中,当前时间序列的值是过去误差项的函数。例如,一个MA(1)模型可以表示为:X(t) = μ + e(t) + θ*e(t-1),其中e(t-1)是前一期的误差项,θ是模型参数,μ是序列平均值,e(t)是当前的误差项。
ARIMA模型通常表示为ARIMA(p,d,q),其中p是AR部分的阶数,d是差分次数,q是MA部分的阶数。例如,ARIMA(1,1,1)模型表示一阶自回归、一阶差分和一阶移动平均都被包含在模型中。
ARIMA模型在经济学、金融学、工程学等许多领域都有广泛的应用,尤其是在预测经济或金融时间序列数据方面。
2.MATLAB代码
clear all;clc;close all;
% 在这个示例中,arima(p,d,q)创建一个ARIMA模型。在ARIMA模型中,d代表差分阶数,用于使非平稳序列变为平稳序列。estimate(Mdl,data)函数用于估计模型参数。infer(EstMdl,data)函数生成模型的预测。
% 请注意,你需要根据你的数据和特定需求来选择合适的模型阶数,并可能需要对此代码进行一些修改。
% 导入或创建数据
% 例如,我们生成一个1000个元素的随机序列
data = randn(1000,1);
% 定义ARIMA模型阶数
p = 1; % AR阶数
d = 1; % 差分阶数
q = 1; % MA阶数
% 创建ARIMA模型
Mdl = arima(p,d,q);
% 估计ARIMA模型参数
EstMdl = estimate(Mdl,data);
disp('ARIMA模型');
EstMdl
% 生成预测
[Y, E] = infer(EstMdl,data);
% 绘制结果
figure
subplot(2,1,1)
plot(data)
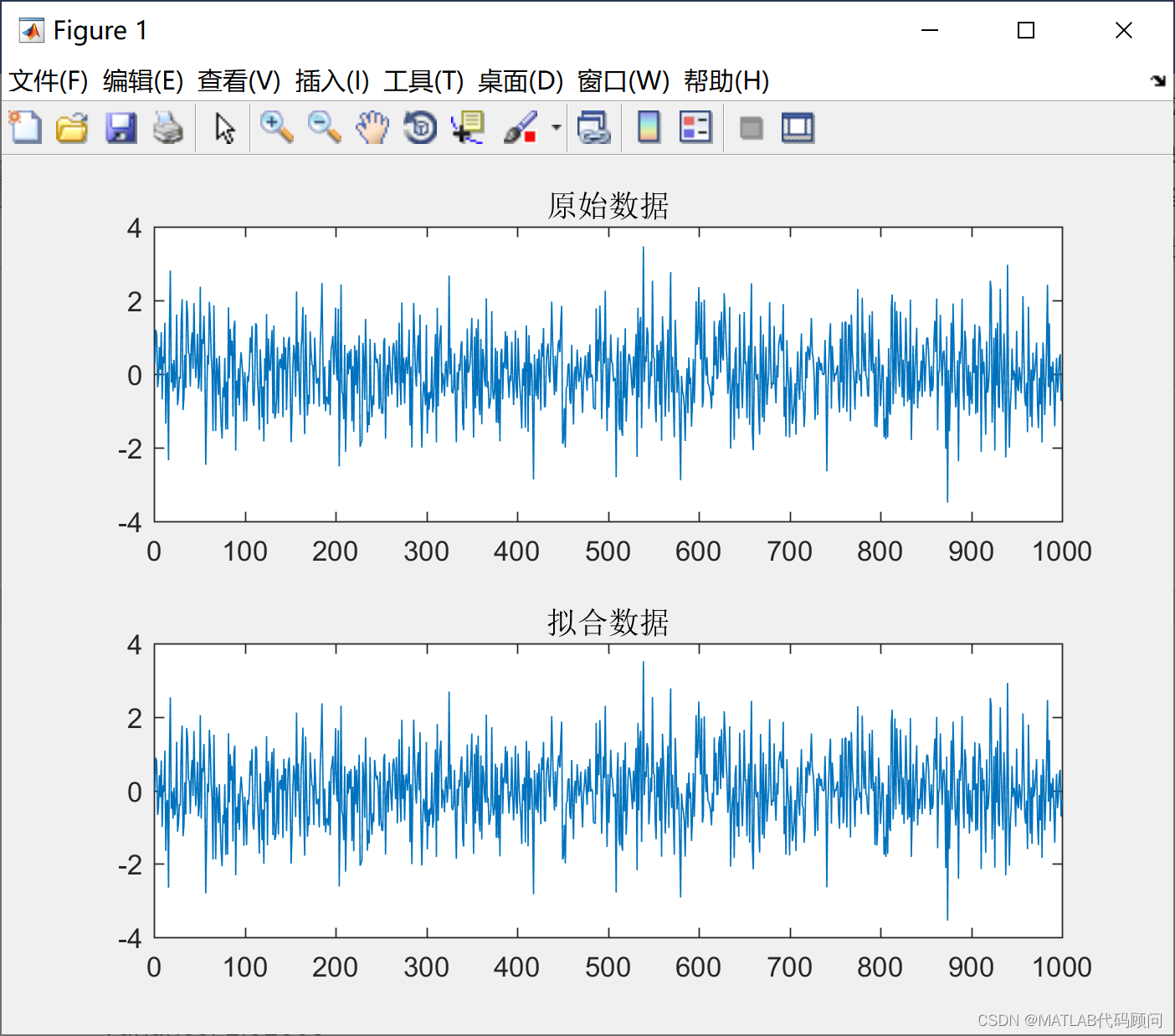
title('原始数据')
subplot(2,1,2)
plot(Y)
title('拟合数据')
3.程序结果
ARIMA(1,1,1) Model:
--------------------
Conditional Probability Distribution: Gaussian
Standard t
Parameter Value Error Statistic
----------- ----------- ------------ -----------
Constant -0.000254993 0.000271175 -0.940326
AR{1} -0.0164647 0.0324355 -0.507614
MA{1} -0.992399 0.00409856 -242.134
Variance 1.01605 0.0443788 22.8949
ARIMA模型
EstMdl =
ARIMA(1,1,1) Model:
--------------------
Distribution: Name = 'Gaussian'
P: 2
D: 1
Q: 1
Constant: -0.000254993
AR: {-0.0164647} at Lags [1]
SAR: {}
MA: {-0.992399} at Lags [1]
SMA: {}
Variance: 1.01605
>>