1. LCR 008. 长度最小的子数组
题目
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
题目链接
. - 力扣(LeetCode)
画图 和 文字 分析
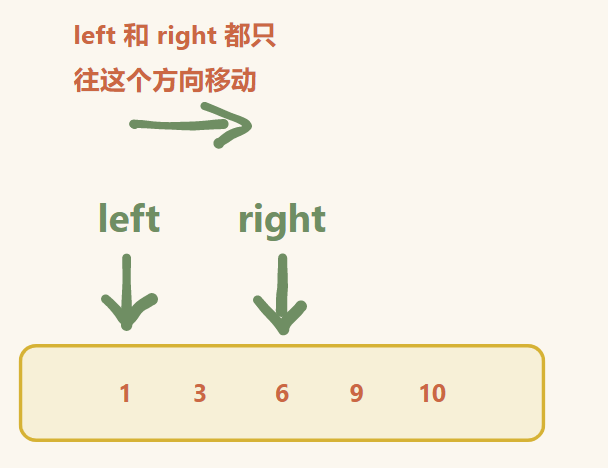
先说说有关滑动窗口的知识
滑动窗口特征和步骤:
无论是出窗口,还是进窗口,都是往一个方向上移动(不会后退)步骤: 进窗口检查出窗口更新数据(具体放的位置因题而异)
回到这道题,为什么符合滑动窗口的思想呢?
让 left = 0 , right = 0
通过 right 遍历数组 ,得到区间的所有数之和 sum
sum 与 target 相比
如果 sum < targetright++(进窗口)
2. 如果 sum >= target (检查)
记录此时的区间长度 (更新数据)
left++(出窗口), sum -= (left 之前所指向的数),直到 回到第一种情况(里层循环结束条件)
外层循环结束条件(right >= n)
注意:
记录我们用 count 表示,由于求最小长度,count 的初始化为 INT_MAX , 如果最后没有进入更新数据那一块(整个数组之和 < target),记得判断 count 的值
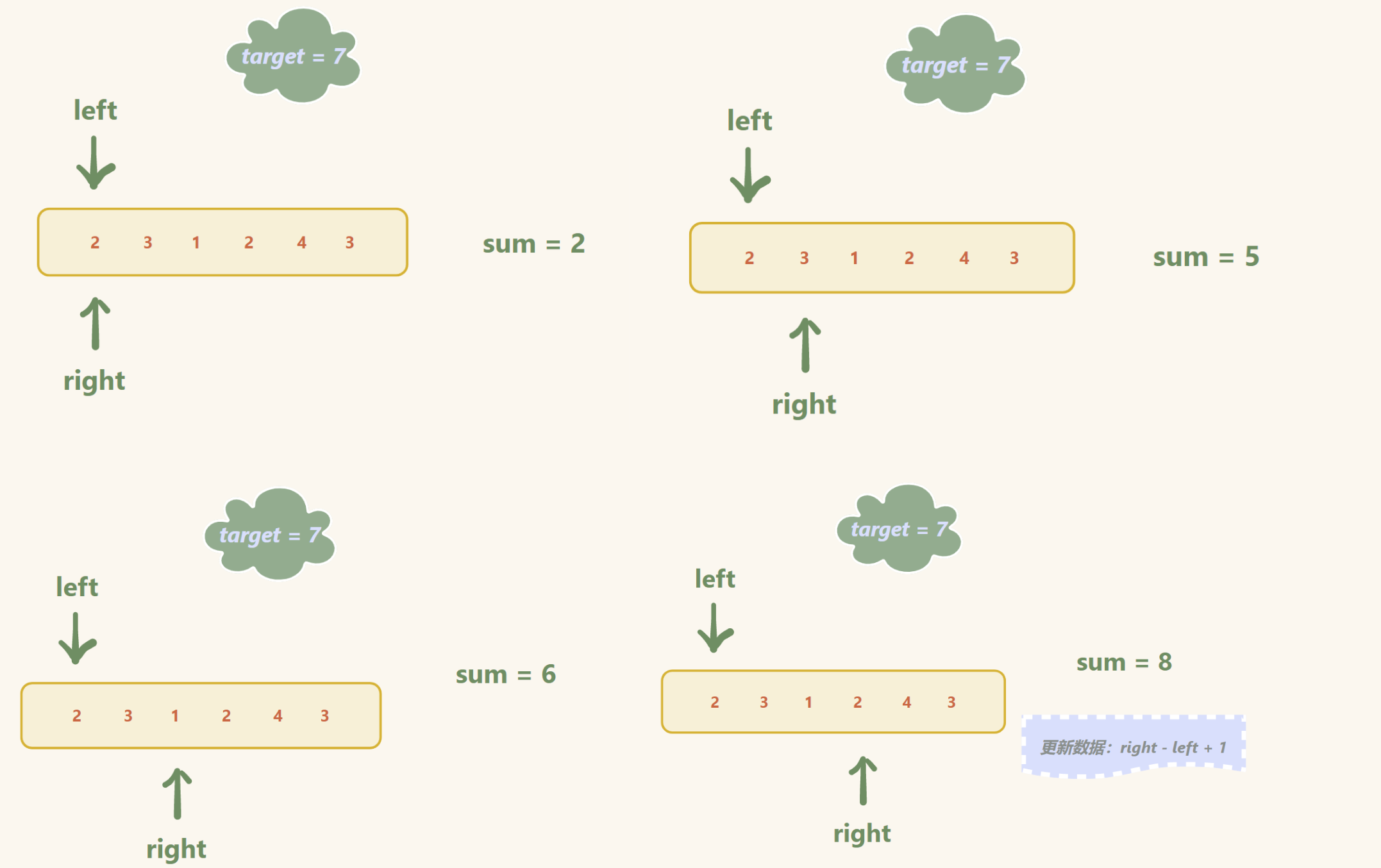
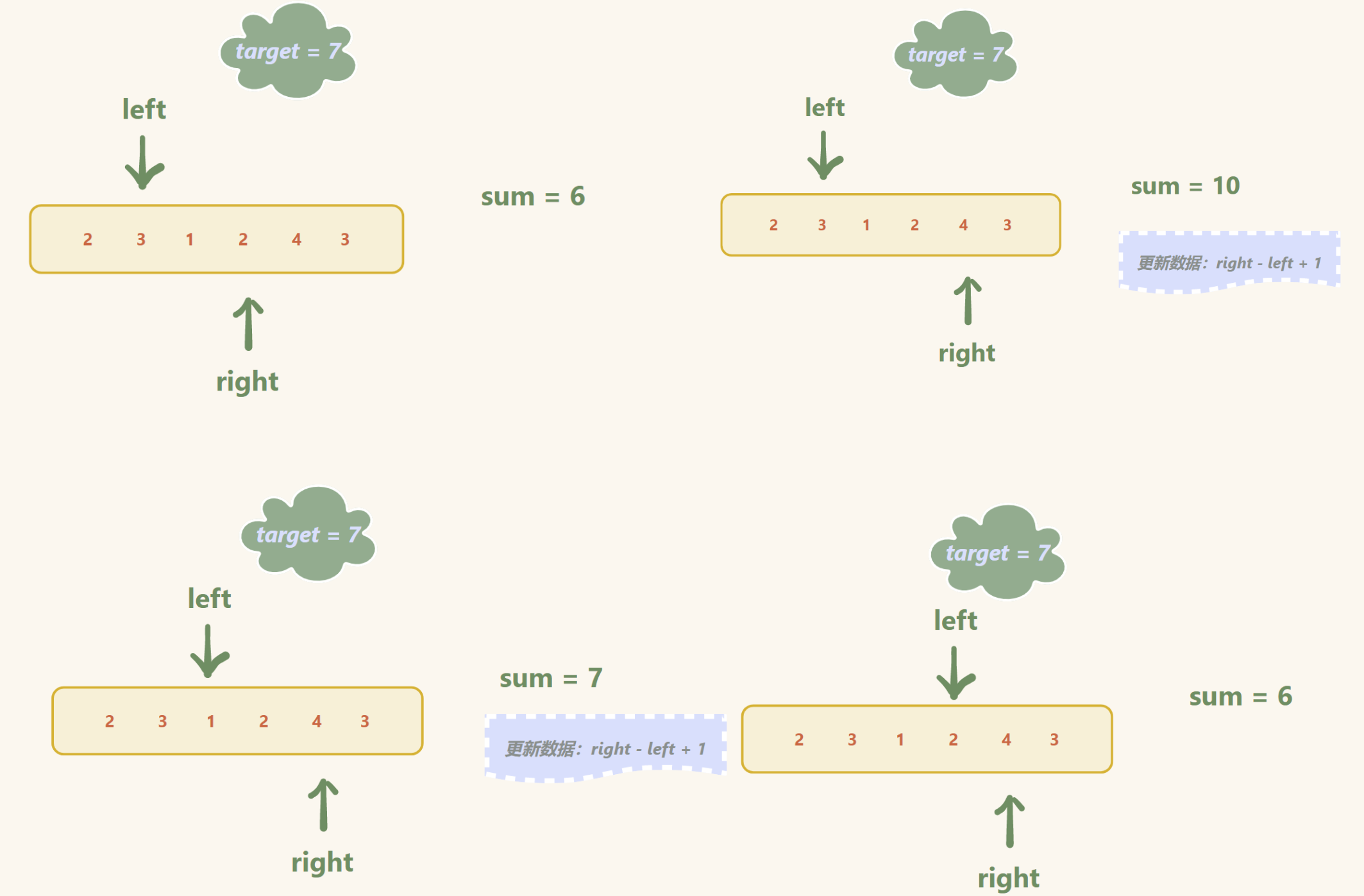
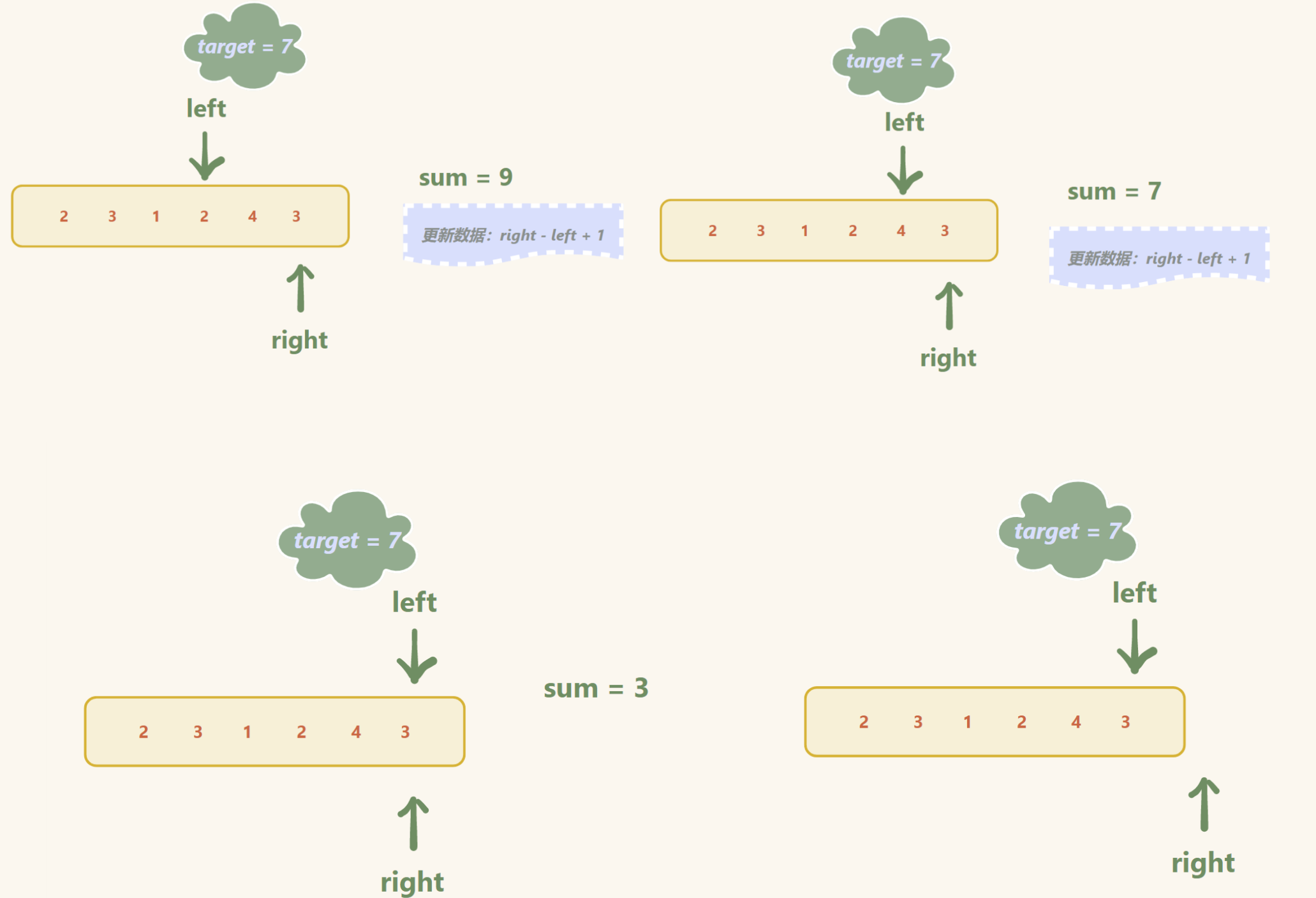
举例:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
代码
class Solution {public: int minSubArrayLen(int target, vector<int>& nums) { int sum =0; int left = 0; int right = 0; int count = INT_MAX; while(right < nums.size()) { sum += nums[right]; while(sum >= target) { if(right - left + 1 < count) { count = right - left + 1; } left++; sum -= nums[left - 1]; } right++; } if(count == INT_MAX) { count = 0; } return count; }};
2. LCR 016. 无重复字符的最长子串
题目
给定一个字符串 s ,请你找出其中不含有重复字符的 最长连续子字符串 的长度。
题目链接
. - 力扣(LeetCode)
画图 和 文字 分析
步骤:
定义两个指针 , left = 0 , right = 0 , hash数组(存放字符的个数)
当 hash[right] <= 1right++(进窗口)
2. 当 hash[right] > 1(出窗口)
更新数据
left++ ,同时 hash[left - 1]-- ,直到回到第一种情况(里层循环结束条件)
外层结束条件(right >= n)
注意:
这种方法存在遗漏的情况,跳出整个循环后,一定要最后更新一下(如果碰到整个数组都没有重复元素的情况,不最后检查一下就是错误的)如果不想实现注意事项一,那么把更新数据提前到进窗口那一步即可
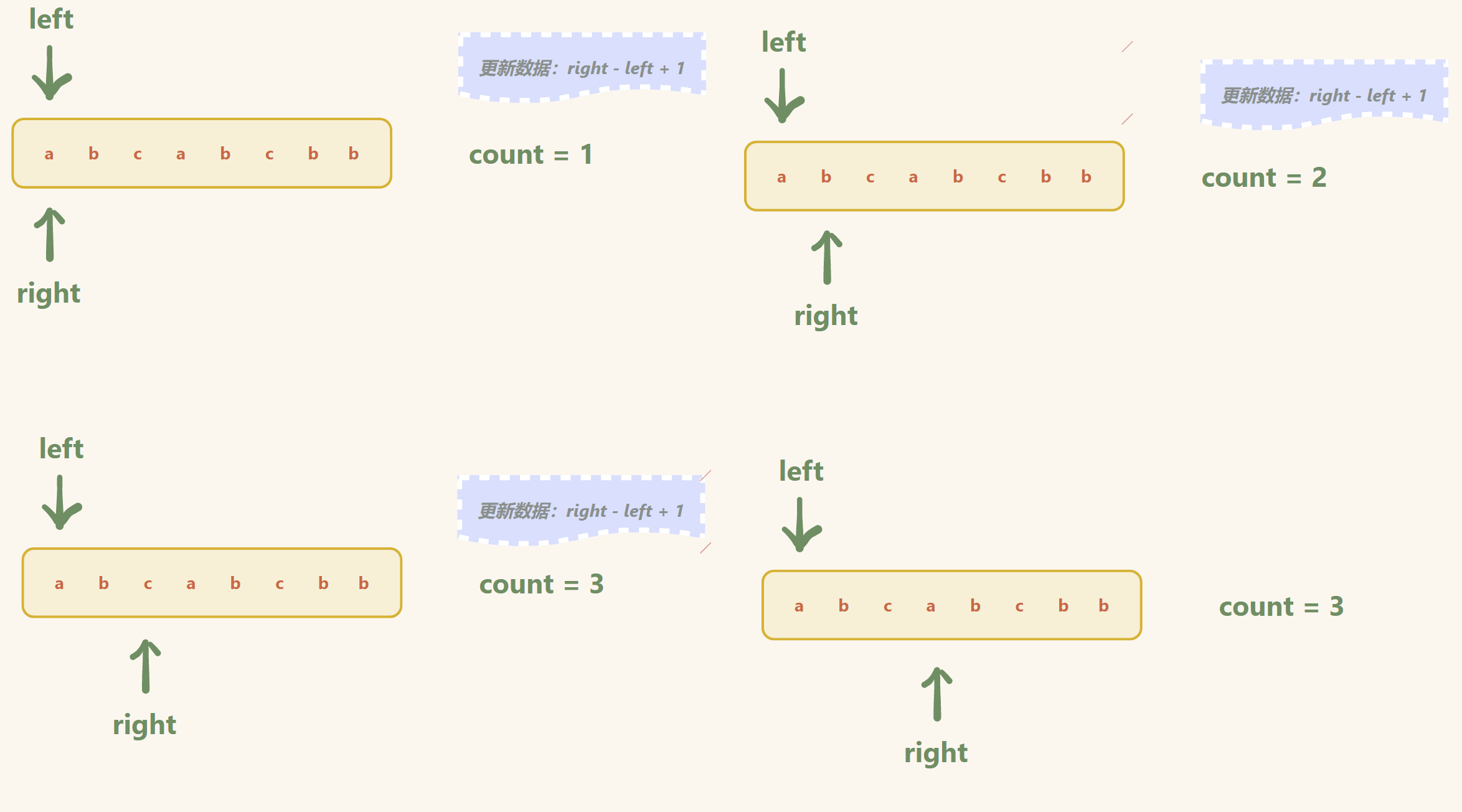
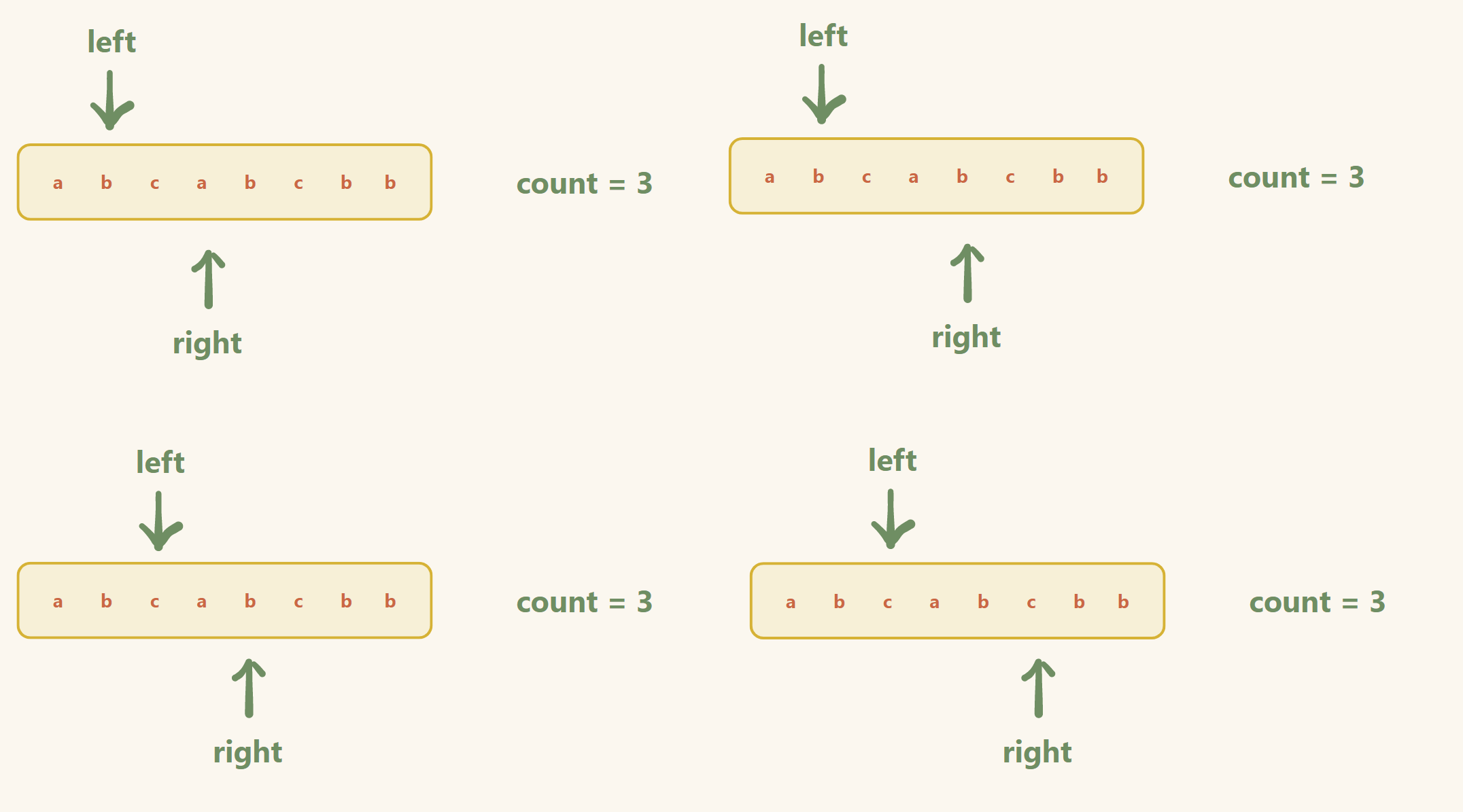
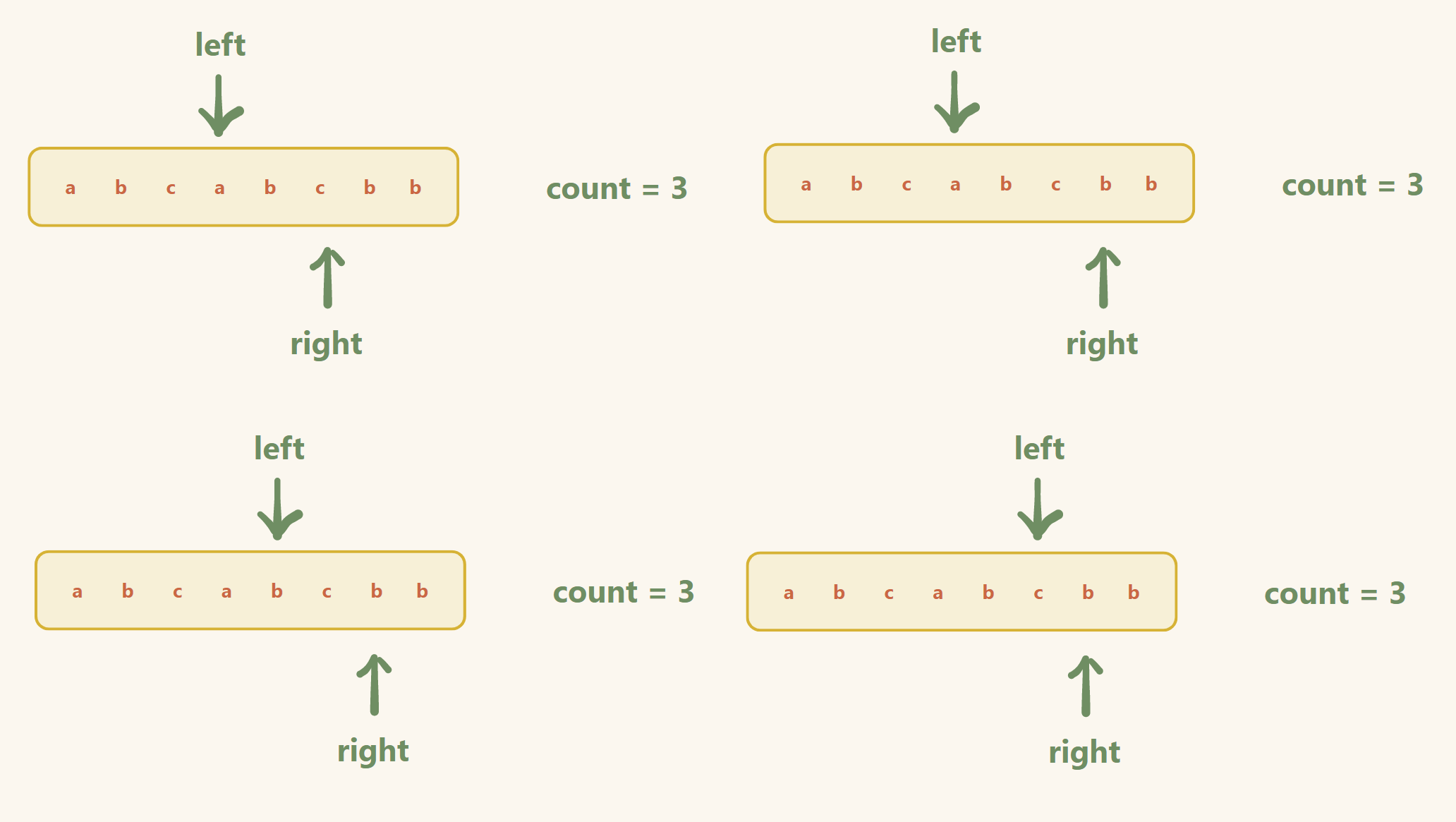
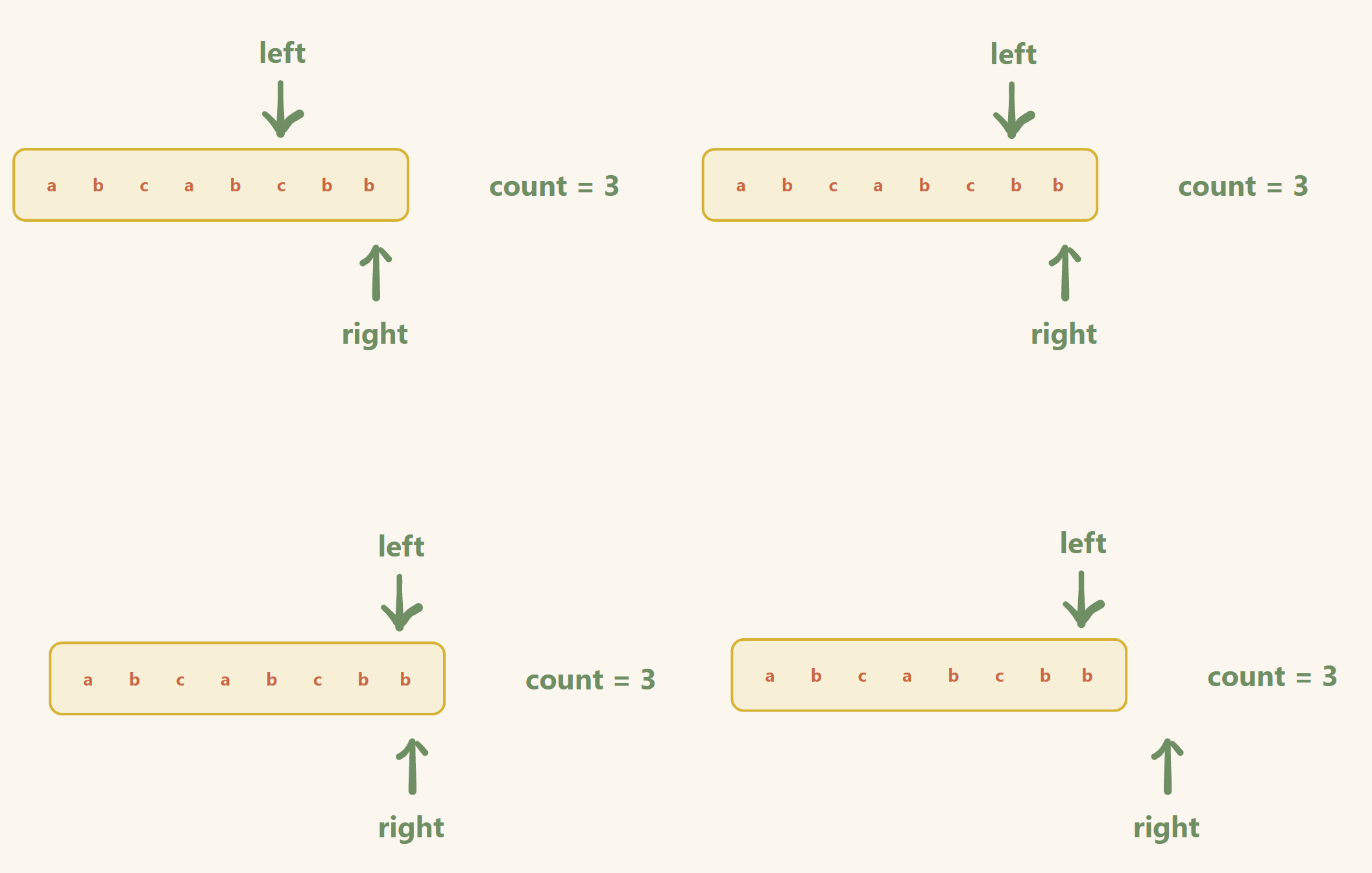
举例:(题解二的做法)
输入: s = "abcabcbb"
输出: 3
代码
class Solution {public: int lengthOfLongestSubstring(string s) { int n = 0; int hash[128] = {0}; int left = 0; int right = 0; while(right < s.size()) { hash[s[right]]++; if(hash[s[right]] == 2) { n = max(n,right - left); while(s[left] != s[right]) { hash[s[left]]--; left++; } hash[s[left]]--; left++; right++; } else { right++; } } n = max(n,(int)s.size() - left); return n; }};