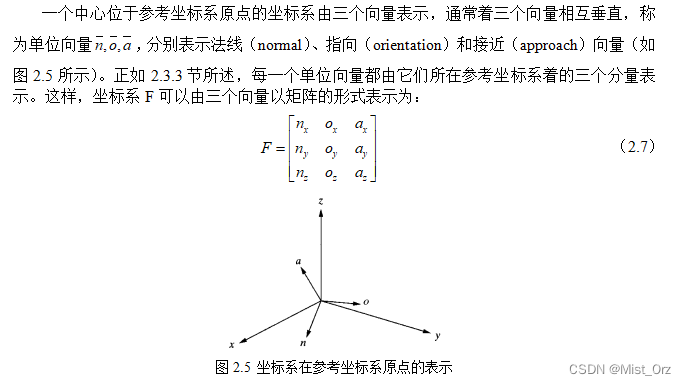
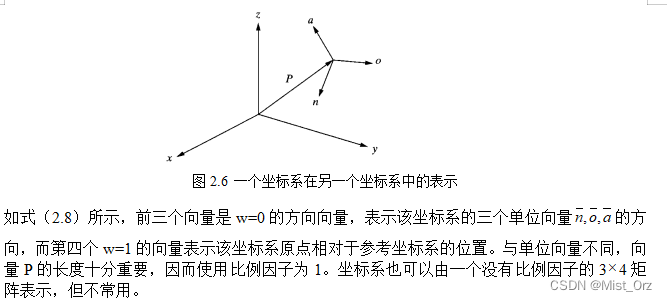
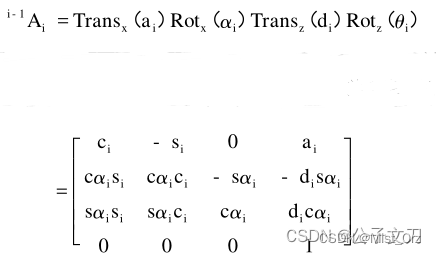文章目录
※ 参考资料整理建立DH模型△ 基本概念和标准DH/改进DH○ 连杆与关节的编号○ 标准DH与改进DH △ DH参数模型建立方法○ 标准DH参数定义及方法简介· 连杆坐标系建立方法· 标准DH参数含义※ 关于DH参数以哪个轴的指向为准的问题 ○ 改进DH参数定义及方法简介· 连杆坐标系建立方法· 改进DH参数含义※ 关于这里为什么是 a i − 1 a_{i-1} ai−1与 α i − 1 \alpha_{i-1} αi−1 ※ 关于DH参数的作用 △ ZK-500机器人DH建模过程及分析○ 机器人尺寸参数○ 标准DH(STD-DH)模型建立及验证· 标准DH模型建立过程· ZK-500机器人标准DH(STD-DH)参数· 验证标准DH模型参数 ○ 改进DH(M-DH)模型建立过程及验证· 改进DH模型建立过程※ 关于6杆的原点位置的选定 · ZK-500机器人改进DH(M-DH)参数· 验证改进DH模型参数 ※ 关于机器人的变换矩阵△ 空间变换的描述○ 欧拉角○ 四元数○ 齐次变换矩阵· 标准DH坐标系间的齐次变换矩阵· 改进DH坐标系间的齐次变换矩阵※ 关于齐次变换矩阵的意义※ 关于齐次变换矩阵的左乘/右乘 机器人正运动学△ 正运动学位姿描述矩阵△ 正运动学验证 机器人逆运动学机器人雅可比矩阵
关于机器人正逆解的原理、算法、代码什么的,在网上一找一大堆,其本身也是关于机器人的知识里面最基础的,其实没什么好写的,这里只是把我理解的内容整理一下,方便自己和需要的人查看。
另外这里要感谢赵而阳师弟,之前我在弄有限元分析的内容,把机器人相关的问题都丢给他了。
❤ 2023.6.6 ❤
※ 参考资料整理
关于机器人运动学的参考资料与文章挺多的,同时matlab实现机器人的正逆解有更简单的方法就是用“机器人工具箱(Robotics Toolbox)”,所以要说这里的资料是不是最好的最有价值的不一定,但至少有帮助吧。
首先是我之前整理的
→→→【Matlab机器人工具箱(Robotics Toolbox)学习笔记】
其实就是把B站一个将机器人工具箱的up的视频整理了一下,并且附上了自己的练习与验证内容
→→→【机器人标准DH建模与改进DH建模】
这篇文章用比较简练的语言和图形说明了标准DH和改进DH的区别
→→→【(3)机器人的DH参数建模详解】
这篇文章讲了我经常搞混的机器人关节和连杆的编号问题
→→→【【机械臂运动学教程】机械臂+旋转矩阵+变换矩阵+DH+逆解+轨迹规划+机器人+教程】
P4 4.机械臂几何法与DH表示法
→→→【工业六轴机器人常见的STD(标准)-DH模型建立方法】
→→→【SD-H模型运动学正解、逆解及姿态角的解算验证】
→→→【工业六轴机器人常见的MOD(改进)-DH模型建立方法】
→→→【MD-H模型运动学正解、逆解及姿态角的解算验证】
建立DH模型
这是由Danevit Harttnberg提出的故称为DH方法
关于机器人的DH建模的方法,在各种机器人参考书里都有,据说,外国的书用改进DH比较多,中国的书用标准DH比较多,其实我也没有仔细看过,但是根据我看过的书籍的内容,DH建模方法这部分都没有特别详细的讲解,可能是大家都觉得这个内容太基础了,没必要将这么详细吧。。。
总之,在最开始学习机器人时,大部分人对于该如何建立DH模型会感到很混乱,这里总结一下DH模型的建立方法。
首先是参考资料:
→→→【机器人标准DH建模与改进DH建模】
这篇文章用比较简练的语言和图形说明了标准DH和改进DH的区别
→→→【(3)机器人的DH参数建模详解】
这篇文章讲了我经常搞混的机器人关节和连杆的编号问题
△ 基本概念和标准DH/改进DH
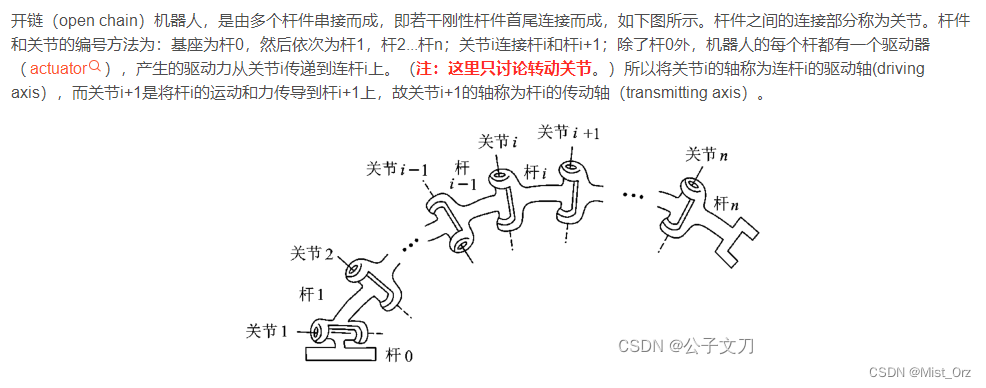
○ 连杆与关节的编号
这里直接引用【(3)机器人的DH参数建模详解】中的内容
总结一下,就是从基座为0开始,第几个杆编号就是几,离基座近的一端的关节编号和杆相同,远的一端编号+1
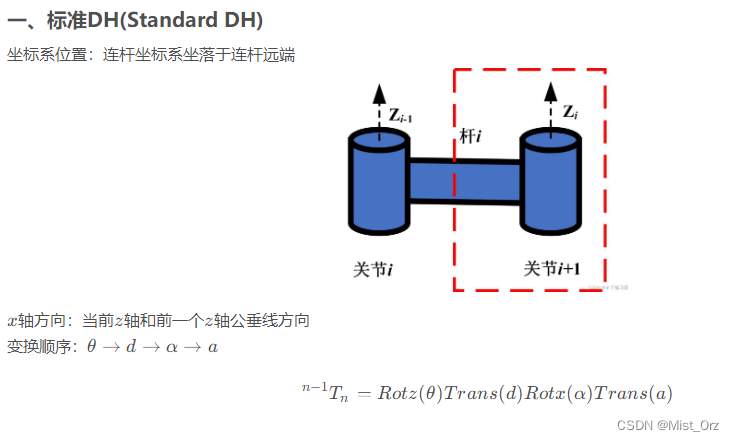
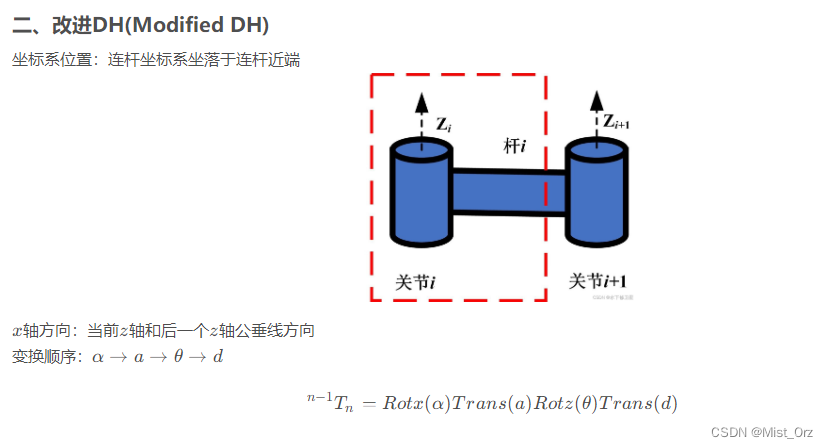
○ 标准DH与改进DH
标准DH与改进DH建立方法的区别这里引用【机器人标准DH建模与改进DH建模】:
总结一下:杆的坐标系建立在离底座远的一端的是标准DH,近的一端的是改进DH
标准DH与改进DH应用的区别简单来说就是当一个关节连了两个杆的时候,标准DH会出现歧义,而改进DH不会
△ DH参数模型建立方法
这里主要引用
→→→【(3)机器人的DH参数建模详解】中的内容
原文里各种公式崩了,这里我用Latex重新整理了一下
○ 标准DH参数定义及方法简介
· 连杆坐标系建立方法
第一步:确定各坐标系的Z轴:基本原则为:选取 z i z_{i} zi轴为关节i+1的轴向(如上面图片所示,如z1在轴2上)(指向可以任选,但是通常将各平行的Z轴的指向取为相同)。另外,机器人远端没有关节n+1,这时可以选取 z n z_{n} zn轴和 z n + 1 z_{n+1} zn+1轴重合 。
第二步:确定各坐标系的原点:基本原则为:选取原点 o i o_{i} oi在过 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi轴的公法线上(即公法线与 z i z_{i} zi轴的交点)。
注意:
① 当 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi轴平行时,两轴的公法线有无数条,若两轴重合则取 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1,若两轴平行且不重合则过 o i − 1 o_{i-1} oi−1点做两轴的公法线,此公法线与 z i z_{i} zi轴的交点即为 o i o_{i} oi。
② 由于没有 z − 1 z_{-1} z−1,故 o 0 o_{0} o0的无法按上面的方法确定,若 z 0 z_{0} z0与 z 1 z_{1} z1相交则 o 0 = o 1 o_{0}=o_{1} o0=o1,若 z 0 z_{0} z0与 z 1 z_{1} z1不相交取 o 0 o_{0} o0在 z 0 z_{0} z0与 z 1 z_{1} z1的公法线上。
基本原则为:选取 x i x_{i} xi轴沿过 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi 轴的公法线,方向从 z i − 1 z_{i-1} zi−1轴指向 z i z_{i} zi 轴。
注意:
① 当 z i − 1 z_{i-1} zi−1轴与 z i z_{i} zi 轴 重合时(这时 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1),选取 x i x_{i} xi轴满足在初始位置时 x i x_{i} xi轴与 x i − 1 x_{i-1} xi−1轴重合。
② 当 z i − 1 z_{i-1} zi−1轴与 z i z_{i} zi 轴相交且不重合时,选择 x i = ± ( z i − 1 × z i ) x_{i}=\pm (z_{i-1} \times z_{i}) xi=±(zi−1×zi)。通常使所有平行的X轴有相同的指向。
③ 当i=0时,由于 o 0 = o 1 o_{0}=o_{1} o0=o1或 o 0 o_{0} o0在 z 0 z_{0} z0与 z 1 z_{1} z1的公法线上,选取在初始位置时 x 0 x_{0} x0轴与 x 1 x_{1} x1轴重合。
基本原则为:使 y i = z i × x i y_{i}=z_{i}\times x_{i} yi=zi×xi构成右手坐标系。
· 标准DH参数含义
1、杆件长度 a i a_{i} ai:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的距离,沿 x i x_{i} xi轴的指向为正;
2、杆件扭角 α i \alpha_{i} αi:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的转角,绕 x i x_{i} xi轴正向转动为正,且 α i ∈ ( − π , π ] \alpha_i\in(-\pi,\pi] αi∈(−π,π];
3、关节距离 d i d_{i} di:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的距离,沿 z i − 1 z_{i-1} zi−1轴的指向为正;
4、关节扭角 θ i \theta_{i} θi:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的转角,绕 z i − 1 z_{i-1} zi−1轴正向转动为正,且 θ i ∈ ( − π , π ] \theta_i\in (-\pi,\pi] θi∈(−π,π];
※ 关于DH参数以哪个轴的指向为准的问题
这个问题我开始有点乱,为什么 a i a_{i} ai是以 x i x_{i} xi轴的指向为正而不是 x i − 1 x_{i-1} xi−1,而 d i d_{i} di就是以 z i − 1 z_{i-1} zi−1轴的指向为正而不是 z i z_{i} zi呢?
我想考了一下,我觉得这个是根据前面的建立各连杆的坐标系的方法决定的,其实抛开这些概念,将坐标系标在机器人结构图上就明白了,比如 a i a_{i} ai表示的是连杆长,也就是z轴间的距离,只有 x i x_{i} xi的方向才能表示出从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi的长度,于是才选定 x i x_{i} xi的方向为正。 d i d_{i} di同理
【!】这是我的理解,不知道是不是正确
○ 改进DH参数定义及方法简介
· 连杆坐标系建立方法
第一步:确定各坐标系的Z轴:基本原则为:选取 z i z_{i} zi轴为关节 i i i的轴向 。
第二步:确定各坐标系的原点:基本原则为:选取原点 o i o_{i} oi在过 z i z_{i} zi轴和 z i + 1 z_{i+1} zi+1轴的公法线上。
注意:
当 z i z_{i} zi轴和 z i + 1 z_{i+1} zi+1轴平行时,两轴的公法线有无数条,若两轴重合则取 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1(【???】这里存疑,我是按照标准DH写的),若两轴平行且不重合则过 o i − 1 o_{i-1} oi−1点做两轴的公法线,此公法线与 z i z_{i} zi轴的交点即为 o i o_{i} oi。
基本原则为:选取 x i x_{i} xi轴沿过 z i z_{i} zi轴和 z i + 1 z_{i+1} zi+1轴的公法线,方向从 z i z_{i} zi轴指向 z i + 1 z_{i+1} zi+1轴。
注意:
① 当 z i z_{i} zi轴与 z i + 1 z_{i+1} zi+1 轴 重合时(这时 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1),选取 x i x_{i} xi轴满足在初始位置时 x i x_{i} xi轴与 x i − 1 x_{i-1} xi−1轴重合。(【!!!】存疑,我是按照标准DH写的)
② 当 z i − 1 z_{i-1} zi−1轴与 z i z_{i} zi 轴相交且不重合时,选择 x i = ± ( z i − 1 × z i ) x_{i}=\pm (z_{i-1} \times z_{i}) xi=±(zi−1×zi)。通常使所有平行的X轴有相同的指向。
基本原则为:使 y i = z i × x i y_{i}=z_{i}\times x_{i} yi=zi×xi构成右手坐标系。
· 改进DH参数含义
1、杆件长度 a i − 1 a_{i-1} ai−1:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的距离,沿 x i − 1 x_{i-1} xi−1轴的指向为正;
2、杆件扭角 α i − 1 \alpha_{i-1} αi−1:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的转角,绕 x i − 1 x_{i-1} xi−1轴正向转动为正,且 α i ∈ ( − π , π ] \alpha_i\in (-\pi ,\pi ] αi∈(−π,π];
3、关节距离 d i d_i di:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的距离,沿 z i z_{i} zi轴的指向为正;
4、关节扭角 θ i \theta_i θi:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的转角,绕 z i z_{i} zi轴正向转动为正,且 θ i ∈ ( − π , π ] \theta_i\in (-\pi ,\pi ] θi∈(−π,π];
※ 关于这里为什么是 a i − 1 a_{i-1} ai−1与 α i − 1 \alpha_{i-1} αi−1
我的理解是,DH参数的作用是描述第 i {i} i个连杆的起始位置的参数,由于改进DH的坐标是建立在连杆的前端,也就是驱动轴上,那么能描述第 i {i} i个连杆的参数也就是该连杆的驱动轴与传动轴的距离(或者说关节偏置) d i d_i di(对于转动关节来说),以及第 i {i} i个连杆与第 i − 1 {i-1} i−1个连杆的相对位置的参数就是第 i − 1 {i-1} i−1个连杆的长度 a i − 1 a_{i-1} ai−1和夹角 α i − 1 \alpha_{i-1} αi−1。
如【机械臂运动学教程】机械臂+旋转矩阵+变换矩阵+DH+逆解+轨迹规划+机器人+教程视频中所示
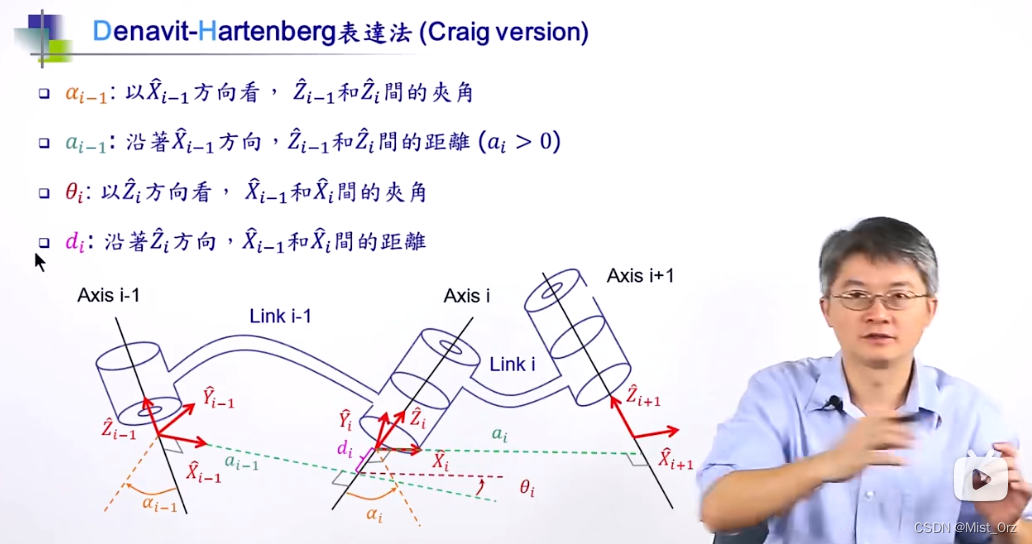
其实在用改进DH(M-DH)建立机器人模型时不需要考虑那么多,只要把连杆对应的这一行参数填进去就行。
※ 关于DH参数的作用
为什么需要四个DH参数,刚开始我还不太懂,后来看了这个视频,老师讲的很明白
→→→【【机械臂运动学教程】机械臂+旋转矩阵+变换矩阵+DH+逆解+轨迹规划+机器人+教程】
P4 4.机械臂几何法与DH表示法
用 a a a和 α \alpha α可以表示出同一个杆的驱动轴和传动轴之间的变化关系
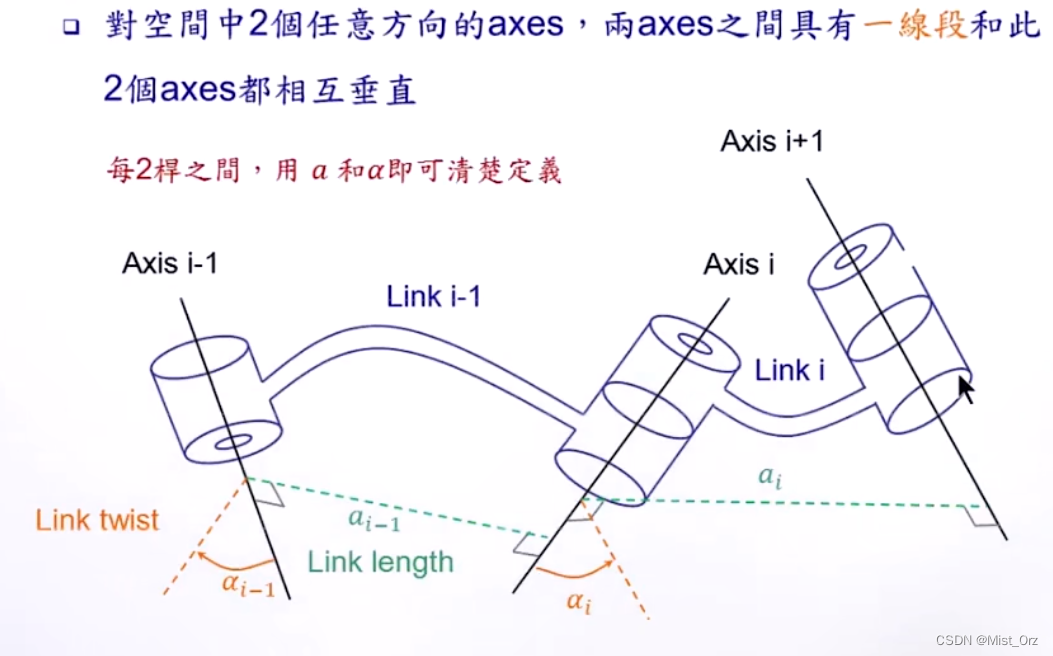
当有多个杆件串联时,需要 d d d和 θ \theta θ来表示两个杆件之间的相对位置关系
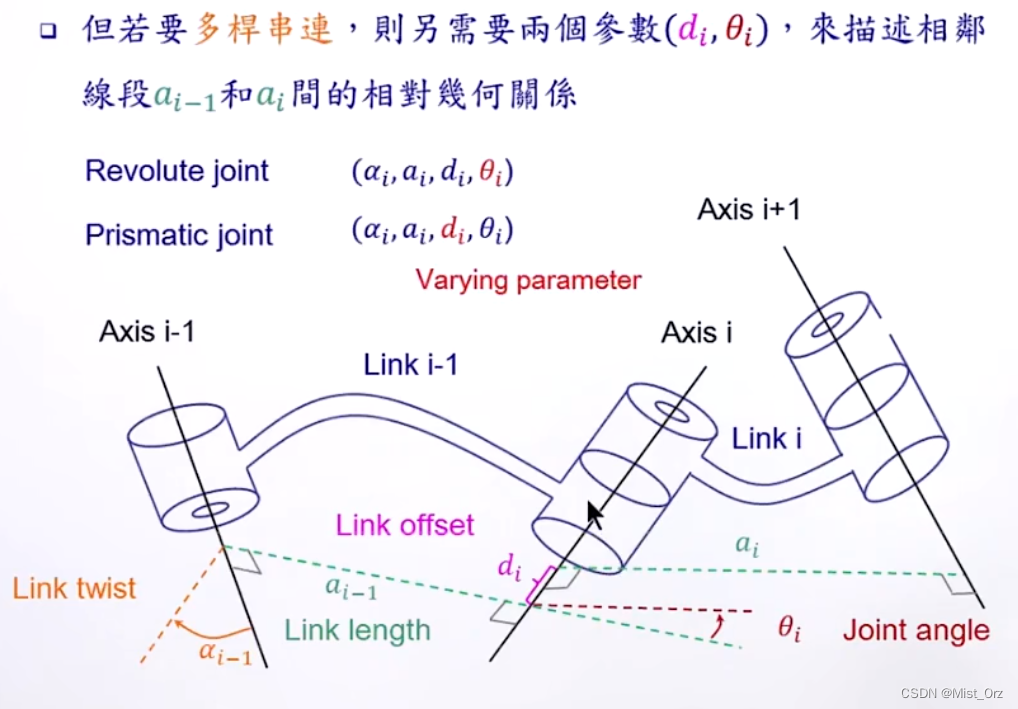
其中,在旋转关节中, θ \theta θ是变量,在平移关节中, d d d是变量
△ ZK-500机器人DH建模过程及分析
○ 机器人尺寸参数
这个机器人时南通振康生产的500Kg重载机器人(国产哦),现在用来做机器人搅拌摩擦焊的实验

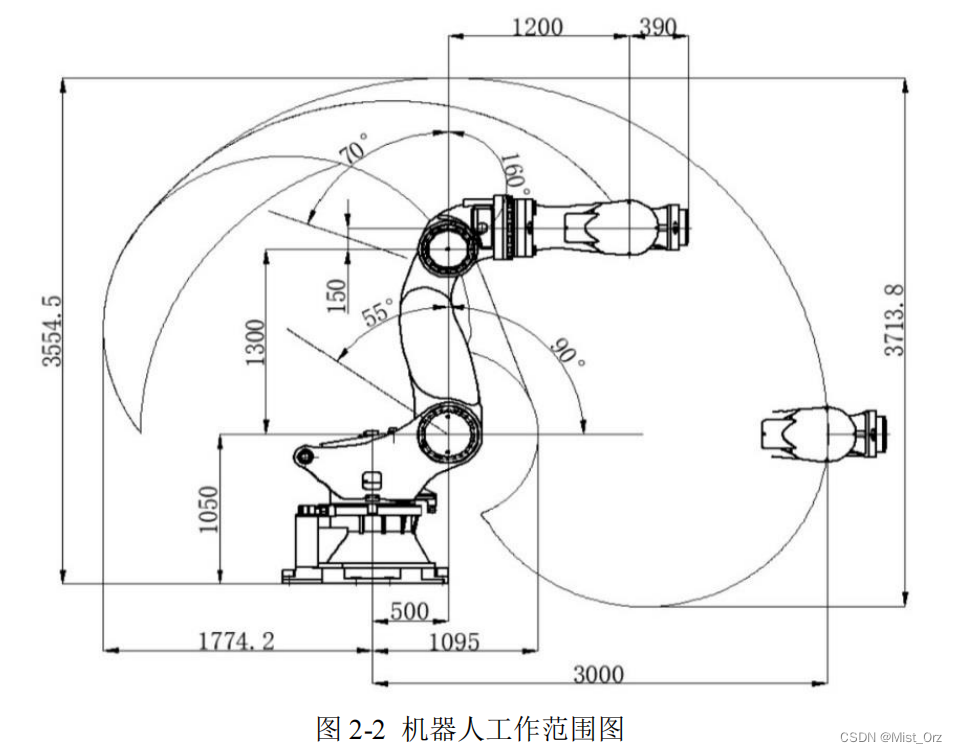
○ 标准DH(STD-DH)模型建立及验证
关于工业机器人标准DH(STD-DH)建模的参考结果可以见这篇文章
→→→【工业六轴机器人常见的STD(标准)-DH模型建立方法】
只是他的方法和我的z轴的方向不同
同时标准DH的正逆解验证也可以参考同一个作者的这篇文章
→→→【SD-H模型运动学正解、逆解及姿态角的解算验证】
· 标准DH模型建立过程
确定z轴方向基本原则为:选取 z i z_{i} zi轴为关节i+1的轴向(如上面图片所示,如z1在轴2上)(指向可以任选,但是通常将各平行的Z轴的指向取为相同)。另外,机器人远端没有关节n+1,这时可以选取 z n z_{n} zn轴和 z n + 1 z_{n+1} zn+1轴重合 。
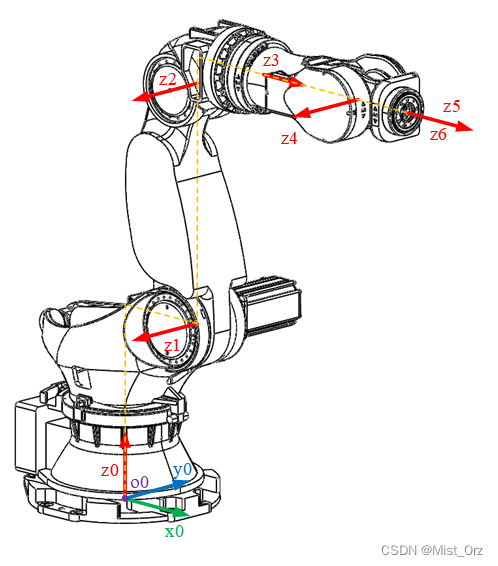
确定原点位置
基本原则为:选取原点 o i o_{i} oi在过 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi轴的公法线上(即公法线与 z i z_{i} zi轴的交点)。
注意:
① 当 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi轴平行时,两轴的公法线有无数条,若两轴重合则取 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1,若两轴平行且不重合则过 o i − 1 o_{i-1} oi−1点做两轴的公法线,此公法线与 z i z_{i} zi轴的交点即为 o i o_{i} oi。
② 由于没有 z − 1 z_{-1} z−1,故 o 0 o_{0} o0的无法按上面的方法确定,若 z 0 z_{0} z0与 z 1 z_{1} z1相交则 o 0 = o 1 o_{0}=o_{1} o0=o1,若 z 0 z_{0} z0与 z 1 z_{1} z1不相交取 o 0 o_{0} o0在 z 0 z_{0} z0与 z 1 z_{1} z1的公法线上。
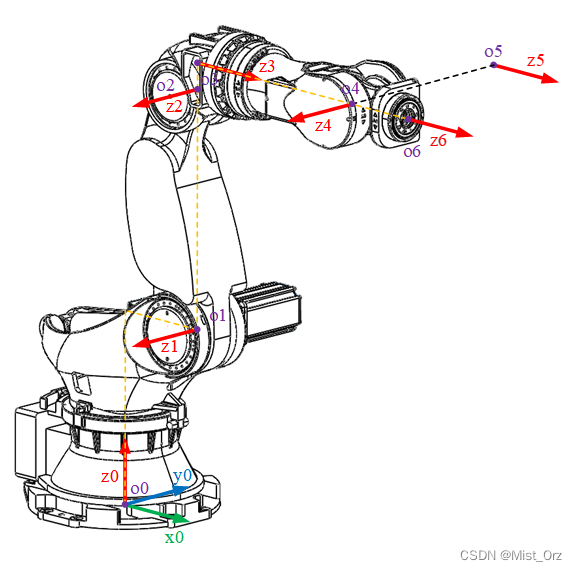
确定x轴方向
基本原则为:选取 x i x_{i} xi轴沿过 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi 轴的公法线,方向从 z i − 1 z_{i-1} zi−1轴指向 z i z_{i} zi 轴。
注意:
① 当 z i − 1 z_{i-1} zi−1轴与 z i z_{i} zi 轴 重合时(这时 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1),选取 x i x_{i} xi轴满足在初始位置时 x i x_{i} xi轴与 x i − 1 x_{i-1} xi−1轴重合。
② 当 z i − 1 z_{i-1} zi−1轴与 z i z_{i} zi 轴相交且不重合时,选择 x i = ± ( z i − 1 × z i ) x_{i}=\pm (z_{i-1} \times z_{i}) xi=±(zi−1×zi)。通常使所有平行的X轴有相同的指向。
③ 当i=0时,由于 o 0 = o 1 o_{0}=o_{1} o0=o1或 o 0 o_{0} o0在 z 0 z_{0} z0与 z 1 z_{1} z1的公法线上,选取在初始位置时 x 0 x_{0} x0轴与 x 1 x_{1} x1轴重合。
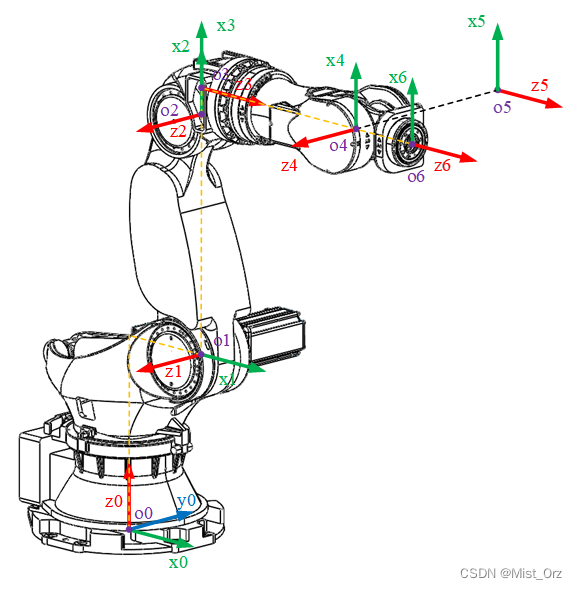
确定y轴方向
基本原则为:使 y i = z i × x i y_{i}=z_{i}\times x_{i} yi=zi×xi构成右手坐标系。
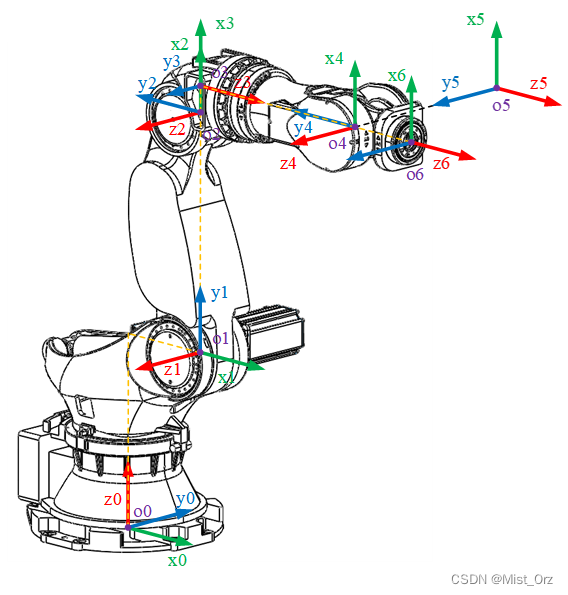
· ZK-500机器人标准DH(STD-DH)参数
1、杆件长度 a i a_{i} ai:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的距离,沿 x i x_{i} xi轴的指向为正;
2、杆件扭角 α i \alpha_{i} αi:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的转角,绕 x i x_{i} xi轴正向转动为正,且 α i ∈ ( − π , π ] \alpha_i\in(-\pi,\pi] αi∈(−π,π];
3、关节距离 d i d_{i} di:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的距离,沿 z i − 1 z_{i-1} zi−1轴的指向为正;
4、关节扭角 θ i \theta_{i} θi:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的转角,绕 z i − 1 z_{i-1} zi−1轴正向转动为正,且 θ i ∈ ( − π , π ] \theta_i\in (-\pi,\pi] θi∈(−π,π];
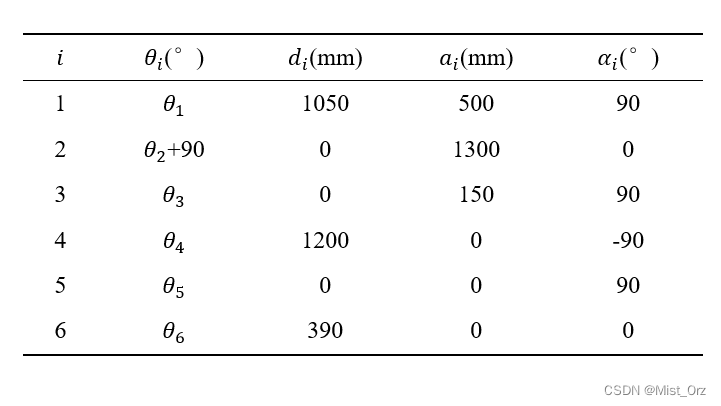
· 验证标准DH模型参数
使用matlab机器人工具箱验证标准DH模型
建立机器人模型
d1=1050;a1=500;a2=1300;a3=150;d4=1200;d6=390;% theta(z) d(z) a(x) alpha(x) L1=Link([ 0 d1 a1 pi/2 ],'standard');L2=Link([ 0 0 a2 0 ],'standard');L2.offset=pi/2;L3=Link([ 0 0 a3 pi/2 ],'standard');L4=Link([ 0 d4 0 -pi/2 ],'standard');L5=Link([ 0 0 0 pi/2 ],'standard');L6=Link([ 0 d6 0 0 ],'standard');Robot_6=SerialLink([L1,L2,L3,L4,L5,L6],'name','ZK-500');Robot_6.teach;注意这里的
L2.offset=pi/2;,是对应连杆2的90°的补偿,
运行结果
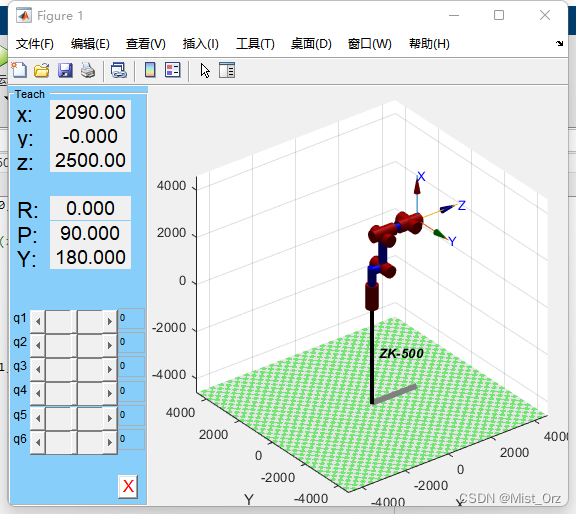
○ 改进DH(M-DH)模型建立过程及验证
关于工业机器人标准DH(STD-DH)建模的参考结果可以见这篇文章(和上面那篇同一个作者)
→→→【工业六轴机器人常见的MOD(改进)-DH模型建立方法】
只是他的方法和我的z轴的方向不同
同时改进DH的正逆解验证也可以参考同一个作者的这篇文章
→→→【MD-H模型运动学正解、逆解及姿态角的解算验证】
· 改进DH模型建立过程
确定z轴方向根据原则,选取 z i z_{i} zi轴为关节 i i i的轴向 。
确定各关节z轴方向如图所示:
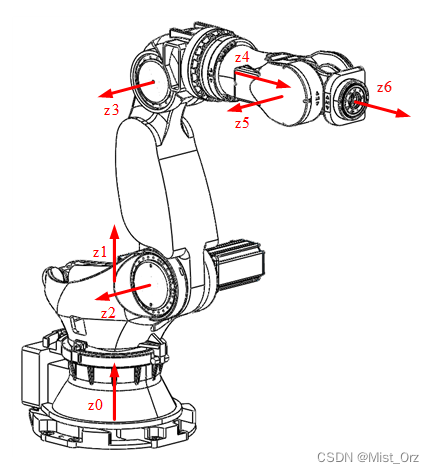
关于z轴方向的问题,理论上来说都可以,但是我看有的教程说要按照轴旋转的方向确定z轴的朝向,为此我还特地去查看了下机器人的各轴实际转动方向,但是转念一想,旋转方向如果实际和坐标不一致,那么只要在带入求解的时候加个负号就行了,但是如果在建立DH模型时就考虑方向,那么模型的通用型就会受到限制。
于是我决定按照:轴向沿竖直方向的轴(如1轴)方向向上,轴向沿水平方向的轴(如2、3、5轴)方向向外,轴向指向末端的轴(如4、6轴)方向指向末端的习惯来确定z轴的朝向。
确定原点位置
基本原则为:选取原点 o i o_{i} oi在过 z i z_{i} zi轴和 z i + 1 z_{i+1} zi+1轴的公法线上。
注意:
当 z i − 1 z_{i-1} zi−1轴和 z i z_{i} zi轴平行时,两轴的公法线有无数条,若两轴重合则取 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1(【!!!】存疑),若两轴平行且不重合则过 o i − 1 o_{i-1} oi−1点做两轴的公法线,此公法线与 z i z_{i} zi轴的交点即为 o i o_{i} oi。
按照以上原则,标注各连杆坐标系原点如图并适当平移了z轴的位置:
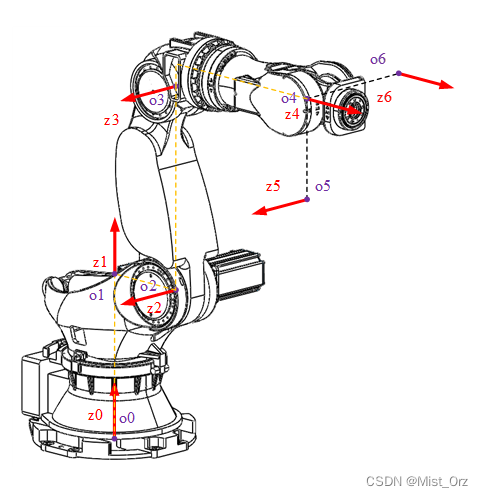
连杆4、5、6的坐标系的原点在同一个点,这里将5、6杆坐标系平移到不重叠的位置。
※ 关于6杆的原点位置的选定
按照传统的标准DH和改进DH模型,6杆的坐标原点都是应该建在机器人末端6轴的轴线位置的,但是如果将6杆的坐标原点移动到和4、5杆重合的位置,同时建立一个工具坐标系,将6杆的长度算作工具长度的一部分,则会大大简化逆解运算的复杂程度(听我师弟说的)。
原因我后面再讲(如果我写到后面能记起来的话。。。)
确定x轴方向
基本原则为:选取 x i x_{i} xi轴沿过 z i z_{i} zi轴和 z i + 1 z_{i+1} zi+1轴的公法线,方向从 z i z_{i} zi轴指向 z i + 1 z_{i+1} zi+1轴。
注意:
① 当 z i z_{i} zi轴与 z i + 1 z_{i+1} zi+1 轴 重合时(这时 o i = o i − 1 o_{i}=o_{i-1} oi=oi−1),选取 x i x_{i} xi轴满足在初始位置时 x i x_{i} xi轴与 x i − 1 x_{i-1} xi−1轴重合。(【!!!】存疑)
② 当 z i − 1 z_{i-1} zi−1轴与 z i z_{i} zi 轴相交且不重合时,选择 x i = ± ( z i − 1 × z i ) x_{i}=\pm (z_{i-1} \times z_{i}) xi=±(zi−1×zi)。通常使所有平行的X轴有相同的指向。
顺便标上了基座坐标系和工具坐标系
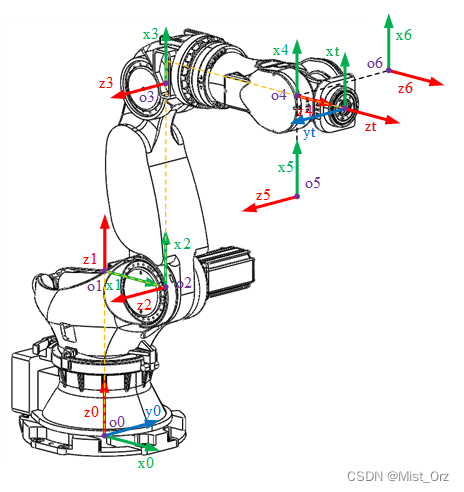
确定y轴方向
基本原则为:使 y i = z i × x i y_{i}=z_{i}\times x_{i} yi=zi×xi构成右手坐标系。
【更正(2023.12.2):经一位热心同学指出,我的y3方向标反了,大家脑补一下正确的结果,我就不改了诶嘿~】
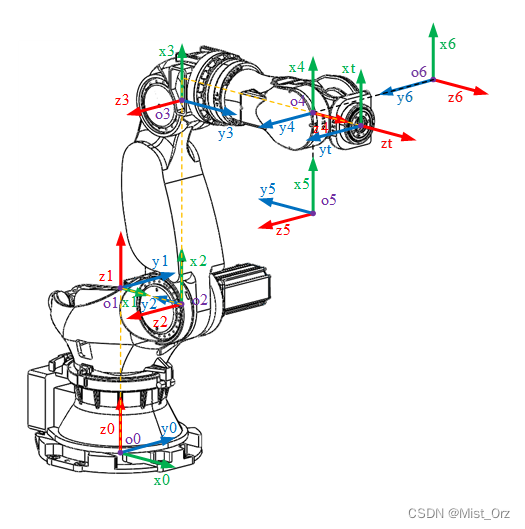
完成!
然后和大佬做的比较一下(其实我就是一边比较一边做的。。。)
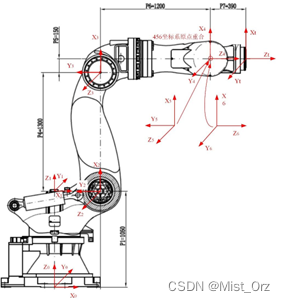
简直一模一样
· ZK-500机器人改进DH(M-DH)参数
1、杆件长度 a i − 1 a_{i-1} ai−1:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的距离,沿 x i − 1 x_{i-1} xi−1轴的指向为正;
2、杆件扭角 α i − 1 \alpha_{i-1} αi−1:定义为从 z i − 1 z_{i-1} zi−1轴到 z i z_{i} zi轴的转角,绕 x i − 1 x_{i-1} xi−1轴正向转动为正,且 α i ∈ ( − π , π ] \alpha_i\in (-\pi ,\pi ] αi∈(−π,π];
3、关节距离 d i d_i di:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的距离,沿 z i z_{i} zi轴的指向为正;
4、关节扭角 θ i \theta_i θi:定义为从 x i − 1 x_{i-1} xi−1轴到 x i x_{i} xi轴的转角,绕 z i z_{i} zi轴正向转动为正,且 θ i ∈ ( − π , π ] \theta_i\in (-\pi ,\pi ] θi∈(−π,π];
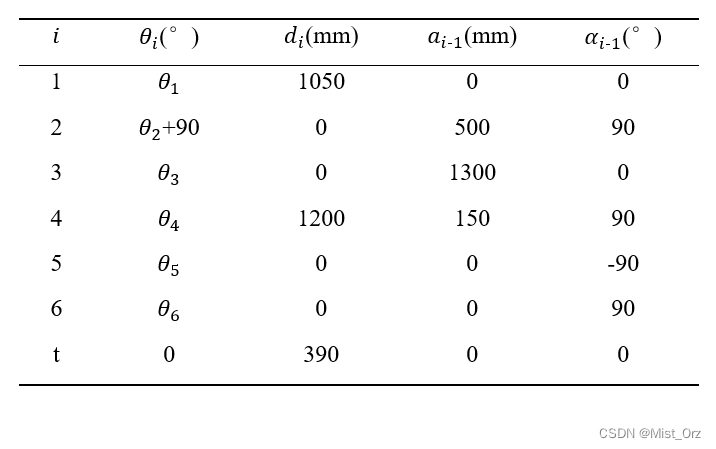
· 验证改进DH模型参数
使用matlab机器人工具箱验证改进DH模型
建立机器人模型
d1=1050;a1=500;a2=1300;a3=150;d4=1200;d6=390;% theta(z) d(z) a(x) alpha(x) L1=Link([ 0 d1 0 0 ],'modified');L2=Link([ 0 0 a1 pi/2 ],'modified');L2.offset=pi/2;L3=Link([ 0 0 a2 0 ],'modified');L4=Link([ 0 d4 a3 pi/2 ],'modified');L5=Link([ 0 0 0 -pi/2 ],'modified');L6=Link([ 0 d6 0 pi/2 ],'modified');Robot_6=SerialLink([L1,L2,L3,L4,L5,L6],'name','ZK-500');Robot_6.teach;这里没有完全按照上面的表格来配置参数,也就是没有将杆6的偏置作为工具的长度,而是按照一般的方法将其带入了杆6的参数
结果如下
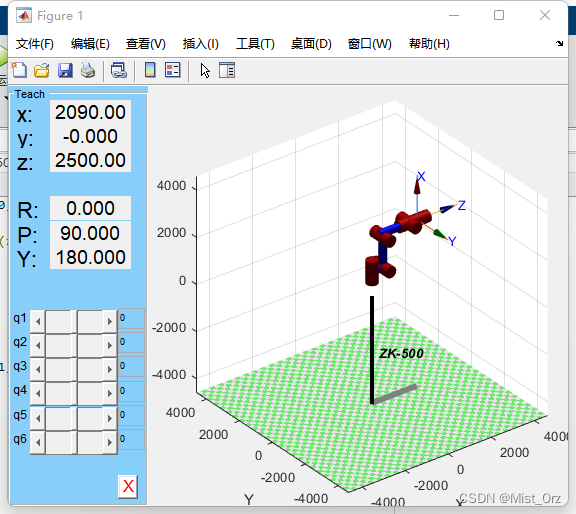
虽然长得有点奇怪,但是拖动了一下各个轴,结果还是比较正常的。
OK,至此完成了ZK-500机器人的DH建模
❤ 2023.6.14 ❤
※ 关于机器人的变换矩阵
在总结机器人的正逆运动学之前先简单介绍下机器人的变换矩阵。
其实之前学习相关内容的时候都是当做定义来记的,但是整理资料的时候发现里面忽略的内容还不少,这里就简单记录一下。
参考的资料如下:
→→→【关于机器人运动学中变换矩阵左乘右乘的理解】
作者以他自己的理解说明了变换矩阵左乘与右乘的区别与联系
→→→【如何通俗地解释欧拉角?之后为何要引入四元数?】
这是篇讲解欧拉角的文章,突出一个通俗和简单易懂
→→→【三维旋转之欧拉角】
这篇文章同样比较通俗的讲解了欧拉角的概念,同时给出了欧拉角旋转顺序的12钟不同组合
△ 空间变换的描述
○ 欧拉角
欧拉角的定义很简单,就是绕xyz三个轴旋转,旋转矩阵的推导也很简单

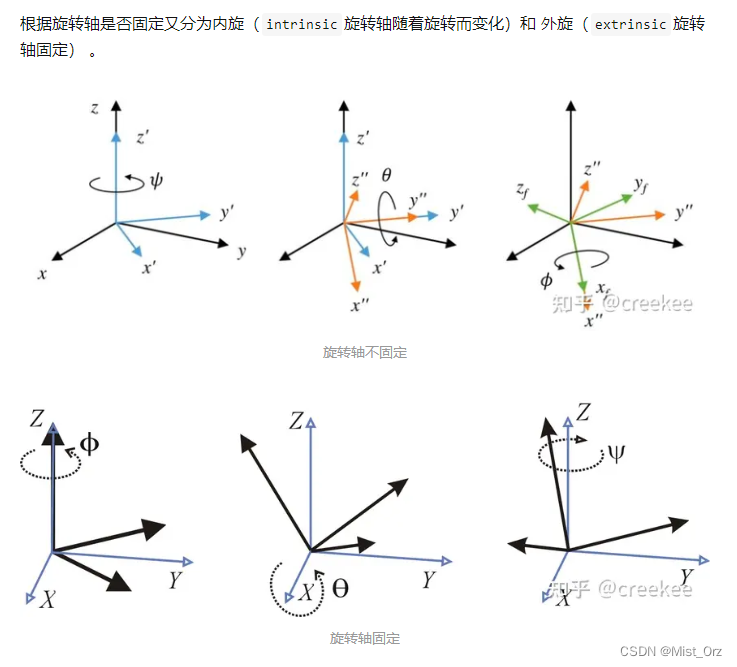
但是用欧拉角来描述一个物体的旋转运动会有不同的情况
旋转矩阵的左乘/右乘与外旋/内旋根据【关于机器人运动学中变换矩阵左乘右乘的理解】的描述,左乘旋转矩阵是坐标系不动,即外旋;右乘旋转矩阵是坐标系随着旋转而变化,即内旋
【三维旋转之欧拉角】中的描述如下
欧拉角的旋转顺序
引用【如何通俗地解释欧拉角?之后为何要引入四元数?】中的内容:
如下图所示,xyz表示世界坐标系,XYZ表示物体局部坐标系,
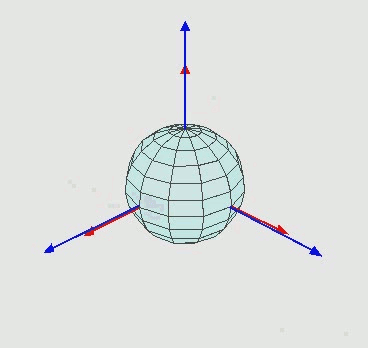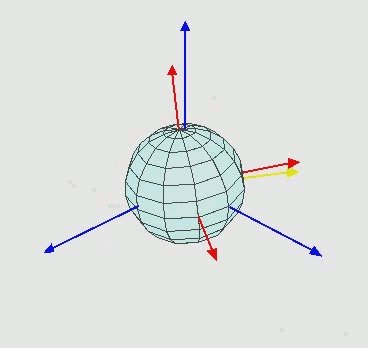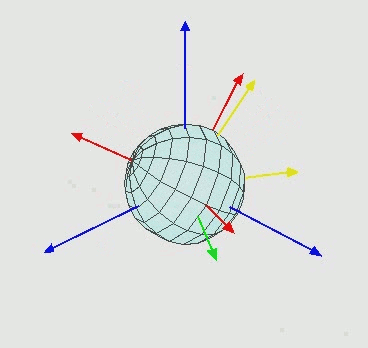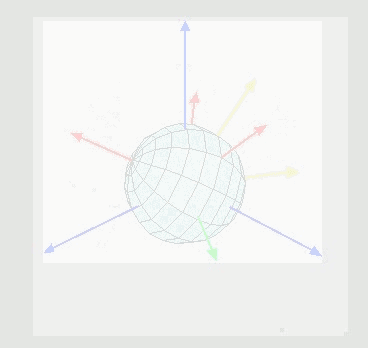
将上图的运动进行分解
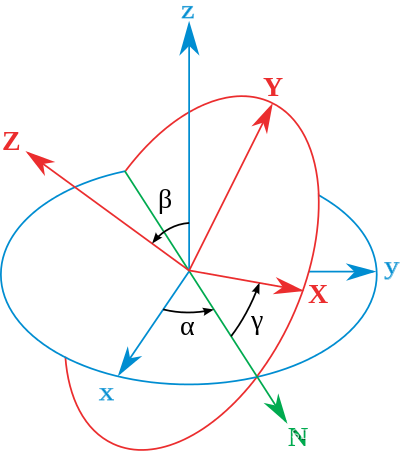

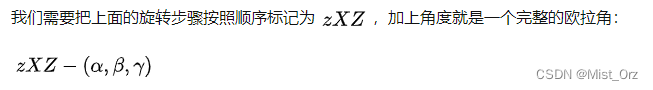
这是其中一种欧拉角的描述方法,根据不同的旋转顺序,一共有12种不同的描述方法,对应的旋转矩阵也不同
【三维旋转之欧拉角】记录如下
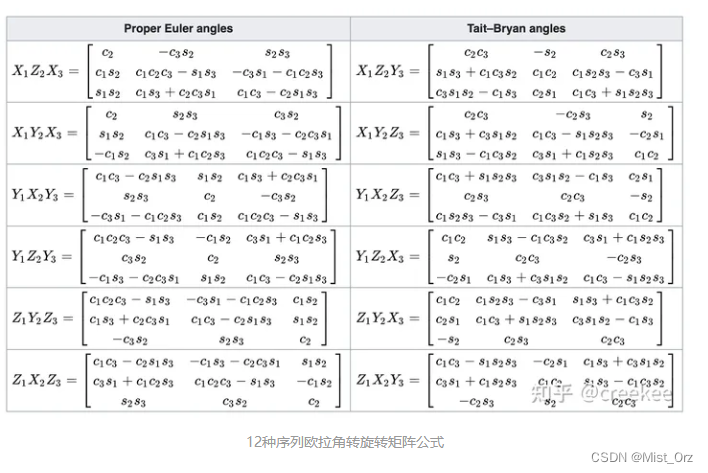
欧拉角描述存在的问题
用欧拉角描述一个旋转变换会出现“万向节锁死”的情况
具体还是看这里【如何通俗地解释欧拉角?之后为何要引入四元数?】
○ 四元数
关于什么是四元数,这是一个很复杂的数学概念,可以参考
→→→【四元数——基本概念】
这篇文章讲的还是比较通俗易懂的(但是我依然没看懂。。。)
→→→【带你探秘四维的神秘数字——四元数】
这是一个国内up的视频
→→→【四元数的可视化】——3Blue1Brown
这是一个外国的著名的讲解各种数学问题的账号
emmm。。。看了之后我就觉得。。。以后用到了再看吧。。。
○ 齐次变换矩阵
齐次变换矩阵就是把旋转矩阵与平移矩阵写在一个矩阵里
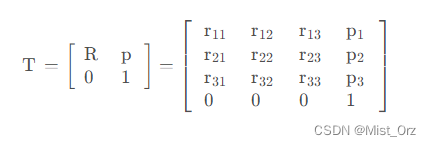
齐次变换矩阵也可以写成这样的形式
T = [ n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 ] T=\left[\begin{matrix}n_x&o_x&a_x&p_x\\n_y&o_y&a_y&p_y\\n_z&o_z&a_z&p_z\\0&0&0&1\\\end{matrix}\right] T= nxnynz0oxoyoz0axayaz0pxpypz1
其中旋转矩阵
R = [ n x o x a x n y o y a y n z o z a z ] R=\left[\begin{matrix}n_x&o_x&a_x\\n_y&o_y&a_y\\n_z&o_z&a_z\\\end{matrix}\right] R= nxnynzoxoyozaxayaz
中的列向量表示如下含义
→→→《机器人运动学精品教程》
如果一个坐标系除了有旋转变换还有平移变换时
· 标准DH坐标系间的齐次变换矩阵
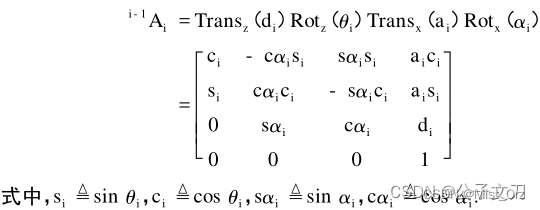
· 改进DH坐标系间的齐次变换矩阵
【 !!】以下这个变换矩阵是【(3)机器人的DH参数建模详解】这篇文章中给出的变换矩阵,但是根据前面的改进DH建模的定义,这里的 a i a_{i} ai和 α i \alpha_{i} αi应该为 a i − 1 a_{i-1} ai−1和 α i − 1 \alpha_{i-1} αi−1
改正后的坐标系间齐次变换矩阵(这个是《机器人学、机器视觉与控制》的内容,不会有错的!)
i i − 1 A = R x ( α i − 1 ) T x ( a i − 1 ) R z ( θ i ) T z ( d i ) = [ c θ i − s θ i 0 a i − 1 s θ i c α i − 1 c θ i c α i − 1 − s α i − 1 − s α i − 1 d i s θ i s α i − 1 c θ i s α i − 1 c α i − 1 c α i − 1 d i 0 0 0 1 ] \begin{aligned}\ _i^{i-1}A&=R_x\left(\alpha_{i-1}\right)T_x\left(a_{i-1}\right)R_z\left(\theta_i\right)T_z\left(d_i\right)\\&=\left[\begin{matrix}c\theta_i&-s\theta_i&0&a_{i-1}\\s\theta_ic\alpha_{i-1}&c\theta_ic\alpha_{i-1}&-s\alpha_{i-1}&-s\alpha_{i-1}d_i\\s\theta_is\alpha_{i-1}&c\theta_is\alpha_{i-1}&c\alpha_{i-1}&c\alpha_{i-1}d_i\\0&0&0&1\\\end{matrix}\right]\end{aligned} ii−1A=Rx(αi−1)Tx(ai−1)Rz(θi)Tz(di)= cθisθicαi−1sθisαi−10−sθicθicαi−1cθisαi−100−sαi−1cαi−10ai−1−sαi−1dicαi−1di1
【!!】关于 【标准DH和改进DH的坐标系间的齐次变换矩阵为什么是这样定义的呢?】
我也很疑惑,但是根据我在《机器人学、机器视觉与控制》这本书P156看到的内容,这个是发明和改进DH建模方法的大佬规定的。。。
※ 关于齐次变换矩阵的意义
齐次变换矩阵是对两个坐标系相对位置的描述。
可以理解成坐标系 o i − 1 o_{i-1} oi−1经过齐次变换矩阵 i i − 1 T {_i^{i-1}}T ii−1T得到 o i o_{i} oi。 i i − 1 T {_i^{i-1}}T ii−1T为坐标系 o i o_{i} oi在坐标系 o i − 1 o_{i-1} oi−1中的表示。
下面通过一个简单的例子来说明如下图坐标系,假设z方向的距离和转角都为零,将空间变换转化为平面坐标中表示
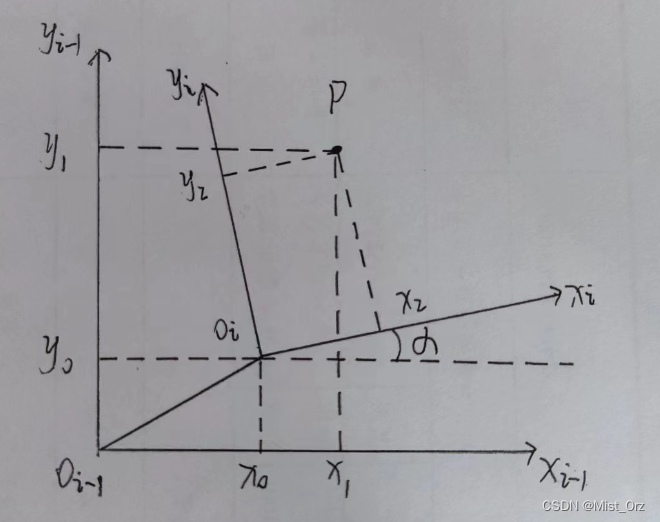
这两个坐标系间的齐次变换矩阵为
i i − 1 T = [ cos α − sin α 0 x 0 sin α cos α 0 y 0 0 0 1 0 0 0 0 1 ] \ {_i^{i-1}}T=\left[\begin{matrix}\cos{\alpha}&-\sin{\alpha}&0&x_0\\\sin{\alpha}&\cos{\alpha}&0&y_0\\0&0&1&0\\0&0&0&1\\\end{matrix}\right]\ ii−1T= cosαsinα00−sinαcosα000010x0y001
此时在 o i − 1 o_{i-1} oi−1中有一点 P P P,他在坐标系 o i − 1 o_{i-1} oi−1中的坐标向量为 p i − 1 → = [ x 1 y 1 0 ] T \overrightarrow{p_{i-1}}=[\begin{matrix}x_1&y_1&0\end{matrix}]^{\mathrm{T}} pi−1 =[x1y10]T,要想得到他在变换后的坐标系 o i o_{i} oi中的坐标向量 p i → [ x 2 y 2 0 ] T \overrightarrow{p_{i}}[\begin{matrix}x_2&y_2&0\end{matrix}]^{\mathrm{T}} pi [x2y20]T
此时两个向量坐标之间的变化关系为
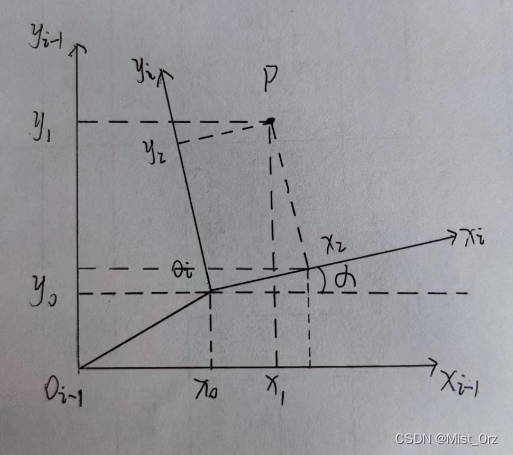
{ x 1 = x 2 cos α − y 2 sin α + x 0 y 1 = x 2 sin α + y 2 cos α + y 0 \left\{\begin{matrix}x_1=x_2\cos{\alpha}-y_2\sin{\alpha}+x_0\\y_1=x_2\sin{\alpha}+y_2\cos{\alpha}+y_0\\\end{matrix}\right. {x1=x2cosα−y2sinα+x0y1=x2sinα+y2cosα+y0
写成矩阵相乘的形式
[ x 1 y 1 z 1 1 ] = [ cos α − sin α 0 x 0 sin α cos α 0 y 0 0 0 1 0 0 0 0 1 ] [ x 2 y 2 z 2 1 ] \left[\begin{matrix}x_1\\y_1\\z_1\\1\\\end{matrix}\right]=\left[\begin{matrix}\cos{\alpha}&-\sin{\alpha}&0&x_0\\\sin{\alpha}&\cos{\alpha}&0&y_0\\0&0&1&0\\0&0&0&1\\\end{matrix}\right]\left[\begin{matrix}x_2\\y_2\\z_2\\1\\\end{matrix}\right] x1y1z11 = cosαsinα00−sinαcosα000010x0y001 x2y2z21
可以发现,这个向量变化关系可以写成
p i → = i i − 1 T ⋅ p i − 1 → \overrightarrow{p_{i}}={_i^{i-1}}T\cdot\overrightarrow{p_{i-1}} pi =ii−1T⋅pi−1
于是可以认为 【齐次变换矩阵与变换后的坐标矩阵相乘,可以得到变换前的坐标】。
如果此时坐标向量为机器人末端点在工具坐标系中的位置向量,那么将此向量依次左乘机器人从末端到基座的齐次变换矩阵,则会得到末端点在机器人基座坐标系中的坐标向量。
p 0 → = 1 0 T 2 1 T 3 2 T 4 3 T 5 4 T 6 5 T t 6 T ⋅ p t → = t 0 T ⋅ p t → \overrightarrow{p_{0}}={_1^{0}}T{\ }{_2^{1}}T{\ }{_3^{2}}T{\ }{_4^{3}}T{\ }{_5^{4}}T{\ }{_6^{5}}T{\ }{_t^{6}}T\cdot\overrightarrow{p_{t}}={_t^{0}}T\cdot\overrightarrow{p_{t}} p0 =10T 21T 32T 43T 54T 65T t6T⋅pt =t0T⋅pt
此时 6 0 T {_6^{0}}T 60T即为机器人的齐次变换矩阵
t 0 T = 1 0 T 2 1 T 3 2 T 4 3 T 5 4 T 6 5 T t 6 T {_t^{0}}T={_1^{0}}T{\ }{_2^{1}}T{\ }{_3^{2}}T{\ }{_4^{3}}T{\ }{_5^{4}}T{\ }{_6^{5}}T{\ }{_t^{6}}T t0T=10T 21T 32T 43T 54T 65T t6T
【!!】齐次变换矩阵 i i − 1 T {_i^{i-1}}T ii−1T表示的意义是连杆坐标系 o i o_i oi在连杆坐标系 o i − 1 o_{i-1} oi−1中的描述
见→→→【齐次变换矩阵相乘的物理意义(欧拉角的矩阵相乘顺序)】
※ 关于齐次变换矩阵的左乘/右乘
简单来说,从数学上来说,左乘是对原矩阵进行行变换,右乘进行列变换;从变换矩阵的角度来说,左乘旋转矩阵绕固定坐标系旋转,右乘旋转矩阵绕自身坐标系旋转.
但是单纯的这样理解很容易让人误解。
我在查阅了很多资料后,发现这篇文章讲的比较清楚详细
→→→【旋转矩阵及左右乘的意义,看这一篇就够了】
文章比较长,我就不搬了,需要的同学自己跳转哈~
机器人正运动学
考虑到我看到的资料里大部分的分析都是在改进DH模型基础上进行的,所以这里我只用改进DH方法
还有一个原因,matlab机器人工具箱针对标准DH方法建立的机器人模型有预设的求逆解得函数,但是改进DH的求逆解函数并不能用(至少我之前学的时候是这样的),需要自己写。
△ 正运动学位姿描述矩阵
首先根据坐标系间的齐次变换矩阵,推导出完整的机器人的齐次变换矩阵。
1 0 T = [ c 1 − s 1 0 0 s 1 c 1 0 0 0 0 1 d 1 0 0 0 1 ] \ {_1^0}T=\left[\begin{matrix}c_1&-s_1&0&0\\s_1&c_1&0&0\\0&0&1&d_1\\0&0&0&1\\\end{matrix}\right]\ 10T= c1s100−s1c100001000d11
2 1 T = [ c 2 − s 2 0 a 1 0 0 − 1 0 s 2 c 2 0 0 0 0 0 1 ] {_2^1}T=\left[\begin{matrix}c_2&-s_2&0&a_1\\0&0&-1&0\\s_2&c_2&0&0\\0&0&0&1\\\end{matrix}\right] 21T= c20s20−s20c200−100a1001
3 2 T = [ c 3 − s 3 0 a 2 s 3 c 3 0 0 0 0 1 0 0 0 0 1 ] {_3^2}T=\left[\begin{matrix}c_3&-s_3&0&a_2\\s_3&c_3&0&0\\0&0&1&0\\0&0&0&1\\\end{matrix}\right] 32T= c3s300−s3c3000010a2001
4 3 T = [ c 4 − s 4 0 a 3 0 0 − 1 − d 4 s 4 c 4 0 0 0 0 0 1 ] {_4^3}T=\left[\begin{matrix}c_4&-s_4&0&a_3\\0&0&-1&-d_4\\s_4&c_4&0&0\\0&0&0&1\\\end{matrix}\right] 43T= c40s40−s40c400−100a3−d401
5 4 T = [ c 5 − s 5 0 0 0 0 1 0 − s 5 − c 5 0 0 0 0 0 1 ] {_5^4}T=\left[\begin{matrix}c_5&-s_5&0&0\\0&0&1&0\\-s_5&-c_5&0&0\\0&0&0&1\\\end{matrix}\right] 54T= c50−s50−s50−c5001000001
6 5 T = [ c 6 − s 6 0 0 0 0 − 1 0 s 6 c 6 0 0 0 0 0 1 ] {_6^5}T=\left[\begin{matrix}c_6&-s_6&0&0\\0&0&-1&0\\s_6&c_6&0&0\\0&0&0&1\\\end{matrix}\right] 65T= c60s60−s60c600−1000001
t 6 T = [ 1 0 0 0 0 1 0 0 0 0 1 d t 0 0 0 1 ] {_t^6}T=\left[\begin{matrix}1&0&0&0\\0&1&0&0\\0&0&1&d_t\\0&0&0&1\\\end{matrix}\right] t6T= 10000100001000dt1
matlab代码syms Q1 Q2 Q3 Q4 Q5 Q6 d1 d4 dt a1 a2 a3 %ZK-500连杆间齐次变换矩阵T_01 =[ cos(Q1), -sin(Q1), 0, 0 sin(Q1), cos(Q1), 0, 0 0, 0, 1, d1 0, 0, 0, 1];T_12 =[ cos(Q2), -sin(Q2), 0, a1 0, 0, -1, 0 sin(Q2), cos(Q2), 0, 0 0, 0, 0, 1];T_23 =[ cos(Q3), -sin(Q3), 0, a2 sin(Q3), cos(Q3), 0, 0 0, 0, 1, 0 0, 0, 0, 1];T_34 =[ cos(Q4), -sin(Q4), 0, a3 0, 0, -1, -d4 sin(Q4), cos(Q4), 0, 0 0, 0, 0, 1];T_45 =[ cos(Q5), -sin(Q5), 0, 0 0, 0, 1, 0 -sin(Q5), -cos(Q5), 0, 0 0, 0, 0, 1];T_56 =[ cos(Q6), -sin(Q6), 0, 0 0, 0, -1, 0 sin(Q6), cos(Q6), 0, 0 0, 0, 0, 1];T_6t=[ 1 0 0 0 0 1 0 0 0 0 1 dt 0 0 0 1];由于连杆间的齐次变换矩阵表示的是后一个坐标系在前一个坐标系中的表示(如 1 0 T {_1^0}T 10T表示的时杆1的坐标系在基座坐标系中的表示),于是将机器人各连杆间的齐次变换矩阵按从末端到基座的顺序连续左乘,即可得到末端相对于基座坐标系的位姿描述矩阵。
工具坐标系与杆6坐标系转角保持不变,只是沿 z 6 z_6 z6轴平移一定距离,在计算机器人整体齐次变换矩阵时不计算在内。
但是注意因为建立机器人改进DH模型时将4、5、6连杆的坐标系原点重合,因此连杆6的长度也被视为末端工具长度的一部分。
6 0 T = 1 0 T 2 1 T 3 2 T 4 3 T 5 4 T 6 5 T = [ n x o x a x p x n y o y a y p y n z o z a z p z 0 0 0 1 ] {_6^0}T={{_1^0}T\ }_2^1{T\ }_3^2{T\ }_4^3{T\ }_5^4{T\ }_6^5T=\left[\begin{matrix}n_x&o_x&a_x&p_x\\n_y&o_y&a_y&p_y\\n_z&o_z&a_z&p_z\\0&0&0&1\\\end{matrix}\right] 60T=10T 21T 32T 43T 54T 65T= nxnynz0oxoyoz0axayaz0pxpypz1
其中各项元素为:
(简化表示: s 1 = sin θ 1 s_1=\sin{\theta_1} s1=sinθ1, c 1 = cos θ 1 c_1=\cos{\theta_1} c1=cosθ1, s 23 = sin ( θ 2 + θ 3 ) s_{23}=\sin{\left(\theta_2+\theta_3\right)} s23=sin(θ2+θ3), c 23 = cos ( θ 2 + θ 3 ) c_{23}=\cos{\left(\theta_2+\theta_3\right)} c23=cos(θ2+θ3))
n x = s 6 ( c 4 s 1 − s 4 c 1 c 23 ) − c 6 ( s 5 c 1 s 23 − c 5 ( s 1 s 4 + c 4 c 1 c 23 ) ) n y = − c 6 ( s 5 s 1 s 23 + c 5 ( c 1 s 4 − c 4 s 1 c 23 ) ) − s 6 ( c 1 c 4 + s 4 s 1 c 23 ) n z = c 6 ( s 5 c 23 + c 4 c 5 s 23 ) − s 4 s 6 s 23 o x = s 6 ( s 5 c 1 s 23 − c 5 ( s 1 s 4 + c 4 c 1 c 23 ) ) + c 6 ( c 4 s 1 − s 4 c 1 c 23 ) o y = s 6 ( s 5 s 1 s 23 + c 5 ( c 1 s 4 − c 4 s 1 c 23 ) ) − c 6 ( c 1 c 4 + s 4 s 1 c 23 ) o z = − s 6 ( s 5 c 23 + c 4 c 5 s 23 ) − c 6 s 4 s 23 a x = c 5 c 1 s 23 + s 5 ( s 1 s 4 + c 4 c 1 c 23 ) a y = c 5 s 1 s 23 − s 5 ( c 1 s 4 − c 4 s 1 c 23 ) a z = c 4 s 5 s 23 − c 5 c 23 p x = a 1 c 1 + a 3 c 1 c 23 + d 4 c 1 s 23 + a 2 c 1 c 2 p y = a 1 s 1 + a 3 s 1 c 23 + d 4 s 1 s 23 + a 2 c 2 s 1 p z = d 1 + a 2 s 2 + a 3 s 23 − d 4 c 23 \begin{aligned} n_x&=s_6\left(c_4s_1-s_4c_1c_{23}\right)-c_6\left(s_5c_1s_{23}-c_5\left(s_1s_4+c_4c_1c_{23}\right)\right)\ \\ n_y&=-c_6\left(s_5s_1s_{23}\ +\ c_5\left(c_1s_4\ -\ c_4s_1c_{23}\right)\right)\ -\ s_6\left(c_1c_4\ +\ s_4s_1c_{23}\right)\ \\ n_z&=c_6\left(s_5c_{23}+c_4c_5s_{23}\right)-s_4s_6s_{23}\\ o_x&=s_6\left(s_5c_1s_{23}-c_5\left(s_1s_4+c_4c_1c_{23}\right)\right)+c_6\left(c_4s_1-s_4c_1c_{23}\right)\\ o_y&=s_6\left(s_5s_1s_{23}+c_5\left(c_1s_4-c_4s_1c_{23}\right)\right)-c_6\left(c_1c_4+s_4s_1c_{23}\right)\\ o_z&=-s_6\left(s_5c_{23}\ +\ c_4c_5s_{23}\right)\ -\ c_6s_4s_{23}\\ a_x&=c_5c_1s_{23}+s_5\left(s_1s_4+c_4c_1c_{23}\right)\\ a_y&=c_5s_1s_{23}-s_5\left(c_1s_4-c_4s_1c_{23}\right)\\ a_z&=c_4s_5s_{23}-c_5c_{23}\\ p_x&=a_1c_1+a_3c_1c_{23}+d_4c_1s_{23}+a_2c_1c_2\\ p_y&=a_1s_1+a_3s_1c_{23}+d_4s_1s_{23}+a_2c_2s_1\\ p_z&=d_1+a_2s_2+a_3s_{23}-d_4c_{23} \end{aligned} nxnynzoxoyozaxayazpxpypz=s6(c4s1−s4c1c23)−c6(s5c1s23−c5(s1s4+c4c1c23)) =−c6(s5s1s23 + c5(c1s4 − c4s1c23)) − s6(c1c4 + s4s1c23) =c6(s5c23+c4c5s23)−s4s6s23=s6(s5c1s23−c5(s1s4+c4c1c23))+c6(c4s1−s4c1c23)=s6(s5s1s23+c5(c1s4−c4s1c23))−c6(c1c4+s4s1c23)=−s6(s5c23 + c4c5s23) − c6s4s23=c5c1s23+s5(s1s4+c4c1c23)=c5s1s23−s5(c1s4−c4s1c23)=c4s5s23−c5c23=a1c1+a3c1c23+d4c1s23+a2c1c2=a1s1+a3s1c23+d4s1s23+a2c2s1=d1+a2s2+a3s23−d4c23
matlab代码%连杆间齐次变换矩阵相乘得到机器人齐次变换矩阵T_0t=T_01*T_12*T_23*T_34*T_45*T_56;nx=T_0t(1,1);ny=T_0t(2,1);nz=T_0t(3,1);ox=T_0t(1,2);oy=T_0t(2,2);oz=T_0t(3,2);ax=T_0t(1,3);ay=T_0t(2,3);az=T_0t(3,3);px=T_0t(1,4);py=T_0t(2,4);pz=T_0t(3,4);△ 正运动学验证
这里用机器人工具箱的正解函数来验证机器人正运动学的位姿描述矩阵。将相同的关节角同时带入位姿描述矩阵与机器人工具箱,代码如下
clcclear all;%这里的输入为角度theta1=10;theta2=10;theta3=10;theta4=10;theta5=10;theta6=10;d1=1050;a1=500;a2=1300;a3=150;d4=1200;dt=390;%将角度转化为弧度Q1=theta1/180*pi;Q2=theta2/180*pi+pi/2;Q3=theta3/180*pi;Q4=theta4/180*pi;Q5=theta5/180*pi;Q6=theta6/180*pi;%ZK-500连杆间齐次变换矩阵T_01 =[ cos(Q1), -sin(Q1), 0, 0 sin(Q1), cos(Q1), 0, 0 0, 0, 1, d1 0, 0, 0, 1];T_12 =[ cos(Q2), -sin(Q2), 0, a1 0, 0, -1, 0 sin(Q2), cos(Q2), 0, 0 0, 0, 0, 1];T_23 =[ cos(Q3), -sin(Q3), 0, a2 sin(Q3), cos(Q3), 0, 0 0, 0, 1, 0 0, 0, 0, 1];T_34 =[ cos(Q4), -sin(Q4), 0, a3 0, 0, -1, -d4 sin(Q4), cos(Q4), 0, 0 0, 0, 0, 1];T_45 =[ cos(Q5), -sin(Q5), 0, 0 0, 0, 1, 0 -sin(Q5), -cos(Q5), 0, 0 0, 0, 0, 1];T_56 =[ cos(Q6), -sin(Q6), 0, 0 0, 0, -1, 0 sin(Q6), cos(Q6), 0, 0 0, 0, 0, 1];T_6t=[ 1 0 0 0 0 1 0 0 0 0 1 dt 0 0 0 1];%连杆间齐次变换矩阵相乘得到机器人齐次变换矩阵T_06=T_01*T_12*T_23*T_34*T_45*T_56;nx=T_06(1,1);ny=T_06(2,1);nz=T_06(3,1);ox=T_06(1,2);oy=T_06(2,2);oz=T_06(3,2);ax=T_06(1,3);ay=T_06(2,3);az=T_06(3,3);px=T_06(1,4);py=T_06(2,4);pz=T_06(3,4);%----------%机器人工具箱建立机器人模型% theta(z) d(z) a(x) alpha(x) L1=Link([ 0 d1 0 0 ],'modified');L2=Link([ 0 0 a1 pi/2 ],'modified');%将关节2的角度在初始值处补偿%L2.offset=pi/2;L3=Link([ 0 0 a2 0 ],'modified');L4=Link([ 0 d4 a3 pi/2 ],'modified');L5=Link([ 0 0 0 -pi/2 ],'modified');L6=Link([ 0 0 0 pi/2 ],'modified');Robot_6=SerialLink([L1,L2,L3,L4,L5,L6],'name','ZK-500');%----------%同时输出结果disp('齐次变换矩阵正解:');T_06disp('机器人工具箱正解:');Robot_6.fkine([Q1 Q2 Q3 Q4 Q5 Q6])注意这里轴2的转角 Q 2 Q_2 Q2要注意与轴1转角之间有90°的补偿量,需要在带入变换矩阵前添加进来,且在机器人工具箱中将补偿量去掉。
结果如下:

结果是一样的,但是变换矩阵的结果前面成了个1.0e+03的系数,怎么能把这个去掉呢。。。。【 ?】
好吧,正运动学就到这里。
❤ 2023.6.19 ❤
机器人逆运动学
CSDN提示我字数太多,一篇发不下,只好拆开,逆运动学的内容见
→→→【工业机器人运动学与Matlab正逆解算法学习笔记(用心总结一文全会)(二)——逆运动学P1】
→→→【工业机器人运动学与Matlab正逆解算法学习笔记(用心总结一文全会)(三)——逆运动学P2】
机器人雅可比矩阵
关于机器人雅可比矩阵的内容见
→→→【工业机器人运动学与Matlab正逆解算法学习笔记(用心总结一文全会)(四)——雅可比矩阵】