> 作者:დ旧言~
> 座右铭:松树千年终是朽,槿花一日自为荣。> 目标:手撕哈希表的闭散列和开散列
> 毒鸡汤: 坚持不懈,才能在困难面前看到光明的希望。
> 专栏选自:C嘎嘎进阶
> 望小伙伴们点赞👍收藏✨加关注哟💕💕

🌟前言
前面我们已经学习了开散列实现unordered_map与unordered_set的封装,在这个封装当中能拓展出一个知识点--->位图,位图其实是开散列实现unordered_map与unordered_set的封装的一个应用场景,那它这个实际应用到底是个啥呢?今天我们就来看看
⭐主体
学习位图咱们按照下面的图解:
🌙 位图的介绍
💫 位图的概念
概念分析:
位图就是bitmap的缩写,所谓bitmap,就是用每一位来存放某种状态,适用于大规模数据,该数据都是不重复的简单数据。通常是用来判断某个数据存不存在的
举个栗子:
案例:
给40亿个不重复的unsigned int的整数,没排过序的,然后再给一个数,如何快速判断这个数是否在那40亿个数当中?
分析:
如果不看数据量,我们第一想到的肯定就是依次从头遍历,但是这个数据量是非常大的,有40亿,遍历40亿次消耗的时间和内存是非常多的。但是引入位图后,就可以专门解决这种大量数据查找是否存在的问题。查找这个数是否存在所消耗的时间复杂度为O(1),且节省了32倍的容量(下面有解释)。
💫 位图的原理
问题抛出:
查找一个数是否存在,其实答案就是存在或者不存在,这种只需要回答是与否的问题,我们都可以用二进制中的位来表示,1表示该数存在,反之0表示该数不存在。而位图中的每个数据单元都是一个bit位,这样子平时我们都要话32位4字节来存储数据,而现在我们只需要花1个字节就能“存储数据”,在空间上减少了约32倍的容量。例如40G的数据我们只要花1.3G来存储。但是我们平时操作的数据类型最小就是一个字节,我们不能直接对位进行操作,所以我们可以借助位运算来对数据进行操作。
图解:
我们这里给出一个数组
int arr[] = {1,2,4,5,7,10,11,14,16,17,21,23,24,28,29,31};则我们只需要花1个字节来存这些数据

分析:
我们目前很多的机器都是小端存储,也就是低地址存低位,一个整形数据中,第一个字节用来存储0-7的数字,第二个字节用来存储8-15的数字,第三个字节用来存储16-23的数字,第四个字节用来存储24-31的数字。我们来看看数字10是如何存储的。先通过模上32,取余还是10,然后再将4字节中第10个比特位置为1,则表示该数字出现过。由于我们的机器是小端存储,所以我们的每个比特位都是要从右边开始计算的

总结:
所以说我们只需要将对应的比特位置为1即可。但是如果我们要存储的数据很大呢?其实也很简单,我们可以定义一个数组,当做一个位图,如果该数字在0-31之间,我们就存储在0号下标的元素中进行操作,如果在32-63之间,则就在1号下标之间进行操作。计算下标我们可以通过模32来获得下标。
💫 位图的应用
快速查找某个数据是否在一个集合中 排序 + 去重 求两个集合的交集、并集等 操作系统中磁盘块标记🌙 位图的使用
💫 位图的定义
方式一: 构造一个8位的位图,所有位默认初始化为0.
bitset<8> bs; //00000000方式二: 构造一个8位的位图,使用string类型对象初始化.
bitset<8> bs( string("1111" )) // 00001111方式三: 构造一个8位的位图,使用字符串"1111"初始化.
bit<8> bs("1111"); //00001111💫 位图的成员函数
相关函数:
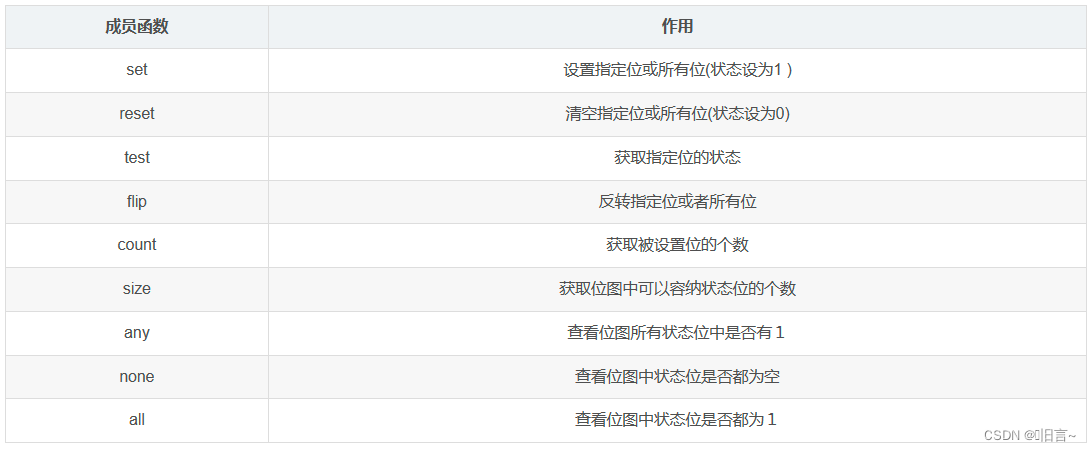
举个栗子:
int main(){bitset<8> bs("1110"); bs.set(0); //设置指定位cout << bs << endl; //00001111bs.reset(0); //清空指定位cout << bs << endl; //00001110bs.flip(0); //反转指定位cout << bs << endl; //00001111cout << bs.none() << endl; //0 cout << bs.any() << endl; //1bs.set(); //将位图所有位设置为1cout << bs.all() << endl; //1}注意事项:
set 和 reset 都是尾开始改变定位
💫 位图运算符的使用
举个栗子:
#include <bitset>#include <iostream>using namespace std;int main(){ bitset<8> bs; //00000000 //输入运算符 cin >> bs; //1111 //输出运算符 cout << bs << endl; //00001111 bitset<8> bs1("1110"); bitset<8> bs2("1100"); //位运算符 cout << (bs1 & bs2) << endl; // 0000 1100 cout << (bs1 | bs2) << endl; // 0000 1110 cout << (bs1 ^ bs2 ) << endl; // 0000 0010 //[]运算符 bs1[0] = 1; cout << bs1 << endl; //0000 1111; return 0;}🌙 位图的模拟实现
💫1.构造函数
分析:
在实现位图中,我们的成员变量只需要一个数组就可以实现。而这个数组有多我们要开多大呢?数组多开一个整形空间,就能多存32个数字,所以我们可以让用户提供一个准确的数,这个数是一个数据量,也是数的最大范围。我们可以通过该数模上32,就可以获得该数组的大小,但是0~31模上32为0,我们开0个空间那显然不合适,所以我们要开range/32 + 1个空间大小的数组
代码:
// 构造函数bitset() {_bits.resize(N / 32 + 1, 0);}💫2.存储数据
分析:
存储一个数字num需要3个步骤,第一是需要计算出该值对应的数组下标。计算数组下标方式为idx=num / 32;第二步是计算num在对应整数的比特位的位置bitIdx=num%32;第三步是要将计算出来的bite位置为1。我们之前说过,要操作位,我们可以通过位运算来操作,可以先将1左移bitIdx位后再和整数进行或运算
代码:
// 把x映射的位标记成1 (存储数据)void set(size_t x){assert(x <= N);size_t i = x / 32;size_t j = x % 32;_bits[i] |= (1 << j);}举例:
例如假设bitIdx=5,数据为10010011
1.将1进行左移5位==>100000
2.将数据和第一步计算出来的结果进行或运算
10010011 | 100000 =10110011,此时我们就将指定位置置位1了
💫3.删除数据
分析:
删除数据:删除数据和存储数据操作一样,唯一的区别就是将对应的bit位置为0。我们可以通过先将1进行左移bitIdx位,然后取反,将结果再和原来数据进行与运算
代码:
// 把x映射的位标记成1 (删除数据)void reset(size_t x){assert(x <= N);size_t i = x / 32;size_t j = x % 32;_bits[i] &= ~(1 << j);}举例:
例如假设bitIdx=5,数据为10110011
1.将1进行左移5位后并取反011111
2.将第一步计算出来的结果和数据进行与运算
10110011 & 011111 = 10010011,删除成功
💫4.检测
分析:
test成员函数的作用是检测x映射的状态位的状态
如果第j位的状态为 0, 那么经过与运算的结果就为0,转换为bool就表示false.如果第j位的状态位 1, 那么经过与运算的结果为1,转换为bool表示true.代码:
// 检测bool test(size_t x){assert(x <= N);size_t i = x / 32;size_t j = x % 32;return _bits[i] & (1 << j);}💫 全部代码
#include <vector>#include <assert.h>#include <iostream>using namespace std;namespace lyk{template<size_t N>class bitset{public:// 构造函数bitset() {_bits.resize(N / 32 + 1, 0);}// 把x映射的位标记成1 (存储数据)void set(size_t x){assert(x <= N);size_t i = x / 32;size_t j = x % 32;_bits[i] |= (1 << j);}// 把x映射的位标记成1 (删除数据)void reset(size_t x){assert(x <= N);size_t i = x / 32;size_t j = x % 32;_bits[i] &= ~(1 << j);}// 检测bool test(size_t x){assert(x <= N);size_t i = x / 32;size_t j = x % 32;return _bits[i] & (1 << j);}private:vector<int> _bits;};// 测试void test_bitset1(){bitset<100> bs1;bs1.set(50);bs1.set(30);bs1.set(90);for (size_t i = 0; i < 100; i++){if (bs1.test(i)){cout << i << "->" << "在" << endl;}else{cout << i << "->" << "不在" << endl;}}bs1.reset(90);bs1.set(91);cout << endl << endl;for (size_t i = 0; i < 100; i++){if (bs1.test(i)){cout << i << "->" << "在" << endl;}else{cout << i << "->" << "不在" << endl;}}bitset<-1> bs2;bitset<UINT_MAX> bs3;bitset<0xffffffff> bs4;}}🌙 位图应用场景
题目:
给定100亿个整数,设计算法找到只出现一次的整数?
分析:
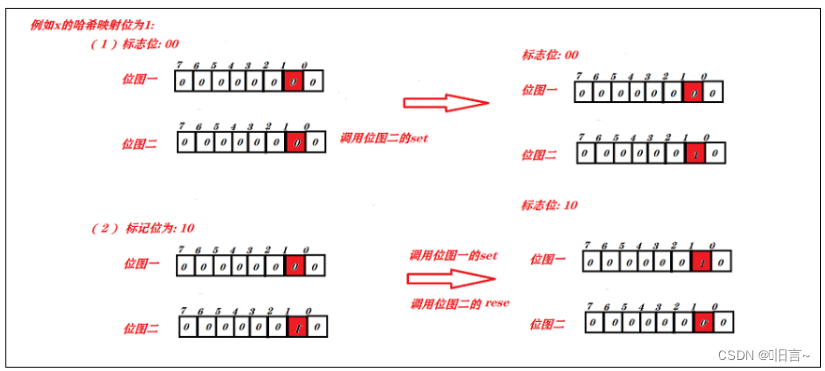
我们知道1个位图可以表示两种状态,那么两个位图可以表示四种状态,针对该题,我们可以设计以下三种状态: 00 出现零次 ,01 出现一次,10出现两次
步骤:
如果x映射位置的状态位为00, 则调用位图2的set,进而实现状态位为01.如果x映射位置的状态位为01,则调用位图1的set,位图2的reset,进而实现总状态位为10.图解:
代码:
template < size_t N >class twobit_set{public:void set(size_t x) {bool inset1 = _bs1.test(x);bool inset2 = _bs2.test(x);if ( inset1 == false && inset2 == false ) //如果状态为 00{_bs2.set(x); //设计为01;}else if (inset1 == false && inset2 == true) //如果状态为 01{_bs1.set(x); _bs2.reset(x); //设计为10}}void print_once_num() //遍历比特位,将数据在位图的状态位为01的数据打印.{for ( size_t i = 0; i < N; ++i ){if (_bs1.test(i) == false && _bs2.test(i) == true){cout << i << " ";}} }private:bit_set<N> _bs1;bit_set<N> _bs2;};🌟结束语
今天内容就到这里啦,时间过得很快,大家沉下心来好好学习,会有一定的收获的,大家多多坚持,嘻嘻,成功路上注定孤独,因为坚持的人不多。那请大家举起自己的小手给博主一键三连,有你们的支持是我最大的动力💞💞💞,回见。