MATLAB 之 绘制三维图形的基本函数、三维曲面和其他三维图形

点击全文阅读

文章目录

一、绘制三维曲线的基本函数二、三维曲面1. 平面网格坐标矩阵的生成2. 绘制三维曲面的函数3. 标准三维曲面 三、其他三维图形1. 三维条形图2. 三维饼图3. 三维实心图4. 三维散点图5. 三维杆图6. 三维箭头图

三维图形具有更强的数据表现能力，为此 MATLAB 提供了丰富的函数来绘制三维图形。绘制三维图形与绘制二维图形的方法十分类似，很多都是在二维绘图的基础上扩展而来。

一、绘制三维曲线的基本函数

基本的三维图形函数为 plot3，它是将二维绘图函数 plot 的有关功能扩展到三维空间，用来绘制三维曲线。plot3 函数与 plot 函数用法十分相似，其调用格式如下：

plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n) 

其中，每一组 x 、 y 、 z x、y、z x、y、z 组成一组曲线的坐标参数，选项的定义和 plot 函数相同（线型、颜色和标记符号等参数，详见 MATLAB 之 二维图形绘制的基本函数和辅助操作）。当 x 、 y 、 z x、y、z x、y、z 是同长度的向量时，则 x 、 y 、 z x、y、z x、y、z 对应元素构成一条三维曲线。当 x 、 y 、 z x、y、z x、y、z 是同型矩阵时，则以 x 、 y 、 z x、y、z x、y、z 对应列元素绘制三维曲线，曲线条数等于矩阵列数。例如，我们绘制空间曲线： { x 2 + y 2 + z 2 = 64 y + z = 0 \left\{\begin{matrix}x^{2}+y^{2}+z^{2}=64 \\y+z=0 \end{matrix}\right. {x2+y2+z2=64y+z=0​曲线对应的参数方程为 { x = 8 cos ⁡ t y = 4 2 sin ⁡ t z = − 4 2 sin ⁡ t , 0 ≤ t ≤ 2 π \left\{\begin{matrix}x=8\cos t \\y=4\sqrt{2} \sin t \\z=-4\sqrt{2} \sin t \end{matrix}\right.\begin{matrix},0\le t\le 2\pi \end{matrix} ⎩ ⎨ ⎧​x=8costy=42 ​sintz=−42 ​sint​,0≤t≤2π​程序如下：

t=0:pi/50:2*pi;x=8*cos(t);y=4*sqrt(2)*sin(t);z=-4*sqrt(2)*sin(t);plot3(x,y,z,'p');title('Line in 3-D Space');text(0,0,0,'origin');axis ([-10,10,-10,10,-6,6]);xlabel('X');ylabel('Y');zlabel('Z');grid;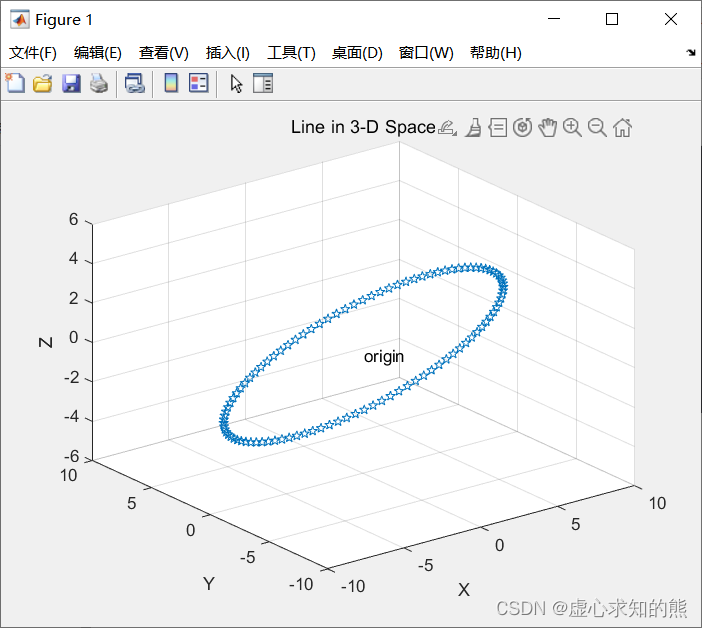

程序运行结果如下图所示。

二、三维曲面

1. 平面网格坐标矩阵的生成

绘制 z = f ( x , y ) z=f(x,y) z=f(x,y) 所代表的三维曲面图，先要在 x y xy xy 平面选定一矩阵区域，假定矩形区域 D = [ a , b ] × [ c , d ] D=[a,b]×[c,d] D=[a,b]×[c,d]，然后将 [ a , b ] [a,b] [a,b] 在 x x x 方向分成 m m m 份，将 [ c , d ] [c,d] [c,d] 在 y y y 方向分成 n n n 份。由各划分点分别作平行于两坐标轴的直线，将区域 D D D 分成 m × n m×n m×n 个小矩形，生成代表每一个小矩形顶点坐标的平面网格坐标矩阵，最后利用有关函数进行绘图即可。产生平面区域内的网格坐标矩阵有以下两种方法。（1） 利用矩阵运算生成。

x=a:dx:b;y=(c:dy:d)';X=ones(size(y))*x;Y=y*ones(size(x));

在上述程序段中，矩阵 X 的 X的 X的 每一行都是向量 x x x， 行数等于向量 y y y 的元素的个数，矩阵 Y Y Y 的每一列都是向量 y y y，列数等于向量 x x x 的元素的个数。于是 X X X 和 Y Y Y相同位置上的元素 ( X ( i , j ) ， Y ( i , j ) (X(i, j)，Y(i, j) (X(i,j)，Y(i,j) 恰好是区域 D D D 的 ( i , j ) (i, j) (i,j) 网格点的坐标。若根据每一个网格点上的 x 、 y x、y x、y坐标求函数值 z z z，则得到函数值矩阵 Z Z Z。显然， X 、 Y 、 Z X、Y、Z X、Y、Z 各列或各行所对应坐标，对应于一条空间曲线，空间曲线的集合组成空间曲面。（2） 利用 meshgrid 函数生成。

x=a:dx:b;y=c:dy:d;[X,Y]=meshgrid(x,y);

程序段运行后，所得到的网格坐标矩阵 X 、 Y X、Y X、Y与方法（1）得到的相同。当 x = y x=y x=y 时，meshgrid 函数可写成 meshgrid(x)。为了说明网格坐标矩阵的用法，下面举一个例子， 该例子巧妙地利用网格坐标矩阵来解不定方程。例如，已知 6 < x < 30 ， 15 < y < 36 6<x<30，15<y<36 6<x<30，15<y<36，我们求不定方程 2 x + 5 y = 126 2x+5y=126 2x+5y=126 的整数解。程序如下：

x=7:29;y=16:35;[x,y]=meshgrid(x,y);  %在[7,29]*[16,35]区域生成网格坐标z=2*x+5*y;k=find(z==126);  %找出解的位置x(k)'  %输出对应位置的x即方程的解y(k)'  %输出对应位置的y即方程的解

程序运行结果如下：

ans =     8    13    18    23ans =    22    20    18    16

即方程总共有 4 组解：(8,22)、(13,20)、(18,18)、(23,16)。

2. 绘制三维曲面的函数

MATLAB 提供了 mesh 函数和 surf 函数来绘制三维曲面图。mesh 函数用于绘制三维网格图。在不需要绘制特别精细的三维曲面图时，可以通过三维网格图来表示三维曲面。surf 函数用于绘制三维曲面图，各线条之间的补面用颜色填充。mesh 函数和 surf 函数的调用格式如下：

mesh(x,y,z,c)surf(x,y,z,c)

一般情况下， x 、 y 、 z x、y、z x、y、z 是同型矩阵。 x 、 y x、y x、y 是网格坐标矩阵， z z z 是网格点上的高度矩阵， c c c 称为色标（color scale）矩阵，用于指定曲面的颜色。在默认情况下，系统根据 c c c 中元素大小的比例关系，把色标数据变换成色图矩阵中对应的颜色。当 c c c 省略时，MATLAB 认为 c = z c=z c=z，亦即颜色的设定正比于图形的高度，这样就可以得出层次分明的三维图形。当 x 、 y x、y x、y 省略时，把 z z z 矩阵的列下标当作 x x x 轴坐标，把 z z z 矩阵的行下标当作 y y y 轴坐标，然后绘制三维曲面图。当 x 、 y x、y x、y 是向量时，要求 x x x 的长度等于 z z z 矩阵的列数， y y y 的长度等于 z z z 矩阵的行数， x 、 y x、y x、y 向量元素的组合构成网格点的 x 、 y x、y x、y 坐标， z z z 坐标则取自 z z z 矩阵，然后绘制三维曲面图。例如，我们绘制三维曲面图 z = sin ⁡ y cos ⁡ x z=\sin y\cos x z=sinycosx。为便于分析各种三维曲面的特征，下面画出了 3 种不同形式的曲面。程序 1 如下：

x=0:0.1:2*pi;[x,y]=meshgrid(x);z=sin(y).*cos(x);mesh(x,y,z);xlabel('x-axis');ylabel('y-axis');zlabel('z-axis');title('mesh');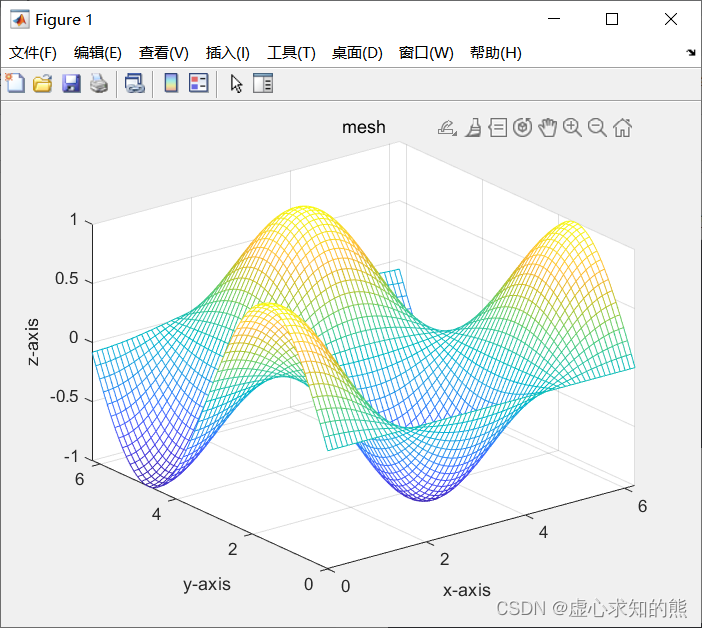

程序 1 运行结果如下图所示。

程序 2 如下：

x=0:0.1:2*pi;[x,y]=meshgrid(x);z=sin(y).*cos(x);surf(x,y,z);xlabel('x-axis');ylabel('y-axis');zlabel('z-axis');title('surf');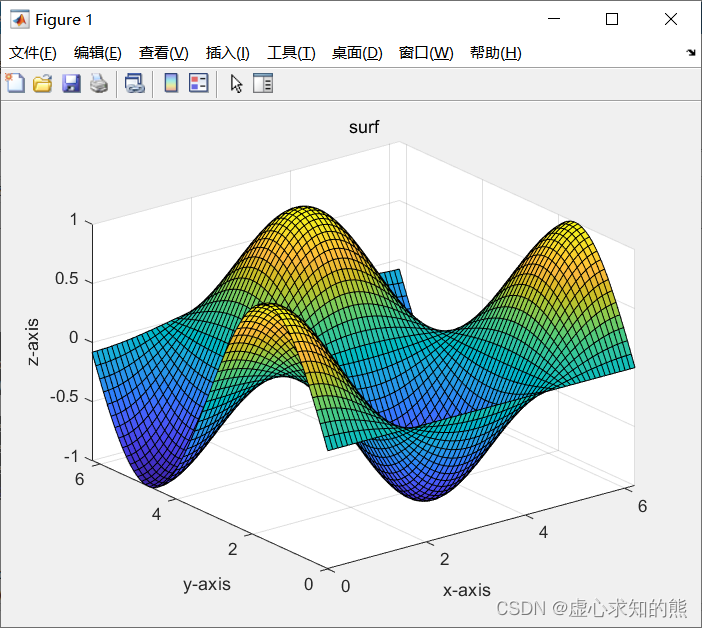

程序 2 运行结果如下图所示。

程序 3 如下：

x=0:0.1:2*pi;[x, y]=meshgrid(x);z=sin(y).*cos(x);plot3(x,y,z);xlabel('x-axis');ylabel('y-axis');zlabel('z-axis');title('plot3');grid;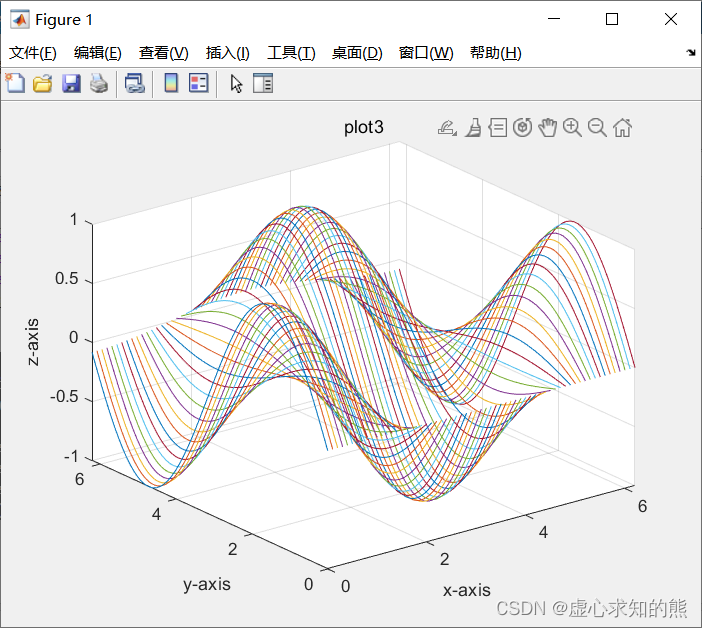

程序 3 运行结果如下图所示。

网格图（mesh）中线条有颜色，线条间补面无颜色。曲面图（surf）的线条是黑色，线条间补面有颜色。曲面图补面颜色和网格图线条颜色都是沿 z z z 轴变化的。用 plot3 绘制的三维曲面实际上由三维曲线组合而成。例如，我们绘制两个相互垂直且直径相等相等的圆柱体的相交图形。程序如下：

m=30;z=1.2*(0:m)/m; r=ones(size(z));theta=(0:m)/m*2*pi;x1=r'*cos(theta);  %生成第一个圆柱体的坐标矩阵y1=r'*sin(theta);z1=z'*ones(1,m+1);x=(-m:2:m)/m;x2=x'*ones(1,m+1);  %生成第二个圆柱体的坐标矩阵y2=r'*cos(theta);z2=r'*sin(theta);surf(x1,y1,z1);  %绘制垂直的圆柱体axis equal;axis off;hold on;surf(x2,y2,z2);  %绘制水平的圆柱体axis equal;axis off;title('两个圆柱体的相交图形');hold off;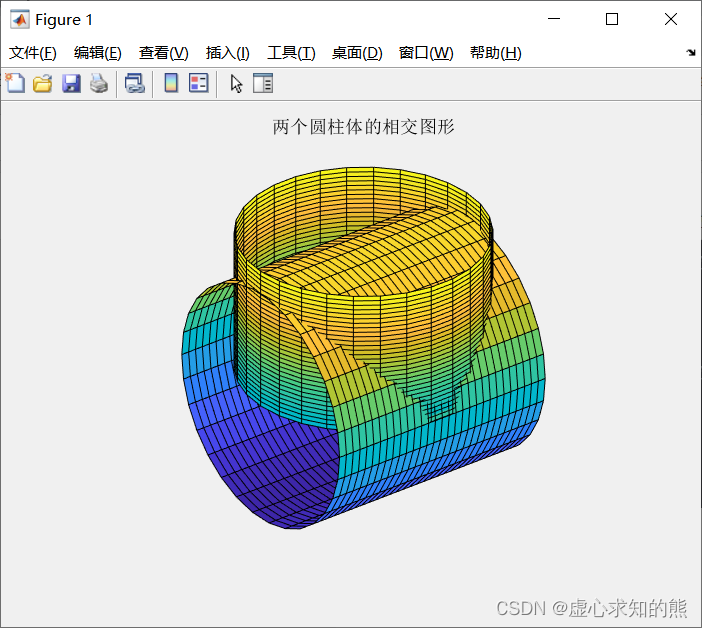

程序运行结果如下图所示。

例如，我们分析 z = x 2 − 2 y 2 z=x^{2} -2y^{2} z=x2−2y2 构成的曲面形状及与平面 z = a z=a z=a 的交线。程序如下：

[x,y]=meshgrid(-10:0.2:10);z1=(x.^2-2*y.^2)+eps;  %第一个曲面坐标a=input('a= ');z2=a*ones(size(x));  %第二个曲面坐标subplot(1,2,1);mesh(x,y,z1);hold on;mesh(x,y,z2);  %分别画出两个曲面v=[-10,10,-10,10,-100,100];  %第一子图的坐标设置axis(v);grid;hold off;r0=abs(z1-z2)<=1;  %求两曲面z坐标差小于1的点xx=r0.*x;yy=r0.*y;zz=r0.*z2;  %求这些点上的x、y、z坐标，即交线坐标subplot(1,2,2);plot3(xx(r0~=0),yy(r0~=0),zz(r0~=0),'*');  %在第二子图画出交线axis(v);  %第二子图的坐标设置grid;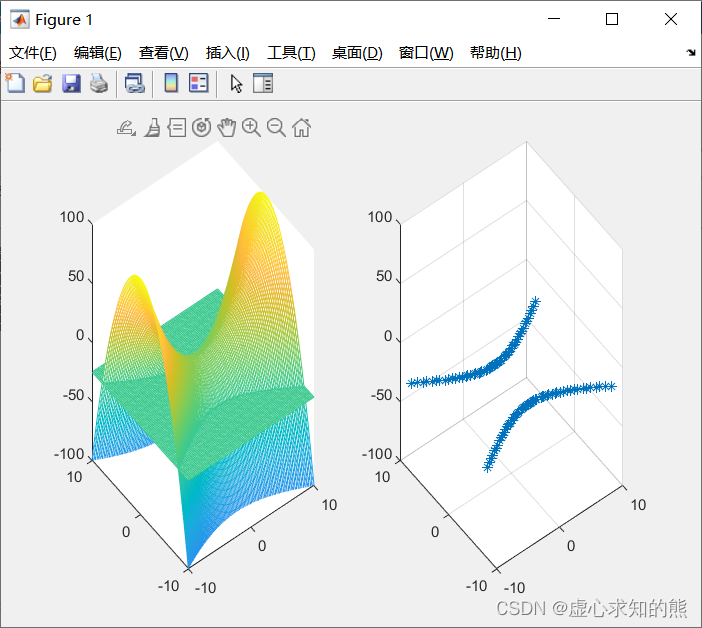

程序运行时，如果我们输入 a = − 25 a=-25 a=−25，所得三维曲面图和曲面的交线如下图所示。当我们输入的 a a a 不同时，曲面的交线就会发生变化。

此外，还有两个和 mesh 函数相似的函数，即带等高线的三维网格曲面函数 meshc 和带底座的三维网格曲面函数 meshz。其用法与 mesh 类似，不同的是 meshe 还在 x y xy xy 平面上绘制曲面在 z z z 轴方向的等高线，meshz 还在 x y xy xy 平面上绘制曲面的底座。函数 surf 也有两个类似的函数，即具有等高线的曲面函数 surfc 和具有光照效果的曲面函数 surfl。例如，在 x y xy xy 平面内选择区域 [ − 8 , 8 ] × [ − 8 , 8 ] [-8,8]×[-8,8] [−8,8]×[−8,8] ，我们绘制函数 z = sin ⁡ x 2 + y 2 x 2 + y 2 z=\frac{\sin \sqrt{x^{2} +y^{2} } }{\sqrt{x^{2} +y^{2}}} z=x2+y2 ​sinx2+y2 ​​ 的 4 种三维曲面图（墨西哥帽子图形）。程序如下：

[x,y]=meshgrid(-8:0.5:8);z=sin(sqrt(x.^2+y.^2))./sqrt(x.^2+y.^2+eps);subplot(2,2,1);meshc(x,y,z) ;title('meshc(x,y,z)');subplot(2,2,2);meshz(x,y,z);title('meshz(x,y,z)');subplot(2,2,3);surfc(x,y,z);title('surfc(x,y,z)');subplot(2,2,4);surfl(x,y,z);title('surfl(x,y,z)');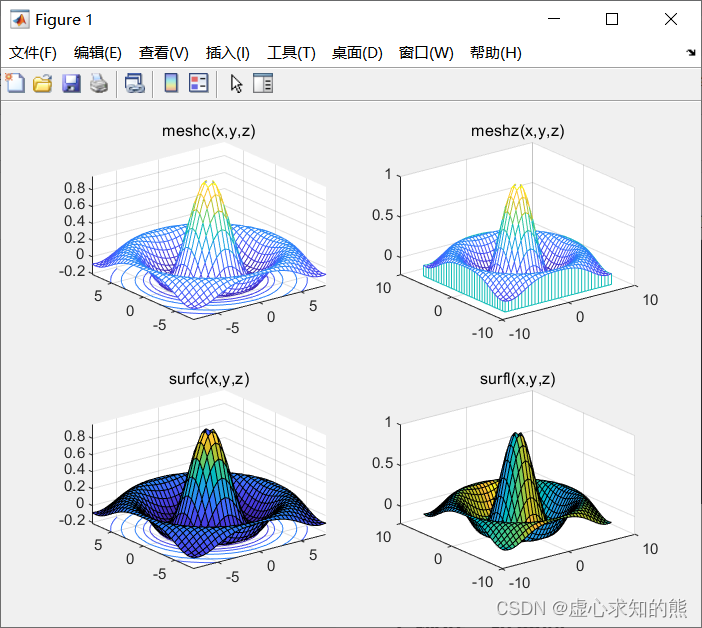

程序运行结果如下图所示。

3. 标准三维曲面

MATLAB 提供了一些的数用 于绘制标准三维曲面，还可以利用这些的数产生相应的绘图数据，常用于三维图形的演示。例如，sphere 函数和 cylinder 函数分别用于绘制三维球面和柱面。sphere 函数的调用格式如下：

    [x,y,z]=sphere(n)

该函数将产生 ( n + 1 ) × ( n + 1 ) (n+1)×(n+1) (n+1)×(n+1) 矩阵 x 、 y 、 z x、 y、z x、y、z，采用这 3 个矩阵可以绘制出圆心位于原点、半径为 1 的单位球体。若在调用该函数时不带输出参数，则直接绘制所需球面。 n n n 决定了球面的圆滑程度，其默认值为 20。若 n n n 值取得较小，则将绘制出多面体表面图。cylinder 函数的调用格式如下：

    [x,y,z]=cylinder(R,n)

其中， R R R 是一个向量，存放柱面各个等间隔高度上的半径， n n n 表示在圆柱圆周上有 n n n 个间隔点，默认有 20 个间隔点。例如：

>> cylinder(3)

将生成一个圆柱。又例如：

>> cylinder([10,0])

将生成一个圆锥，而执行下列命令：

>> t=0:pi/100:4*pi;>> R=sin(t);>> cylinder(R,30);

将生成一个正弦型柱面。另外，生成矩阵的大小与 R R R 向量的长度及 n n n 有关。其余用法与 sphere 函数相同。MATLAB 还有一个 peaks 函数，称为多峰函数，常用于三维曲面的演示。该函数可以用来生成绘图数据矩阵，矩阵元素由以下函数在矩形区域 [ − 3 , 3 ] × [ − 3 , 3 ] [-3,3]×[-3,3] [−3,3]×[−3,3] 的等分网格点上的函数值确定。 f ( x , y ) = 3 ( 1 − x 2 ) e − x 2 − ( y + 1 ) 2 − 10 ( x 5 − x 3 − y 5 ) e − x 2 − y 2 − 1 3 e − ( x + 1 ) 2 − y 2 f(x,y)=3(1-x^{2})e^{-x^{2}-(y+1)^{2}}-10(\frac{x}{5}-x^{3}-y^{5})e^{-x^{2}-y^{2}}-\frac{1}{3}e^{-(x+1)^{2}-y^{2}} f(x,y)=3(1−x2)e−x2−(y+1)2−10(5x​−x3−y5)e−x2−y2−31​e−(x+1)2−y2例如：

    z=peaks(30);

将生成一个 30 × 30 30×30 30×30 的矩阵 z z z，即分别沿 x x x 和 y y y 方向将区间 [ − 3 , 3 ] [-3,3] [−3,3] 等分成 29 份，并计算这些网格点上的函数值。默认的等分数是 48，即 p=peaks 将生成一个 49 × 49 49×49 49×49 的矩阵 p p p。也可以根据网格坐标矩阵 x 、 y x、y x、y 重新计算函数矩阵。例如：

>> [x,y]=meshgrid(-5:0.1:5);>> z=peaks(x,y);

生成的数值矩阵可以作为 mesh、surf 等函数的参数而绘制出多峰函数曲面图。另外，若在调用 peaks 函数时不带输出参数，则直接绘制出多峰函数曲面图。例如，我们绘制标准三维曲面图形。程序如下：

t=0:pi/20:2*pi;[x,y,z]=cylinder(2+sin(t),30);subplot(1,3,1);surf(x,y,z);  %生成一个正弦型柱面axis([-5,5,-5,5,0,1]);[x,y,z]=sphere;subplot(1,3,2);surf(x,y,z);  %生成一个球面axis equal;[x,y,z]=peaks(30);subplot(1,3,3);meshz(x,y,z);  %生成一个多峰曲面axis([-5,5,-5,5,-10,10]);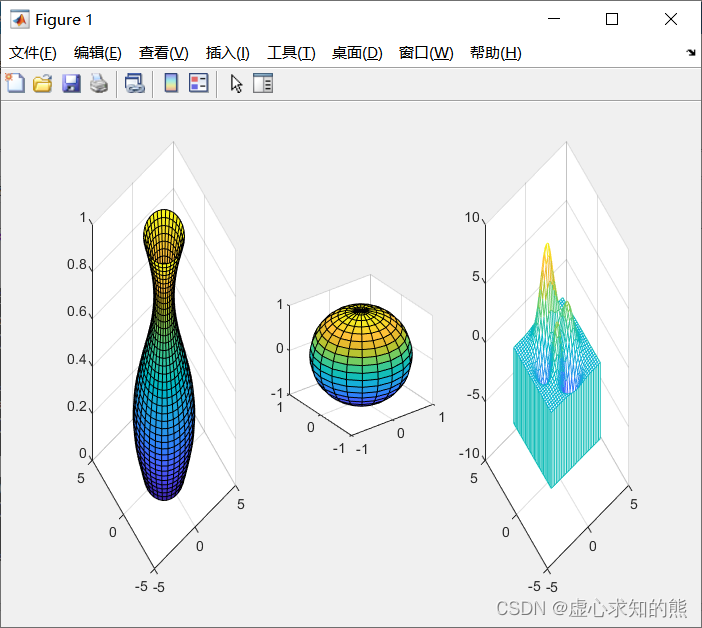

程序运行结果如下图所示。

三、其他三维图形

在介绍二维图形时，曾提到各种特殊图形，有些还可以以三维形式出现，使用的函数包括 bar3、bar3h、 pie3、 fill3、 scatter3、 stem3 和 quiver3。

1. 三维条形图

bar3 函数绘制三维条形图，常用格式如下：

    bar3 (y)    bar3(x,y)

在第一种格式中， y y y 的每个元素对应于一个条形。第二种格式在 x x x 指定的位置上绘制 y y y 中元素的条形图。bar3h 的用法与 bar3 相同。

2. 三维饼图

pie3 函数绘制三维饼图，常用格式如下：

    pie3(x,explode)

其中 x x x 为向量，用 x x x 中的数据绘制一个三维饼图，explode 设置相应的扇形是否偏离整体图形。

3. 三维实心图

fill3 函数可在三维饼图内绘制出填充过的多边形，常用格式如下：

    fill3(x,y,z,c)

其中使用 x 、 y 、 z x、y、z x、y、z 作为多边形的顶点，而 c c c 指定了填充的颜色。

4. 三维散点图

scatter3 函数可在三维空间内绘制散点图，常用格式如下：

    scatter3(x,y,z,c)

其中 x 、 y 、 z x、y、z x、y、z 必须时等长度的向量，而 c c c 指定了填充的颜色。

5. 三维杆图

stem3 函数绘制离散序列数据的三维杆图，常用格式如下：

    stem3(z)    stem3(x,y,z)

第一种将数据序列 z z z 表示为从 x y xy xy 平面向上延申的杆图， x x x 和 y y y 自动生成。第二种格式在 x x x 和 y y y 指定的位置上绘制数据序列 z z z 的杆图。

6. 三维箭头图

quiver3 函数绘制三维空间的矢量图，常用格式如下：

    quiver3(x,y,z,u,v,w)

其中 x 、 y 、 z 、 u 、 v 、 w x、y、z、u、v、w x、y、z、u、v、w 必须长度一样，绘制三维矢量图。矢量由 ( u , v , w ) (u,v,w) (u,v,w) 决定，所在位置由 ( x , y , z ) (x,y,z) (x,y,z) 决定。例如，quiver3(1,2,3,4,5,6) 是以 (1,2,3) 为起点绘制一个矢量，即一个由 (1,2,3) 指向 (4,5,6) 的箭头。例如，我们绘制以下三维图形。（1） 绘制魔方阵的三维条形图。（2） 已知 x = [ 2347 , 1827 , 2043 , 3025 ] x=[2347,1827,2043,3025] x=[2347,1827,2043,3025]，绘制三维饼图。（3） 用随机的顶点坐标值画出 5 个黄色三角形。（4） 以三位杆图形式绘制曲线 y = sin ⁡ x y=\sin x y=sinx。整体程序如下：

subplot(2,2,1);bar3(magic(4));title('（1）bar3');subplot(2,2,2);pie3([2347,1827,2043,3025]);title('（2）pie3');a=rand(3,5);b=rand(3,5);c=rand(3,5);subplot(2,2,3);fill3(a,b,c,'y');title('（3）fill3');y=2*sin(0:pi/10:2*pi);subplot(2,2,4);stem3(y);title('（4）stem3');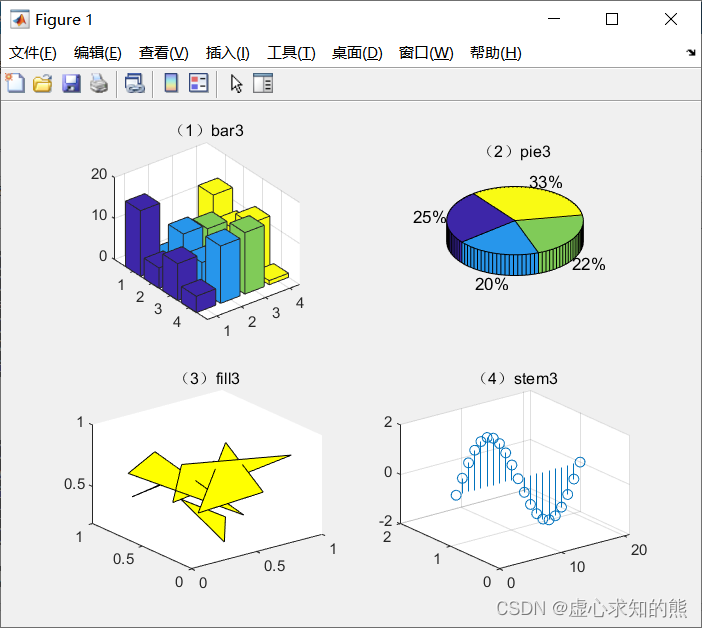

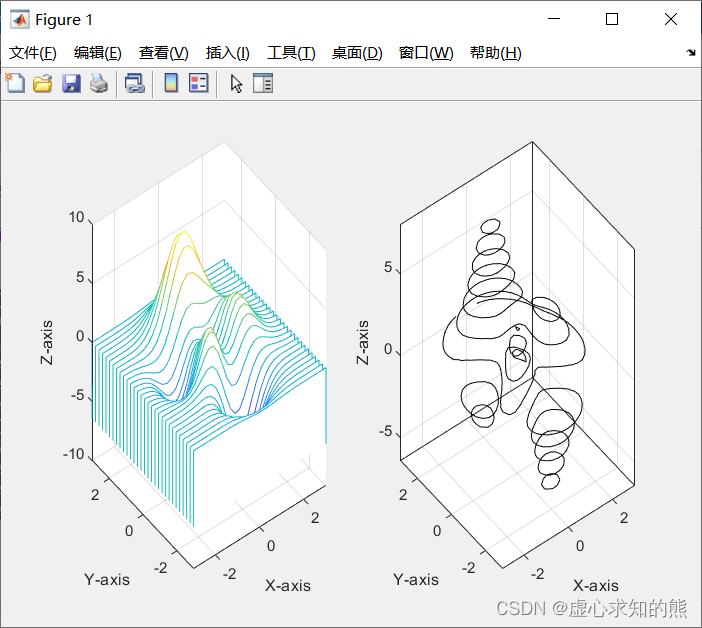
整体程序运行结果如下图所示。

除了上面讨论的三维图形外，常用图形还有瀑布图、三维曲面的等高线图。绘制瀑布图用 watrall 函数，它的用法及图形效果与 meshz 函数相似，只是它的网格线是在 x x x 轴方向出现，具有瀑布效果。等高线图分二维和三维两种形式，分别使用函数 contour 和 contour3 绘制。例如，我们绘制多峰函数的瀑布图和等高线图。程序如下：

subplot(1,2,1);[X,Y,Z]=peaks(30);waterfall(X,Y,Z)xlabel('X-axis');ylabel('Y-axis');zlabel('Z-axis');subplot(1,2,2);contour3(X,Y,Z,12,'k');  %其中12代表高度的等级数xlabel('X-axis');ylabel('Y-axis');zlabel('Z-axis');

程序运行结果如下图所示。

点击全文阅读