时间序列分析——基于R | 第3章 ARMA模型的性质
往期文章
时间序列分析——基于R | 第1章习题代码
时间序列分析——基于R | 第2章时间序列的预处理习题代码
已知某 A R ( 1 ) AR(1) AR(1)模型为: x t = 0.7 x t − 1 + ε t , ε t ∼ W N ( 0 , 1 ) . x_t=0.7x_{t-1}+\varepsilon_t,\varepsilon_t \sim WN(0,1). xt=0.7xt−1+εt,εt∼WN(0,1).求 E ( x t ) , V a r ( x t ) , ρ 2 E(x_t),Var(x_t),\rho_2 E(xt),Var(xt),ρ2和 ϕ 22 . \phi_{22}. ϕ22.
E ( x t ) = ϕ 0 1 − ϕ 1 = 0 1 − 0.7 = 0 E\left(x_t\right)=\frac{\phi_{0}}{1-\phi_{1}}=\frac{0}{1-0.7}=0 E(xt)=1−ϕ1ϕ0=1−0.70=0
V a r ( x t ) = 1 1 − ϕ 1 2 = 1 1 − 0. 7 2 = 1.96 Var(x_t)=\frac{1}{1-\phi_{1}^{2}}=\frac{1}{1-0.7^2}=1.96 Var(xt)=1−ϕ121=1−0.721=1.96
ρ 2 = ϕ 1 2 = 0. 7 2 = 0.49 \rho_2=\phi_1^2=0.7^2=0.49 ρ2=ϕ12=0.72=0.49
ϕ 22 = ∣ 1 ρ 1 ρ 1 ρ 2 ∣ ∣ 1 ρ 1 ρ 1 1 ∣ = 0.49 − 0. 7 2 1 − 0. 7 2 = 0 \phi_{22}=\frac{\left|\begin{array}{cc}1 & \rho_{1} \\\rho_{1} & \rho_{2}\end{array}\right|}{\left|\begin{array}{cc}1 & \rho_{1} \\\rho_{1} & 1\end{array}\right|}=\frac{0.49-0.7^{2}}{1-0.7^{2}}=0 ϕ22= 1ρ1ρ11 1ρ1ρ1ρ2 =1−0.720.49−0.72=0
已知某 AR ( 2 ) \operatorname{AR}(2) AR(2) 模型为: x t = ϕ 1 x t − 1 + ϕ 2 x t − 2 + ε t , ε t ∼ W N ( 0 , σ ε 2 ) x_t=\phi_1 x_{t-1}+\phi_2 x_{t-2}+\varepsilon_t, \varepsilon_t \sim W N\left(0, \sigma_{\varepsilon}^2\right) xt=ϕ1xt−1+ϕ2xt−2+εt,εt∼WN(0,σε2), 且 ρ 1 = \rho_1= ρ1= 0.5 , ρ 2 = 0.3 0.5, \rho_2=0.3 0.5,ρ2=0.3, 求 ϕ 1 , ϕ 2 \phi_1, \phi_2 ϕ1,ϕ2 的值.
A R ( 2 ) A R(2) AR(2) 模型有:
{ ρ 1 = ϕ 1 1 − ϕ 2 ρ 2 = ϕ 1 ρ 1 + ϕ 2 ⇒ { 0.5 = ϕ 1 1 − ϕ 2 0.3 = 0.5 ϕ 1 + ϕ 2 ⇒ { ϕ 1 = 7 15 , ϕ 2 = 1 15 ϕ 2 = 1 15 \left\{\begin{array} { l } { \rho _ { 1 } = \frac { \phi _ { 1 } } { 1 - \phi _ { 2 } } } \\ { \rho _ { 2 } = \phi _ { 1 } \rho _ { 1 } + \phi _ { 2 } } \end{array} \Rightarrow \left\{\begin{array} { l } { 0 . 5 = \frac { \phi _ { 1 } } { 1 - \phi _ { 2 } } } \\ { 0 . 3 = 0 . 5 \phi _ { 1 } + \phi _ { 2 } } \end{array} \Rightarrow \left\{\begin{array}{l} \phi_1=\frac{7}{15}, \phi_2=\frac{1}{15} \\ \phi_2=\frac{1}{15} \end{array}\right.\right.\right. {ρ1=1−ϕ2ϕ1ρ2=ϕ1ρ1+ϕ2⇒{0.5=1−ϕ2ϕ10.3=0.5ϕ1+ϕ2⇒{ϕ1=157,ϕ2=151ϕ2=151
已知某 AR ( 2 ) \operatorname{AR}(2) AR(2) 模型为: ( 1 − 0.5 B ) ( 1 − 0.3 B ) x t = ε t , ε t ∼ W N ( 0 , 1 ) (1-0.5 B)(1-0.3 B) x_t=\varepsilon_t, \varepsilon_t \sim W N(0,1) (1−0.5B)(1−0.3B)xt=εt,εt∼WN(0,1), 求 E ( x t ) E\left(x_t\right) E(xt), Var ( x t ) , ρ k , ϕ k k \operatorname{Var}\left(x_t\right), \rho_k, \phi_{k k} Var(xt),ρk,ϕkk, 其中 k = 1 , 2 , 3 k=1,2,3 k=1,2,3.
(1) ( 1 − 0.5 B ) ( 1 − 0.3 B ) x t = ε t ⇔ x t = 0.8 x t − 1 − 0.15 x t − 2 + ε t (1-0.5 B)(1-0.3 B) x_t=\varepsilon_t \Leftrightarrow x_t=0.8 x_{t-1}-0.15 x_{t-2}+\varepsilon_t (1−0.5B)(1−0.3B)xt=εt⇔xt=0.8xt−1−0.15xt−2+εt
E ( x t ) = ϕ 0 1 − ϕ 1 − ϕ 2 = 0 E\left(x_t\right)=\frac{\phi_0}{1-\phi_1-\phi_2}=0 E(xt)=1−ϕ1−ϕ2ϕ0=0
(2)
Var ( x t ) = 1 − ϕ 2 ( 1 + ϕ 2 ) ( 1 − ϕ 1 − ϕ 2 ) ( 1 + ϕ 1 − ϕ 2 ) = 1 + 0.15 ( 1 − 0.15 ) ( 1 − 0.8 + 0.15 ) ( 1 + 0.8 + 0.15 ) = 1.98 \begin{aligned} \operatorname{Var}\left(x_t\right) & =\frac{1-\phi_2}{\left(1+\phi_2\right)\left(1-\phi_1-\phi_2\right)\left(1+\phi_1-\phi_2\right)} \\ & =\frac{1+0.15}{(1-0.15)(1-0.8+0.15)(1+0.8+0.15)} \\ & =1.98 \end{aligned} Var(xt)=(1+ϕ2)(1−ϕ1−ϕ2)(1+ϕ1−ϕ2)1−ϕ2=(1−0.15)(1−0.8+0.15)(1+0.8+0.15)1+0.15=1.98
(3)
ρ 1 = ϕ 1 1 − ϕ 2 = 0.8 1 + 0.15 = 0.70 ρ 2 = ϕ 1 ρ 1 + ϕ 2 = 0.8 × 0.7 − 0.15 = 0.41 ρ 3 = ϕ 1 ρ 2 + ϕ 2 ρ 1 = 0.8 × 0.41 − 0.15 × 0.7 = 0.22 \begin{aligned} & \rho_1=\frac{\phi_1}{1-\phi_2}=\frac{0.8}{1+0.15}=0.70 \\ & \rho_2=\phi_1 \rho_1+\phi_2=0.8 \times 0.7-0.15=0.41 \\ & \rho_3=\phi_1 \rho_2+\phi_2 \rho_1=0.8 \times 0.41-0.15 \times 0.7=0.22 \end{aligned} ρ1=1−ϕ2ϕ1=1+0.150.8=0.70ρ2=ϕ1ρ1+ϕ2=0.8×0.7−0.15=0.41ρ3=ϕ1ρ2+ϕ2ρ1=0.8×0.41−0.15×0.7=0.22
(4)
ϕ 11 = ρ 1 = 0.7 ϕ 22 = ϕ 2 = − 0.15 ϕ 33 = 0 \begin{aligned} \phi_{11} & =\rho_1=0.7 \\ \phi_{22} & =\phi_2=-0.15 \\ \phi_{33} & =0 \end{aligned} ϕ11ϕ22ϕ33=ρ1=0.7=ϕ2=−0.15=0
已知 AR ( 2 ) \operatorname{AR}(2) AR(2) 序列为 x t = x t − 1 + c x t − 2 + ε t x_t=x_{t-1}+c x_{t-2}+\varepsilon_t xt=xt−1+cxt−2+εt, 其中 { ε t } \left\{\varepsilon_t\right\} {εt} 为白噪声序列. 确定 c c c 的取值范围, 以保证 { x t } \left\{x_t\right\} {xt} 为平稳序列, 并给出该序列 ρ k \rho_k ρk 的表达式.
(1) A R ( 2 ) A R(2) AR(2) 模型的平稳条件是
{ ∣ c ∣ < 1 c ± 1 < 1 ⇒ { − 1 < c < 1 c < 0 ⇒ − 1 < c < 0 \left\{\begin{array}{l}|c|<1 \\ c \pm 1<1\end{array} \Rightarrow\left\{\begin{array}{l}-1<c<1 \\ c<0\end{array} \Rightarrow-1<c<0\right.\right. {∣c∣<1c±1<1⇒{−1<c<1c<0⇒−1<c<0
(2) { ρ 1 = 1 1 − c , ρ k = ρ k − 1 + c ρ k − 2 , k ≥ 2 \left\{\begin{array}{l}\rho_{1}=\frac{1}{1-c}, \\ \rho_{k}=\rho_{k-1}+c \rho_{k-2}, k \geq 2\end{array}\right. {ρ1=1−c1,ρk=ρk−1+cρk−2,k≥2
证明对任意常数 c c c, 如下定义的 A R ( 3 ) \mathrm{AR}(3) AR(3) 序列一定是非平稳序列:
x t = x t − 1 + c x t − 2 − c x t − 3 + ε t , ε t ∼ W N ( 0 , σ ε 2 ) x_t=x_{t-1}+c x_{t-2}-c x_{t-3}+\varepsilon_t, \varepsilon_t \sim W N\left(0, \sigma_{\varepsilon}^2\right) xt=xt−1+cxt−2−cxt−3+εt,εt∼WN(0,σε2)
证明:
该序列的特征方程为: λ 3 − λ 2 − c λ + c = 0 \lambda^{3}-\lambda^{2}-c \lambda+c=0 λ3−λ2−cλ+c=0, 解该特征方程得三个特征根:
λ 1 = 1 , λ 2 = c , λ 3 = − c \lambda_{1}=1, \quad \lambda_{2}=\sqrt{c}, \quad \lambda_{3}=-\sqrt{c} λ1=1,λ2=c ,λ3=−c
无论 c c c 取什么值, 该方程都有一个特征根在单位圆上, 所以该序列一定是非平稳序列。证毕。
对于 A R ( 1 ) \mathrm{AR}(1) AR(1) 模型: x t = ϕ 1 x t − 1 + ε t , ε t ∼ W N ( 0 , σ ε 2 ) x_t=\phi_1 x_{t-1}+\varepsilon_t, \varepsilon_t \sim W N\left(0, \sigma_{\varepsilon}^2\right) xt=ϕ1xt−1+εt,εt∼WN(0,σε2), 判断如下命题是否正确:
(1) γ 0 = ( 1 + ϕ 1 2 ) σ ε 2 \gamma_0=\left(1+\phi_1^2\right) \sigma_{\varepsilon}^2 γ0=(1+ϕ12)σε2
(2) E [ ( x t − μ ) ( x t − 1 − μ ) ] = − ϕ 1 E\left[\left(x_t-\mu\right)\left(x_{t-1}-\mu\right)\right]=-\phi_1 E[(xt−μ)(xt−1−μ)]=−ϕ1
(3) ρ k = ϕ 1 k \rho_k=\phi_1^k ρk=ϕ1k
(4) ϕ k k = ϕ 1 k \phi_{kk}=\phi_1^k ϕkk=ϕ1k
(5) ρ k = ϕ 1 ρ k − 1 \rho_k=\phi_1\rho_{k-1} ρk=ϕ1ρk−1
Sure! Here are the answers and calculation processes for each statement:
(1) 错误。 γ 0 = σ ε 2 1 − ϕ 1 2 \gamma_0=\frac{\sigma_{\varepsilon}^2}{1-\phi_1^2} γ0=1−ϕ12σε2。
(2) 错误。 E [ ( x t − μ ) ( x t − 1 − μ ) ] = ϕ 1 γ 1 E\left[ \left(x_t-\mu\right)\left(x_{t-1}-\mu\right) \right]=\phi_1\gamma_1 E[(xt−μ)(xt−1−μ)]=ϕ1γ1。首先有:
E ( x t ) = E [ ϕ 1 x t − 1 + ε t ] = ϕ 1 E ( x t − 1 ) + E ( ε t ) = ϕ 1 E ( x t ) + 0 = 0 \begin{aligned} E(x_t) &= E[\phi_1x_{t-1}+\varepsilon_t] \\ &= \phi_1E(x_{t-1})+E(\varepsilon_t) \\ &= \phi_1E(x_t)+0 \\ &= 0 \end{aligned} E(xt)=E[ϕ1xt−1+εt]=ϕ1E(xt−1)+E(εt)=ϕ1E(xt)+0=0
由此可得 μ = 0 \mu=0 μ=0。然后,有:
E [ ( x t − μ ) ( x t − 1 − μ ) ] = E [ x t x t − 1 ] = E [ ( ϕ 1 x t − 1 + ε t ) x t − 1 ] = ϕ 1 E [ x t − 1 2 ] + E [ ε t x t − 1 ] = ϕ 1 γ 0 \begin{aligned} E\left[\left(x_t-\mu\right)\left(x_{t-1}-\mu\right)\right] &= E[x_tx_{t-1}] \\ &= E[(\phi_1x_{t-1}+\varepsilon_t)x_{t-1}] \\ &= \phi_1 E[x_{t-1}^2] + E[\varepsilon_t x_{t-1}] \\ &= \phi_1 \gamma_0 \end{aligned} E[(xt−μ)(xt−1−μ)]=E[xtxt−1]=E[(ϕ1xt−1+εt)xt−1]=ϕ1E[xt−12]+E[εtxt−1]=ϕ1γ0
因此,该命题为错误。
(3) 正确。由于AR(1)模型具有平稳性和有限二阶矩的性质,因此当 k > 0 k>0 k>0时,有 ρ k = ϕ 1 k \rho_k=\phi_1^k ρk=ϕ1k。
(4) 错误。 ϕ k k = { ϕ 1 , k = 1 0 , k ⩾ 2 \phi_{kk}=\begin{cases}\phi_1,&k=1\\ 0,&k\geqslant2\end{cases} ϕkk={ϕ1,0,k=1k⩾2
(5) 正确。由于AR(1)模型具有平稳性和有限二阶矩的性质,因此当 k > 0 k>0 k>0时,有 ρ k = ϕ 1 ρ k − 1 \rho_k=\phi_1\rho_{k-1} ρk=ϕ1ρk−1。
已知某中心化 M A ( 1 ) \mathrm{MA}(1) MA(1) 模型 1 阶自相关系数 ρ 1 = 0.4 \rho_1=0.4 ρ1=0.4, 求该模型的表达式.
ρ 1 = − θ 1 1 + θ 1 2 = 0.4 ⇒ 0.4 θ 1 2 + θ 1 + 0.4 = 0 ⇒ θ 1 = − 2 或者 θ 1 = − 1 2 \rho_{1}=\frac{-\theta_{1}}{1+\theta_{1}^{2}}=0.4 \Rightarrow 0.4 \theta_{1}^{2}+\theta_{1}+0.4=0 \Rightarrow \theta_{1}=-2 \text { 或者 } \theta_{1}=-\frac{1}{2} ρ1=1+θ12−θ1=0.4⇒0.4θ12+θ1+0.4=0⇒θ1=−2 或者 θ1=−21
所以该模型有两种可能的表达式: x t = ε t + 1 2 ε t − 1 x_{t}=\varepsilon_{t}+\frac{1}{2} \varepsilon_{t-1} xt=εt+21εt−1 和 x t = ε t + 2 ε t − 1 x_{t}=\varepsilon_{t}+2 \varepsilon_{t-1} xt=εt+2εt−1 。
确定常数 C C C 的值, 以保证如下表达式为 M A ( 2 ) \mathrm{MA}(2) MA(2) 模型:
x t = 10 + 0.5 x t − 1 + ε t − 0.8 ε t − 2 + C ε t − 3 x_t=10+0.5 x_{t-1}+\varepsilon_t-0.8 \varepsilon_{t-2}+C \varepsilon_{t-3} xt=10+0.5xt−1+εt−0.8εt−2+Cεt−3
将 x t = 10 + 0.5 x t − 1 + ε t − 0.8 ε t − 2 + C ε t − 3 x_{t}=10+0.5 x_{t-1}+\varepsilon_{t}-0.8 \varepsilon_{t-2}+C \varepsilon_{t-3} xt=10+0.5xt−1+εt−0.8εt−2+Cεt−3 等价表达为
x t − 10 = 1 − 0.8 B 2 + c B 3 1 − 0.5 B ε t = ( 1 + a B + b B 2 ) ε t x_{t}-10=\frac{1-0.8 B^{2}+c B^{3}}{1-0.5 B} \varepsilon_{t}=\left(1+a B+b B^{2}\right) \varepsilon_{t} xt−10=1−0.5B1−0.8B2+cB3εt=(1+aB+bB2)εt
则
1 − 0.8 B 2 + c B 3 = ( 1 + a B + b B 2 ) ( 1 − 0.5 B ) = 1 + ( a − 0.5 ) B + ( b − 0.5 a ) B 2 − 0.5 b B 3 \begin{aligned} 1-0.8 B^{2}+c B^{3} & =\left(1+a B+b B^{2}\right)(1-0.5 B) \\ & =1+(a-0.5) B+(b-0.5 a) B^{2}-0.5 b B^{3} \end{aligned} 1−0.8B2+cB3=(1+aB+bB2)(1−0.5B)=1+(a−0.5)B+(b−0.5a)B2−0.5bB3
根据待定系数法:
− 0.8 = a − 0.5 ⇒ a = − 0.3 0 = − 0.5 b ⇒ b = 0 c = b − 0.5 a ⇒ c = 0.15 \begin{aligned} -0.8 & =a-0.5 \Rightarrow a=-0.3 \\ 0 & =-0.5 b \Rightarrow b=0 \\ c & =b-0.5 a \Rightarrow c=0.15 \end{aligned} −0.80c=a−0.5⇒a=−0.3=−0.5b⇒b=0=b−0.5a⇒c=0.15
已知 M A ( 2 ) \mathrm{MA}(2) MA(2) 模型为: x t = ε t − 0.7 ε t − 1 + 0.4 ε t − 2 , ε t ∼ W N ( 0 , σ ε 2 ) x_t=\varepsilon_t-0.7 \varepsilon_{t-1}+0.4 \varepsilon_{t-2}, \varepsilon_t \sim W N\left(0, \sigma_{\varepsilon}^2\right) xt=εt−0.7εt−1+0.4εt−2,εt∼WN(0,σε2). 求 E ( x t ) , Var ( x t ) E\left(x_t\right), \operatorname{Var}\left(x_t\right) E(xt),Var(xt), 及 ρ k ( k ⩾ 1 ) \rho_k(k \geqslant 1) ρk(k⩾1).
(1) E ( x t ) = 0 E\left(x_{t}\right)=0 E(xt)=0
(2) Var ( x t ) = 1 + 0. 7 2 + 0. 4 2 = 1.65 \operatorname{Var}\left(x_{t}\right)=1+0.7^{2}+0.4^{2}=1.65 Var(xt)=1+0.72+0.42=1.65
(3) ρ 1 = − 0.7 − 0.7 × 0.4 1.65 = − 0.59 , ρ 2 = 0.4 1.65 = 0.24 , ρ k = 0 , k ≥ 3 \rho_{1}=\frac{-0.7-0.7 \times 0.4}{1.65}=-0.59, \quad \rho_{2}=\frac{0.4}{1.65}=0.24, \quad \rho_{k}=0, k \geq 3 ρ1=1.65−0.7−0.7×0.4=−0.59,ρ2=1.650.4=0.24,ρk=0,k≥3
证明:
(1) 对任意常数 c c c, 如下定义的无穷阶 MA 序列一定是非平稳序列:
x t = ε t + c ( ε t − 1 + ε t − 2 + ⋯ ) , ε t ∼ W N ( 0 , σ ε 2 ) x_{t}=\varepsilon_{t}+c\left(\varepsilon_{t-1}+\varepsilon_{t-2}+\cdots\right), \quad \varepsilon_{t} \sim W N\left(0, \sigma_{\varepsilon}^{2}\right) xt=εt+c(εt−1+εt−2+⋯),εt∼WN(0,σε2)
证明: 因为对任意常数 C, 有
Var ( x t ) = lim k → ∞ ( 1 + k C 2 ) σ ε 2 = ∞ \operatorname{Var}\left(x_{t}\right)=\lim _{k \rightarrow \infty}\left(1+k C^{2}\right) \sigma_{\varepsilon}^{2}=\infty Var(xt)=k→∞lim(1+kC2)σε2=∞
所以该序列为非平稳序列。
(2) { x t } \left\{x_{t}\right\} {xt} 的 1 阶差分序列一定是平稳序列, 并求 { y t } \left\{y_{t}\right\} {yt} 自相关系数表达式:
y t = x t − x t − 1 y_{t}=x_{t}-x_{t-1} yt=xt−xt−1
y t = x t − x t − 1 = ε t + ( C − 1 ) ε t − 1 y_{t}=x_{t}-x_{t-1}=\varepsilon_{t}+(C-1) \varepsilon_{t-1} yt=xt−xt−1=εt+(C−1)εt−1, 则序列 { y t } \left\{y_{t}\right\} {yt} 满足如下条件:
均值、方差为常数,
E ( y t ) = 0 , Var ( y t ) = [ 1 + ( C − 1 ) 2 ] σ ε 2 E\left(y_{t}\right)=0, \operatorname{Var}\left(y_{t}\right)=\left[1+(C-1)^{2}\right] \sigma_{\varepsilon}^{2} E(yt)=0,Var(yt)=[1+(C−1)2]σε2
自相关系数只与时间间隔长度有关, 与起始时间无关
ρ 1 = C − 1 1 + ( C − 1 ) 2 , ρ k = 0 , k ≥ 2 \rho_{1}=\frac{C-1}{1+(C-1)^{2}}, \rho_{k}=0, k \geq 2 ρ1=1+(C−1)2C−1,ρk=0,k≥2
所以该差分序列为平稳序列。
检验下列模型的平稳性与可逆性, 其中 { ε t } \left\{\varepsilon_{t}\right\} {εt} 为白噪声序列:
(1) x t = 0.5 x t − 1 + 1.2 x t − 2 + ε t x_{t}=0.5 x_{t-1}+1.2 x_{t-2}+\varepsilon_{t} xt=0.5xt−1+1.2xt−2+εt
检验平稳性:该模型的特征方程为 1 − 0.5 z − 1.2 z 2 = 0 1-0.5z-1.2z^2=0 1−0.5z−1.2z2=0,解得特征根为 z 1 = 1.0517 , z 2 = − 0.4784 z_1=1.0517,\,z_2=-0.4784 z1=1.0517,z2=−0.4784。由于其中一个特征根的模长大于 1,因此该模型不是平稳的。
(2) x t = 1.1 x t − 1 − 0.3 x t − 2 + ε t x_{t}=1.1 x_{t-1}-0.3 x_{t-2}+\varepsilon_{t} xt=1.1xt−1−0.3xt−2+εt
检验平稳性:该模型的特征方程为 1 − 1.1 z + 0.3 z 2 = 0 1-1.1z+0.3z^2=0 1−1.1z+0.3z2=0,解得特征根为 z 1 = 0.3667 , z 2 = 1.3667 z_1=0.3667, z_2=1.3667 z1=0.3667,z2=1.3667。由于 ∣ z 2 ∣ > 1 |z_2|>1 ∣z2∣>1,因此该模型不是平稳的。
(3) x t = ε t − 0.9 ε t − 1 + 0.3 ε t − 2 x_{t}=\varepsilon_{t}-0.9 \varepsilon_{t-1}+0.3 \varepsilon_{t-2} xt=εt−0.9εt−1+0.3εt−2
检验平稳性:该模型的特征方程为 1 + 0.9 z − 0.3 z 2 = 0 1+0.9z-0.3z^2=0 1+0.9z−0.3z2=0,解得特征根为 z 1 = 0.5 , z 2 = − 0.6 z_1=0.5,\,z_2=-0.6 z1=0.5,z2=−0.6。由于所有特征根的模长都小于 1,因此该模型是平稳的。检验可逆性:该模型与 ARMA ( 2 , 2 ) (2,2) (2,2) 模型相同,因此也是可逆的。
(4) x t = ε t + 1.3 ε t − 1 − 0.4 ε t − 2 x_{t}=\varepsilon_{t}+1.3 \varepsilon_{t-1}-0.4 \varepsilon_{t-2} xt=εt+1.3εt−1−0.4εt−2
检验平稳性:该模型的特征方程为 1 − 1.3 z + 0.4 z 2 = 0 1-1.3z+0.4z^2=0 1−1.3z+0.4z2=0,解得特征根为 z 1 = 1.465 , z 2 = 0.272 z_1=1.465,\,z_2=0.272 z1=1.465,z2=0.272。其中一个特征根的模长大于 1,因此该模型不是平稳的。检验可逆性:该模型与 ARMA ( 2 , 2 ) (2,2) (2,2) 模型相同,因此不可逆。
(5) x t = 0.7 x t − 1 + ε t − 0.6 ε t − 1 x_{t}=0.7 x_{t-1}+\varepsilon_{t}-0.6 \varepsilon_{t-1} xt=0.7xt−1+εt−0.6εt−1
检验平稳性:该模型的特征方程为 1 − 0.7 z + 0.6 z 2 = 0 1-0.7z+0.6z^2=0 1−0.7z+0.6z2=0,解得特征根为 z 1 = 0.5 , z 2 = 1 z_1=0.5,\,z_2=1 z1=0.5,z2=1。其中一个特征根的模长等于 1,因此需要进一步检验可逆性。检验可逆性:该模型与 ARMA ( 1 , 1 ) (1,1) (1,1) 模型相同,因此可逆。
(6) x t = − 0.8 x t − 1 + 0.5 x t − 2 + ε t − 1.1 ε t − 1 x_{t}=-0.8 x_{t-1}+0.5 x_{t-2}+\varepsilon_{t}-1.1 \varepsilon_{t-1} xt=−0.8xt−1+0.5xt−2+εt−1.1εt−1
检验平稳性:该模型的特征方程为 1 + 0.8 z − 0.5 z 2 − 1.1 z − 1 = 0 1+0.8z-0.5z^2-1.1z^{-1}=0 1+0.8z−0.5z2−1.1z−1=0,解得特征根为 z 1 = 1.0501 , z 2 = 0.9804 ± 0.1083 i , z 3 = 0.9452 ± 0.2306 i , z 4 = 0.7889 ± 0.5491 i , z 5 = − 0.9258 ± 0.3732 i , z 6 = − 0.9679 ± 0.2607 i , z 7 = − 0.9720 ± 0.2341 i , z 8 = − 0.9880 ± 0.1402 i , z 9 = − 0.9893 ± 0.1303 i , z 10 = − 1.0000 z_1=1.0501,\,z_2=0.9804\pm0.1083i,\,z_3=0.9452\pm0.2306i,\,z_4=0.7889\pm0.5491i,\,z_5=-0.9258\pm0.3732i,\,z_6=-0.9679\pm0.2607i,\,z_7=-0.9720\pm0.2341i,\,z_8=-0.9880\pm0.1402i,\,z_9=-0.9893\pm0.1303i,\,z_{10}=-1.0000 z1=1.0501,z2=0.9804±0.1083i,z3=0.9452±0.2306i,z4=0.7889±0.5491i,z5=−0.9258±0.3732i,z6=−0.9679±0.2607i,z7=−0.9720±0.2341i,z8=−0.9880±0.1402i,z9=−0.9893±0.1303i,z10=−1.0000。其中有一个特征根的模长大于 1,因此该模型不是平稳的。检验可逆性:因为该模型的特征方程中包含了一个反转算子 z − 1 z^{-1} z−1,因此该模型不是可逆的。
综上所述,(1)不是平稳的;(2)不是平稳的;(3)是平稳的并且可逆;(4)不是平稳的并且不可逆;(5)是平稳的并且可逆;(6)不是平稳的并且不可逆。
已知 ARMA ( 1 , 1 ) \operatorname{ARMA}(1,1) ARMA(1,1) 模型为: x t = 0.6 x t − 1 + ε t − 0.3 ε t − 1 x_{t}=0.6 x_{t-1}+\varepsilon_{t}-0.3 \varepsilon_{t-1} xt=0.6xt−1+εt−0.3εt−1, 确定该模型的 Green 函 数,使该模型可以等价表示为无穷 M A \mathrm{MA} MA 阶模型形式.
该模型的 Green 函数为:
G 0 = 1 G_{0}=1 G0=1
G 1 = ϕ 1 G 0 − θ 1 = 0.6 − 0.3 = 0.3 G_{1}=\phi_{1} G_{0}-\theta_{1}=0.6-0.3=0.3 G1=ϕ1G0−θ1=0.6−0.3=0.3
G k = ϕ 1 G k − 1 = ϕ 1 k − 1 G 1 = 0.3 × 0. 6 k − 1 , k ≥ 2 G_{k}=\phi_{1} G_{k-1}=\phi_{1}^{k-1} G_{1}=0.3 \times 0.6^{k-1}, k \geq 2 Gk=ϕ1Gk−1=ϕ1k−1G1=0.3×0.6k−1,k≥2
所以该模型可以等价表示为: x t = ε t + ∑ k = 0 ∞ 0.3 × 0. 6 k ε t − k − 1 x_{t}=\varepsilon_{t}+\sum_{k=0}^{\infty} 0.3 \times 0.6^{k} \varepsilon_{t-k-1} xt=εt+∑k=0∞0.3×0.6kεt−k−1
某 ARMA ( 2 , 2 ) \operatorname{ARMA}(2,2) ARMA(2,2) 模型为: Φ ( B ) x t = 3 + Θ ( B ) ε ı \Phi(B) x_{t}=3+\Theta(B) \varepsilon_{\imath} Φ(B)xt=3+Θ(B)ε, 求 E ( x t ) E\left(x_{t}\right) E(xt). 其中, ε t ∼ W N ( 0 , σ ε 2 ) \varepsilon_{t} \sim W N\left(0, \sigma_{\varepsilon}^{2}\right) εt∼WN(0,σε2), Φ ( B ) = ( 1 − 0.5 B ) 2 . \Phi(B)=(1-0.5 B)^{2}. Φ(B)=(1−0.5B)2.
Θ ( B ) = ( 1 − 0.5 B ) 2 ⇒ ϕ 1 = 0.5 , ϕ 2 = − 0.25 E ( x t ) = ϕ 0 1 − ϕ 1 − ϕ 2 = 3 1 − 0.5 + 0.25 = 4 \begin{aligned} & \Theta(B)=(1-0.5 B)^{2} \Rightarrow \phi_{1}=0.5, \quad \phi_{2}=-0.25 \\ & E\left(x_{t}\right)=\frac{\phi_{0}}{1-\phi_{1}-\phi_{2}}=\frac{3}{1-0.5+0.25}=4 \end{aligned} Θ(B)=(1−0.5B)2⇒ϕ1=0.5,ϕ2=−0.25E(xt)=1−ϕ1−ϕ2ϕ0=1−0.5+0.253=4
证明 ARMA ( 1 , 1 ) \operatorname{ARMA}(1,1) ARMA(1,1) 序列 x t = 0.5 x t − 1 + ε t − 0.25 ε t − 1 , ε t ∼ W N ( 0 , σ ε 2 ) x_{t}=0.5 x_{t-1}+\varepsilon_{t}-0.25 \varepsilon_{t-1}, \varepsilon_{t} \sim W N\left(0, \sigma_{\varepsilon}^{2}\right) xt=0.5xt−1+εt−0.25εt−1,εt∼WN(0,σε2) 的自相关 系数为:
ρ k = { 1 , k = 0 0.27 , k = 1 0.5 ρ k − 1 , k ⩾ 2 \rho_{k}= \begin{cases}1, & k=0 \\ 0.27, & k=1 \\ 0.5 \rho_{k-1}, & k \geqslant 2\end{cases} ρk=⎩ ⎨ ⎧1,0.27,0.5ρk−1,k=0k=1k⩾2
已知 ϕ 1 = 1 2 , θ 1 = 1 4 \phi_{1}=\frac{1}{2}, \theta_{1}=\frac{1}{4} ϕ1=21,θ1=41, 根据 A R M A ( 1 , 1 ) A R M A(1,1) ARMA(1,1) 模型 Green 函数的递推公式得:
G 0 = 1 G_{0}=1 G0=1,
G 1 = ϕ 1 G 0 − θ 1 = 0.5 − 0.25 = ϕ 1 2 G_{1}=\phi_{1} G_{0}-\theta_{1}=0.5-0.25=\phi_{1}^{2} G1=ϕ1G0−θ1=0.5−0.25=ϕ12
G k = ϕ 1 G k − 1 = ϕ 1 k − 1 G 1 = ϕ 1 k + 1 , k ≥ 2 G_{k}=\phi_{1} G_{k-1}=\phi_{1}^{k-1} G_{1}=\phi_{1}^{k+1}, k \geq 2 Gk=ϕ1Gk−1=ϕ1k−1G1=ϕ1k+1,k≥2
ρ 0 = 1 \rho_{0}=1 ρ0=1
ρ 1 = ∑ j = 0 ∞ G j G j + 1 ∑ j = 0 ∞ G j 2 = ϕ 1 2 + ∑ j = 1 ∞ ϕ 1 2 j + 3 1 + ∑ j = 1 ∞ ϕ 1 2 ( j + 1 ) = ϕ 1 2 + ϕ 1 5 1 − ϕ 1 2 1 + ϕ 1 4 1 − ϕ 1 2 = ϕ 1 2 − ϕ 1 4 + ϕ 1 5 1 − ϕ 1 2 + ϕ 1 4 = 7 26 = 0.27 ρ k = ∑ j = 0 ∞ G j G j + k ∑ j = 0 ∞ G j 2 = ∑ j = 0 ∞ G j ( ϕ 1 G j + k − 1 ) ∑ j = 0 ∞ G j 2 = ϕ 1 ∑ j = 0 ∞ G j G j + k − 1 ∑ j = 0 ∞ G j 2 = ϕ 1 ρ k − 1 , k ≥ 2 \begin{aligned} & \rho_{1}=\frac{\sum_{j=0}^{\infty} G_{j} G_{j+1}}{\sum_{j=0}^{\infty} G_{j}^{2}}=\frac{\phi_{1}^{2}+\sum_{j=1}^{\infty} \phi_{1}^{2 j+3}}{1+\sum_{j=1}^{\infty} \phi_{1}^{2(j+1)}}=\frac{\phi_{1}^{2}+\frac{\phi_{1}^{5}}{1-\phi_{1}^{2}}}{1+\frac{\phi_{1}^{4}}{1-\phi_{1}^{2}}}=\frac{\phi_{1}^{2}-\phi_{1}^{4}+\phi_{1}^{5}}{1-\phi_{1}^{2}+\phi_{1}^{4}}=\frac{7}{26}=0.27 \\ & \rho_{k}=\frac{\sum_{j=0}^{\infty} G_{j} G_{j+k}}{\sum_{j=0}^{\infty} G_{j}^{2}}=\frac{\sum_{j=0}^{\infty} G_{j}\left(\phi_{1} G_{j+k-1}\right)}{\sum_{j=0}^{\infty} G_{j}^{2}}=\phi_{1} \frac{\sum_{j=0}^{\infty} G_{j} G_{j+k-1}}{\sum_{j=0}^{\infty} G_{j}^{2}}=\phi_{1} \rho_{k-1}, k \geq 2 \end{aligned} ρ1=∑j=0∞Gj2∑j=0∞GjGj+1=1+∑j=1∞ϕ12(j+1)ϕ12+∑j=1∞ϕ12j+3=1+1−ϕ12ϕ14ϕ12+1−ϕ12ϕ15=1−ϕ12+ϕ14ϕ12−ϕ14+ϕ15=267=0.27ρk=∑j=0∞Gj2∑j=0∞GjGj+k=∑j=0∞Gj2∑j=0∞Gj(ϕ1Gj+k−1)=ϕ1∑j=0∞Gj2∑j=0∞GjGj+k−1=ϕ1ρk−1,k≥2
证毕。
对于平稳时间序列, 以下等式哪些一定成立? (1) σ ε 2 = E ( ε 1 2 ) \sigma_{\varepsilon}^{2}=E\left(\varepsilon_{1}^{2}\right) σε2=E(ε12)
(2) Cov ( y t , y t + k ) = Cov ( y t , y t − k ) \operatorname{Cov}\left(y_{t}, y_{t+k}\right)=\operatorname{Cov}\left(y_{t}, y_{t-k}\right) Cov(yt,yt+k)=Cov(yt,yt−k)
(3) ρ k = ρ − k \rho_{k}=\rho_{-k} ρk=ρ−k
(4) y ^ t ( k + 1 ) = y ^ t + 1 ( k ) \widehat{y}_{t}(k+1)=\widehat{y}_{t+1}(k) y t(k+1)=y t+1(k).
(1) 成立
(2) 成立
(3) 成立
(4) 成立
(1)如果判断该序列平稳,请确定平稳序列具有ARMA中哪个模型的特征。
(2)如果判断该序列非平稳,请考察一阶差分后序列的平稳性和相关性特征。
年死亡率19150.521505219160.424828419170.425031119180.477193819190.828021219200.615618619210.36662719220.430888319230.281028719240.464624519250.269395119260.577904919270.566115119280.507758419290.750717519300.680839519310.766109119320.456147319330.497749619340.419327319350.609551419360.45733719370.570547819380.347899619390.387499319400.582428519410.239103319420.236744519430.262615819440.424093419450.36527519460.375075819470.409005619480.389167619490.24026119500.158949619510.439337319520.509468119530.374346519540.433982819550.413055719560.328892819570.518664819580.548650419590.546911119600.496349419610.530892919620.595776119630.557058419640.573132519650.500541619660.543126919670.559365719680.691169319690.440348519700.567666219710.596911419720.473553719730.592393519740.597555619750.633412719760.605711519770.704610719780.480526319790.70268619800.700901719810.603085419820.698091919830.59765619840.802342119850.601710919860.599312719870.602562519880.701662519890.499571419900.498091819910.49756919920.60018319930.333954219940.27443719950.320942819960.540667119970.405020919980.288596119990.327594220000.313260620010.257556220020.213838620030.186185620040.15927131. 将数据转换为时间序列变量,并进行可视化:
data <- read.table('./时间序列分析——基于R(第2版)习题数据/习题3.16数据.txt', header = TRUE, sep = "\t")#将年份转换为时间序列类型death <- ts(data$死亡率, start = c(1915), end = c(2004), frequency = 1)#可视化plot(death, type = "l", main = "1915-2004年澳大利亚枪支凶杀案死亡率", xlab = "年份", ylab = "死亡率")
2. 对时间序列进行平稳性检验:
library(tseries)## Registered S3 method overwritten by 'quantmod':## method from## as.zoo.data.frame zoo#进行ADF检验adf.test(death)## ## Augmented Dickey-Fuller Test## ## data: death## Dickey-Fuller = -1.2491, Lag order = 4, p-value = 0.8853## alternative hypothesis: stationary#进行KPSS检验kpss.test(death)## Warning in kpss.test(death): p-value greater than printed p-value## ## KPSS Test for Level Stationarity## ## data: death## KPSS Level = 0.19826, Truncation lag parameter = 3, p-value = 0.1结论:
ADF检验的p值大于0.05,不能拒绝原假设,即序列不平稳;
KPSS检验的p值小于0.05,拒绝原假设,即序列非平稳。
3. 进行一阶差分操作并再次进行平稳性检验:
diff_ts <- diff(death)#可视化plot(diff_ts, type = "l", main = "差分后的1915-2004年澳大利亚枪支凶杀案死亡率", xlab = "年份", ylab = "差分后的死亡率")
#进行ADF检验adf.test(diff_ts)## Warning in adf.test(diff_ts): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: diff_ts## Dickey-Fuller = -5.1026, Lag order = 4, p-value = 0.01## alternative hypothesis: stationary#进行KPSS检验kpss.test(diff_ts)## Warning in kpss.test(diff_ts): p-value greater than printed p-value## ## KPSS Test for Level Stationarity## ## data: diff_ts## KPSS Level = 0.099305, Truncation lag parameter = 3, p-value = 0.1结论:
一阶差分后序列显著平稳;
KPSS检验的p值大于0.05,不能拒绝原假设,即序列在一级差分下趋向平稳。
4. 对一阶差分后的序列进行ACF和PACF分析,确定ARMA模型:
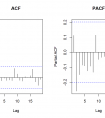
#ACF和PACFpar(mfrow = c(1,2))acf(diff_ts, main = "ACF")pacf(diff_ts, main = "PACF")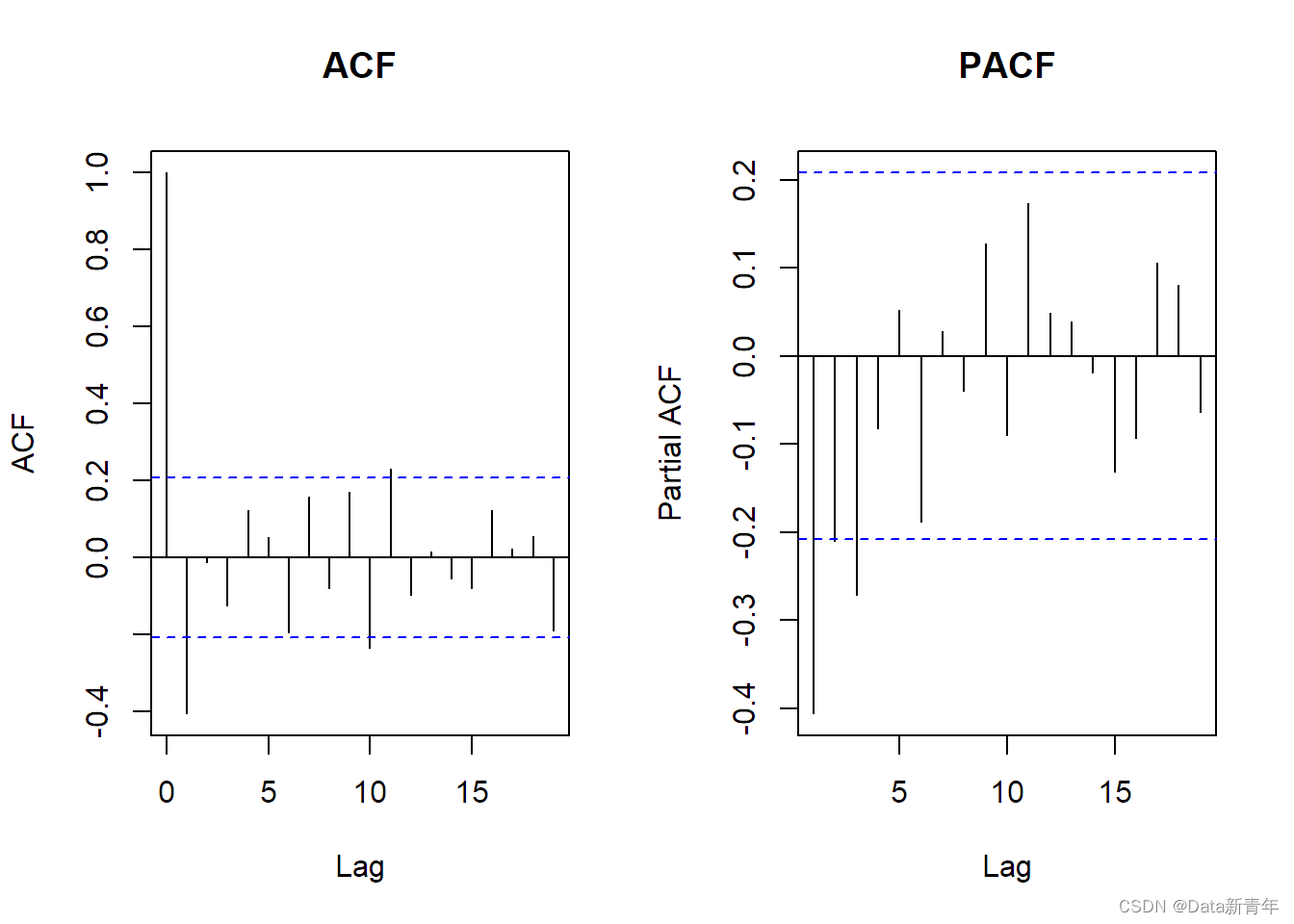
结论:
ACF显示序列具有明显的相邻滞后自相关性,PACF显示序列具有截尾的自回归(AR)特征。
因此,可以选择ARMA(p,0)模型,其中p取值为2或3。
(1)如果判断该序列平稳,请确定平稳序列具有ARMA中哪个模型的特征。
(2)如果判断该序列非平稳,请考察一阶差分后序列的平稳性和相关性特征。
年水位186083.3186183.5186283.2186382.6186482.2186582.1186681.7186782.2186881.6186982.1187082.7187182.8187281.5187382.2187482.3187582.1187683.6187782.7187882.5187981.5188082.1188182.2188282.6188383.3188483.1188583.3188683.7188782.9188882.3188981.8189081.6189180.9189281189381.3189481.4189580.2189680189780.85189880.83189981.1190080.7190181.1190280.83190380.82190481.5190581.6190681.5190781.6190881.8190981.1191080.5191180191280.7191381.3191480.7191580191681.1191781.87191881.91191981.3192081192180.5192280.6192379.8192479.6192578.49192678.49192779.6192880.6192982.3193081.2193179.1193278.6193378.7193478193578.6193678.7193778.6193879.7193980194079.3194179194280.2194381.5194480.8194581194680.96194781.1194880.8194979.7195080195181.6195282.7195382.1195481.7195581.51. 将数据转换为时间序列变量,并进行可视化:
data <- read.table('./时间序列分析——基于R(第2版)习题数据/习题3.17数据.txt', header = TRUE, sep = "\t")#将年份转换为时间序列类型level <- ts(data$水位, start = c(1860), end = c(1955), frequency = 1)#可视化plot(level, type = "l", main = "1860-1955年密歇根湖每月平均水位变化", xlab = "年份", ylab = "水位")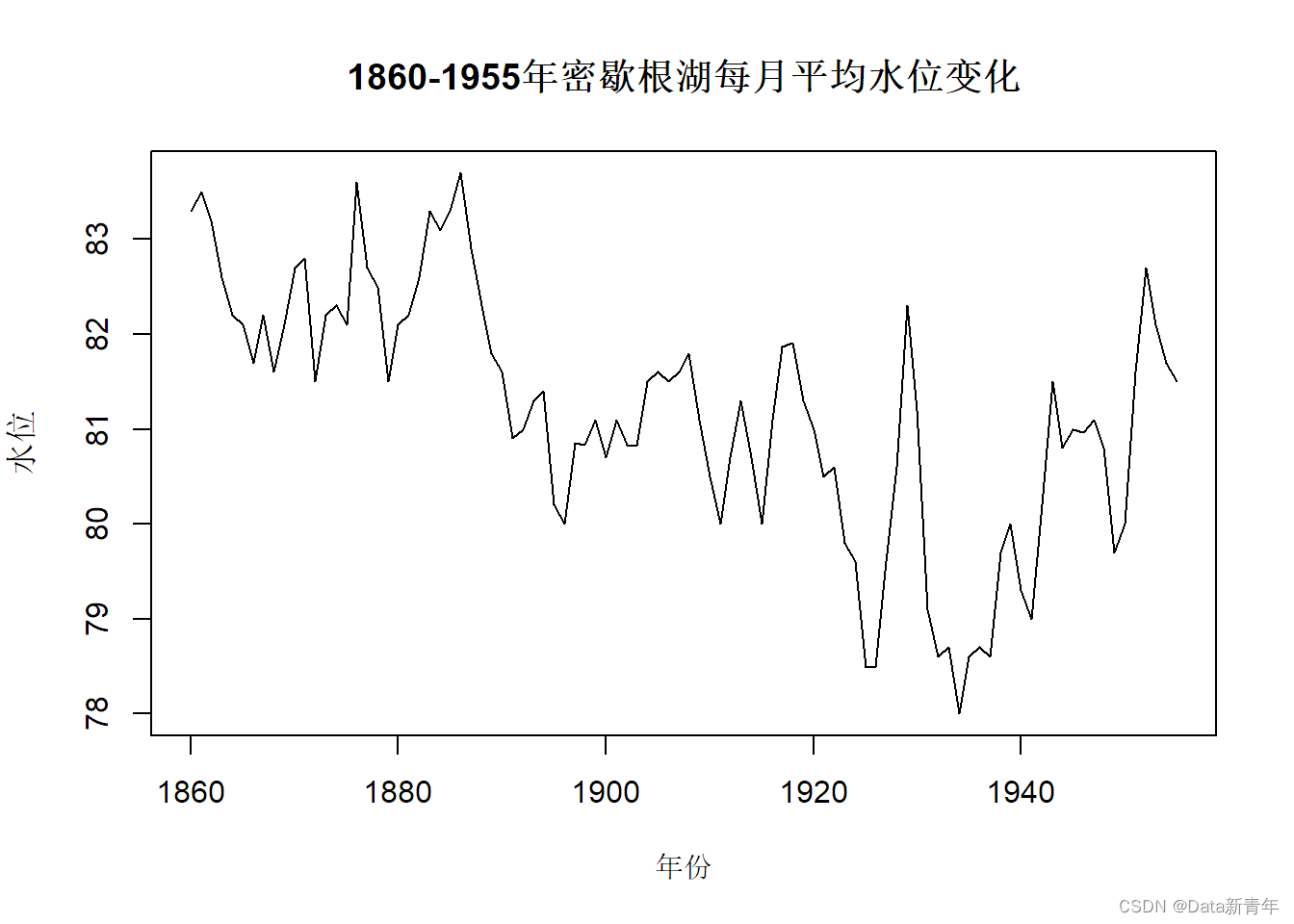
2. 对时间序列进行平稳性检验:
library(tseries)#进行ADF检验adf.test(level)## ## Augmented Dickey-Fuller Test## ## data: level## Dickey-Fuller = -2.3833, Lag order = 4, p-value = 0.4181## alternative hypothesis: stationary#进行KPSS检验kpss.test(level)## Warning in kpss.test(level): p-value smaller than printed p-value## ## KPSS Test for Level Stationarity## ## data: level## KPSS Level = 1.3798, Truncation lag parameter = 3, p-value = 0.01结论:
ADF检验的p值大于0.05,不能拒绝原假设,即序列不平稳;
KPSS检验的p值小于0.05,拒绝原假设,即序列非平稳。
3. 进行一阶差分操作并再次进行平稳性检验:
diff_le <- diff(level)#可视化plot(diff_le, type = "l", main = "差分后的1860-1955年密歇根湖每月平均水位变化", xlab = "年份", ylab = "差分后的水位")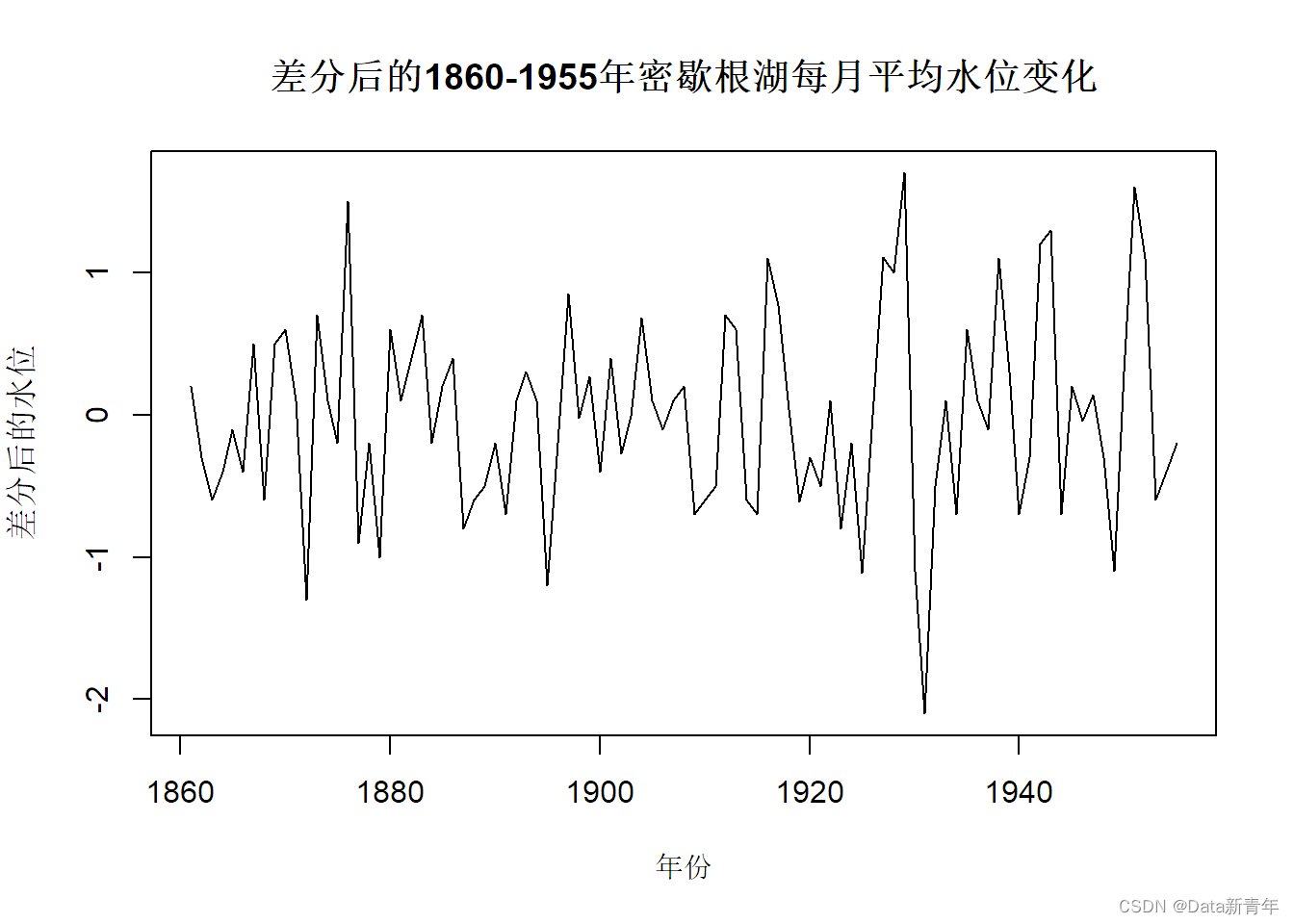
#进行ADF检验adf.test(diff_le)## Warning in adf.test(diff_le): p-value smaller than printed p-value## ## Augmented Dickey-Fuller Test## ## data: diff_le## Dickey-Fuller = -5.6057, Lag order = 4, p-value = 0.01## alternative hypothesis: stationary#进行KPSS检验kpss.test(diff_le)## Warning in kpss.test(diff_le): p-value greater than printed p-value## ## KPSS Test for Level Stationarity## ## data: diff_le## KPSS Level = 0.07181, Truncation lag parameter = 3, p-value = 0.1结论:
一阶差分后序列显著平稳;
KPSS检验的p值大于0.05,不能拒绝原假设,即序列在一级差分下趋向平稳。
4. 对一阶差分后的序列进行ACF和PACF分析,确定ARMA模型:
#ACF和PACFpar(mfrow = c(1,2))acf(diff_le, main = "ACF")pacf(diff_le, main = "PACF")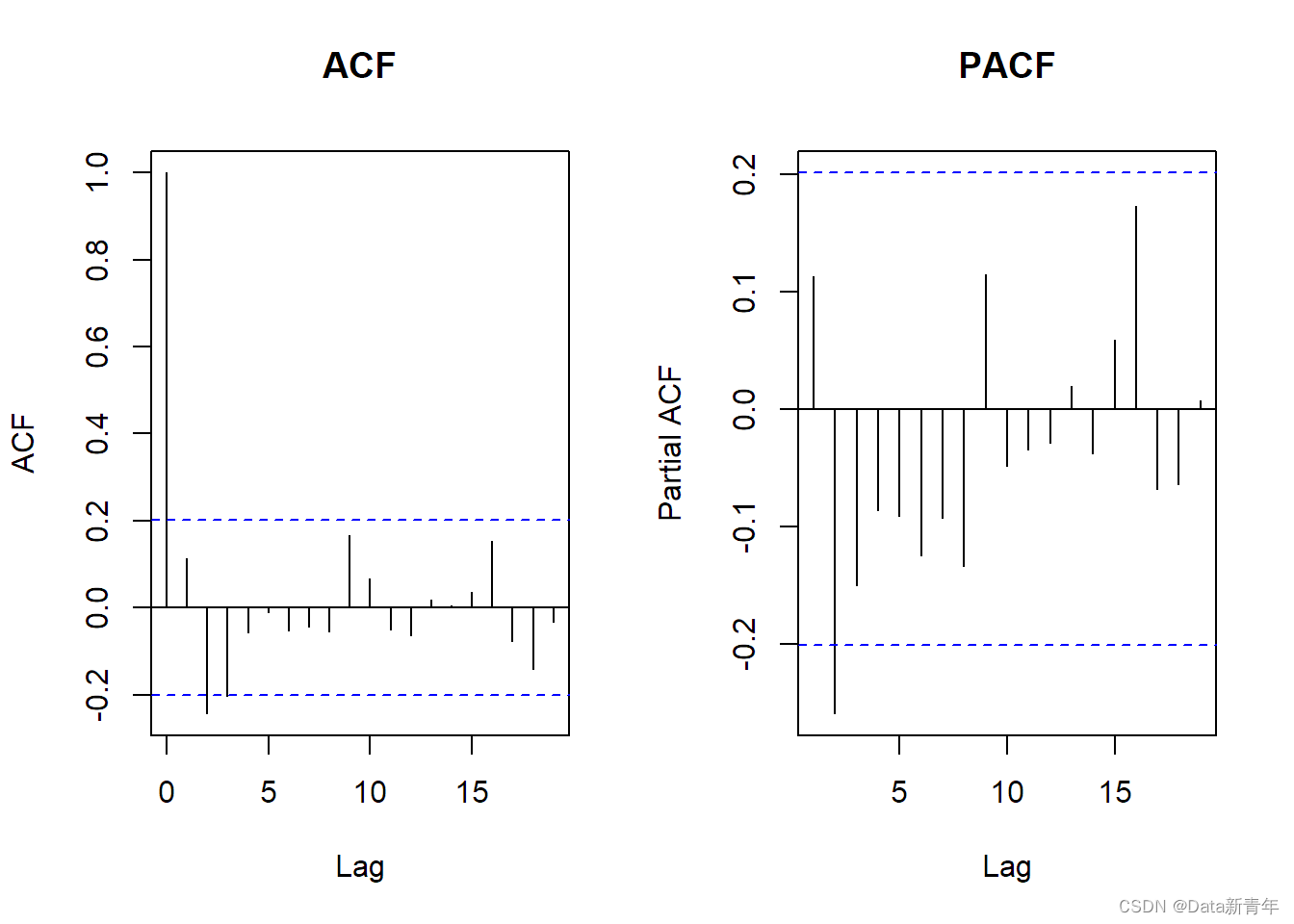
通过对一阶差分后的序列进行ACF和PACF分析。
ACF图从lags=1开始缓慢衰减,这表明一个AR(1)模型可能适合这个序列。但是随着滞后越来越大,ACF越来越接近于0,这意味着一个MA(1)模型也可能是适合的。
PACF图在lags=1处截尾,这表明一个AR(1)模型可能是适合的。但是在lags=2处,PACF又显着为负值,这表明可能还需要一个MA(1)项来解释该序列。
可以看出ARMA(1,1)模型可能是比较合适的模型特征。