一、频域滤波器
1、为什么要进行频率域图像处理?
1) 可以利用频率成分和图像外表之间的对应关系(利用傅里叶变换)。一些在空间域表述困难的增强任务,在频率域中变得非常普通;
2) 图像中的高频分量,指的是图像强度(亮度/灰度)变化剧烈的地方,也就是我们常说的边缘(轮廓);
3)图像中的低频分量,指的是图像强度(亮度/灰度)变换平缓的地方,也就是大片色块的地方。人眼对图像中的高频信号更为敏感。
2、二维离散傅里叶变换
1)定义
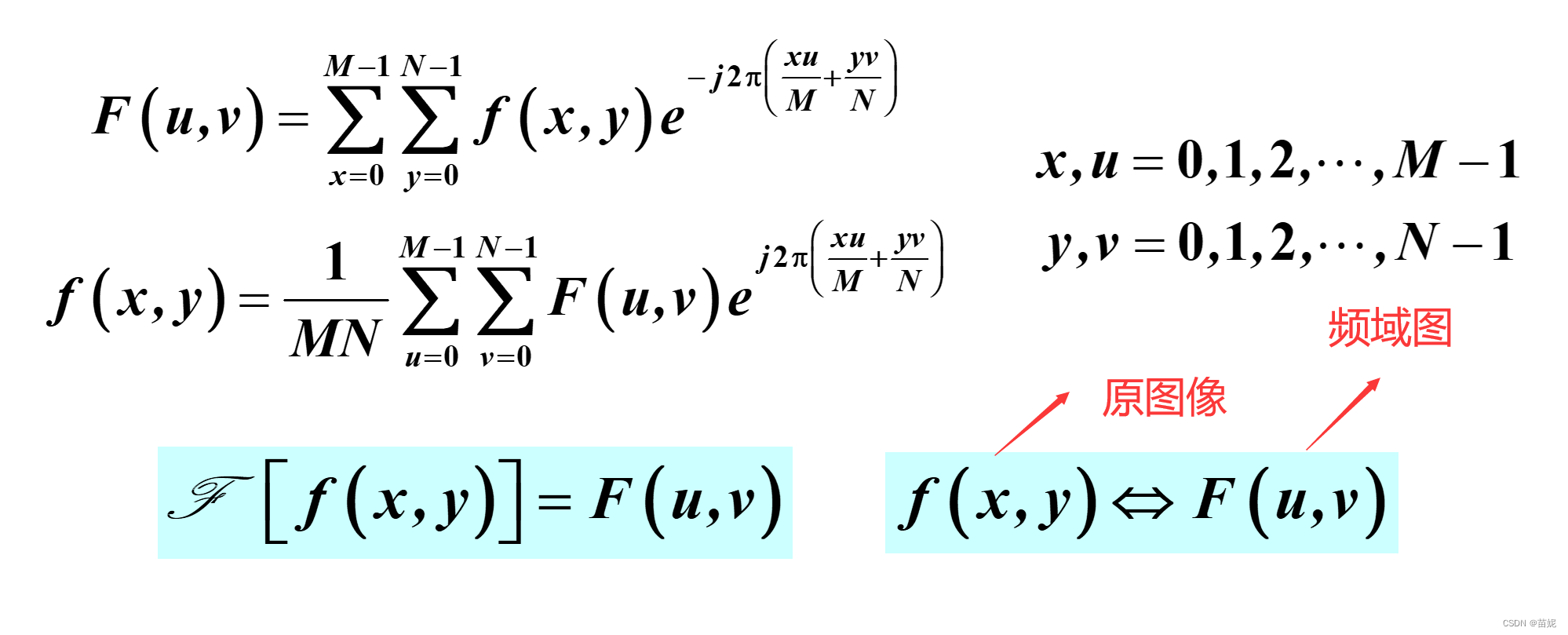
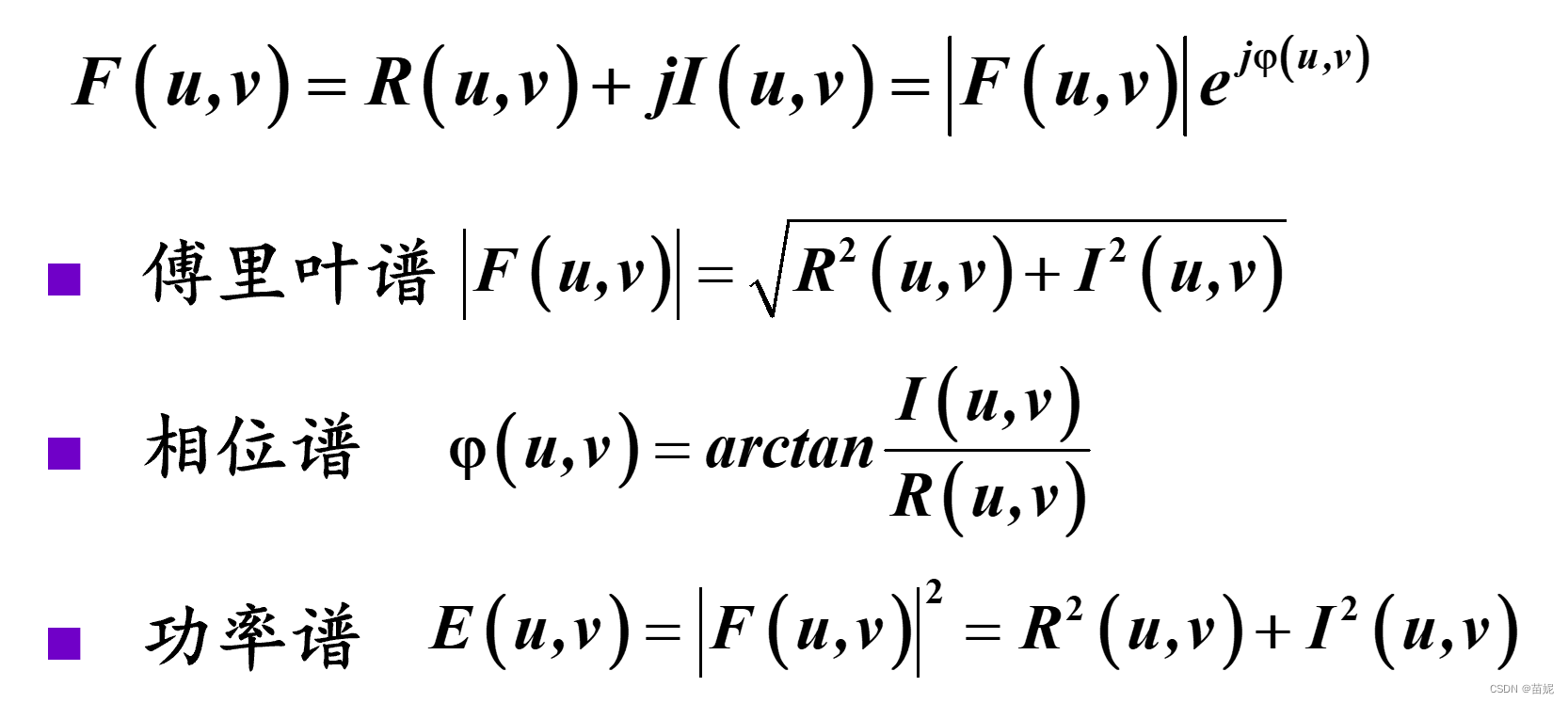
傅里叶变换后的可视化,通常通过功率谱和相位谱来展现。且都有对应的物理意义。傅里叶谱(幅度谱)告诉我们图像中某种频率的成分有多少。低通和高通滤波器实际上是作用于幅度谱。相位谱告诉我们频率成分的具体位置。
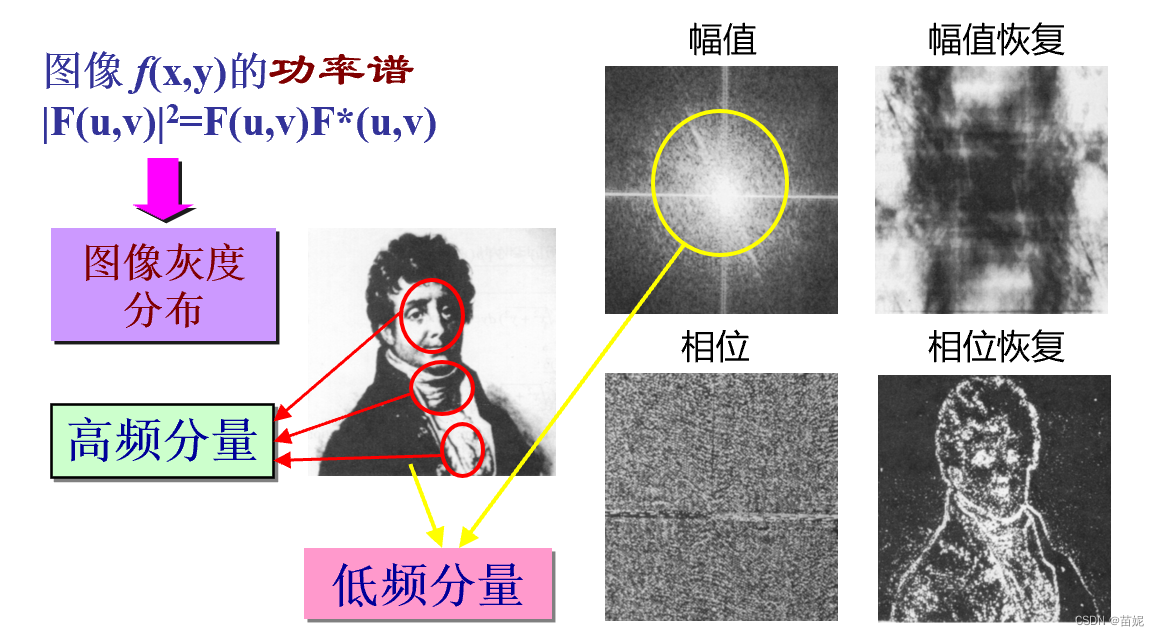
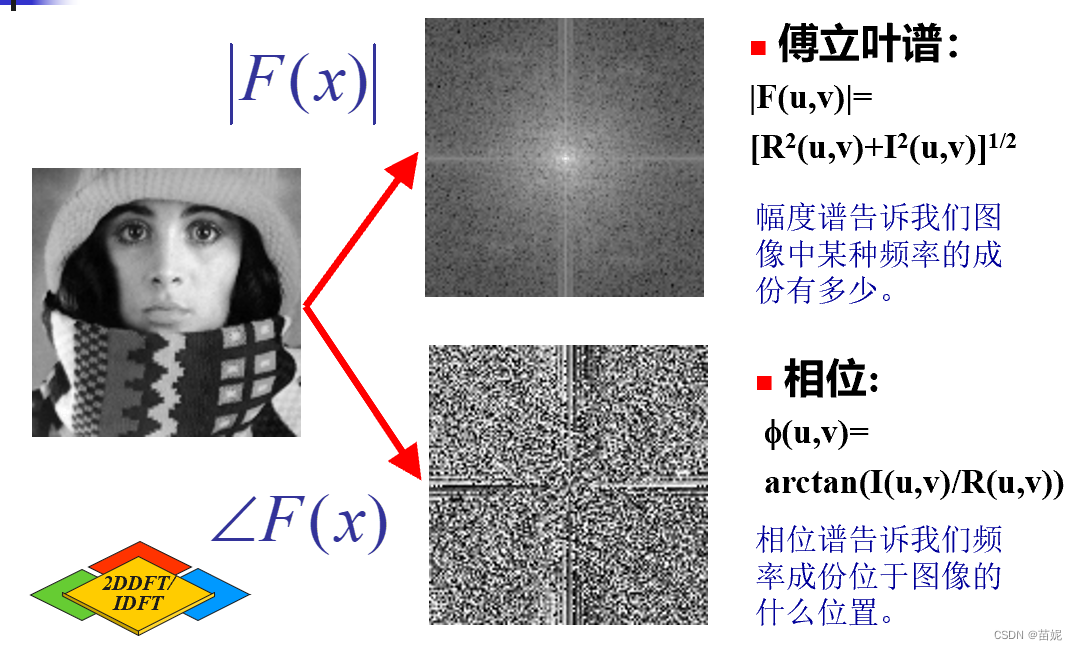
2)二维离散傅里叶变换计算效率怎么样?
二维快速傅里叶变换(2D FFT)是一种用于计算二维数据频域表示的算法,它是对一维快速傅里叶变换(1D FFT)的扩展。与一维情况类似,二维FFT可以在O(N^2logN)的时间复杂度内计算N×N大小的二维数据的离散傅里叶变换。
二维FFT的主要思想是将二维数据分解成一维数据的序列,然后对每一维进行一维FFT变换。这可以通过分别对数据的行和列进行一维FFT来实现。具体步骤如下:
对数据的每一行应用一维FFT。对得到的结果的每一列应用一维FFT。在实际应用中,通常会使用基于分治法的快速傅里叶变换算法(如Cooley-Tukey算法)来实现二维FFT,以提高计算效率。
3、频谱滤波器的步骤
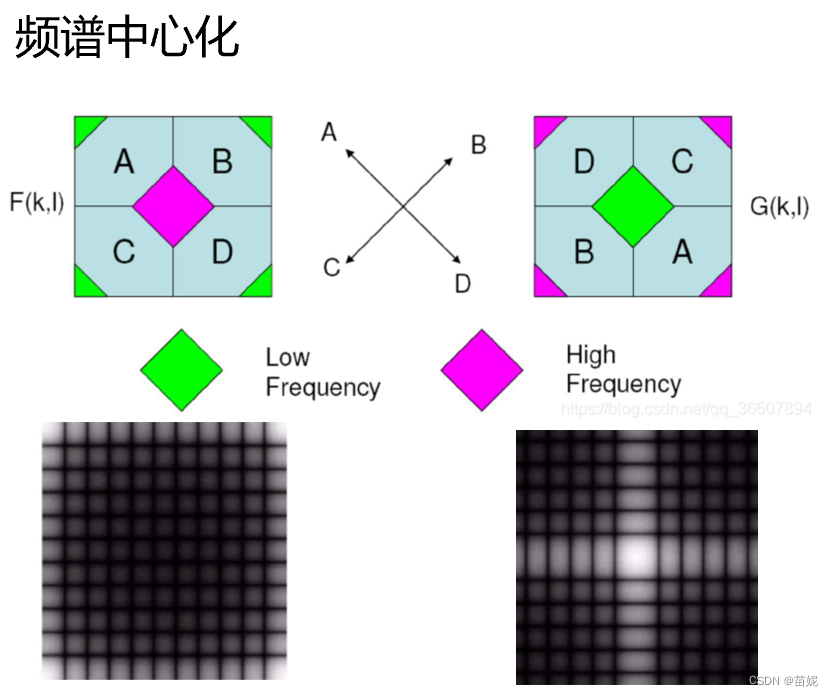
1)用![]() 乘以输入图像进行频谱中心化变换
乘以输入图像进行频谱中心化变换
中心化操作使得频谱的直流分量位于频谱的中心位置,提高了频谱的可读性和解释性,方便信号频率成分的观察和分析。
![]()

2)计算1中的DFT F(u,v)
3)用滤波器函数H(u,v)乘以F(u,v)
4)计算3中结果的反DFT
5)得到4中结果的实部(频谱)
6) 用![]() 乘以5中的结果,取消输入图像的乘数
乘以5中的结果,取消输入图像的乘数
3、高通/低通滤波器
低通 滤波器:使低频通过而使高频衰减的滤波器; 被低通滤波的图像比原始图像少尖锐的细节部分而突出平滑过渡部分; 对比 空间域滤波的平滑处理,如均值滤波器。 高通 滤波器:使高频通过而使低频衰减的滤波器; 被高通滤波的图像比原始图像少灰度级的平滑过渡 而突出边缘等细节部分; 对比 空间域的梯度算子、拉普拉斯算子。
clc,clear;Image=imread('desert.jpg');%读取图像grayIn=rgb2gray(Image);%将彩色图像灰度化[h,w]=size(grayIn);DFTI=fftshift(fft2(grayIn));cf=30;HDFTI=DFTI;HDFTI(h/2-cf:h/2+cf,w/2-cf:w/2+cf)=0;grayOut1=uint8(abs(ifft2(ifftshift(HDFTI))));LDFTI=zeros(h,w);LDFTI(h/2-cf:h/2+cf,w/2-cf:w/2+cf)=DFTI(h/2-cf:h/2+cf,w/2-cf:w/2+cf);grayOut2=uint8(abs(ifft2(ifftshift(LDFTI))));subplot(131),imshow(Image),title('原图');%显示原图像subplot(132),imshow(grayOut1),title('高通滤波');subplot(133),imshow(grayOut2),title('低通滤波');imwrite(grayOut1,'highpass.jpg');imwrite(grayOut2,'lowpass.jpg');二、图像复原
1、应用场景


2、与图像增强的区别

3、图像复原模型
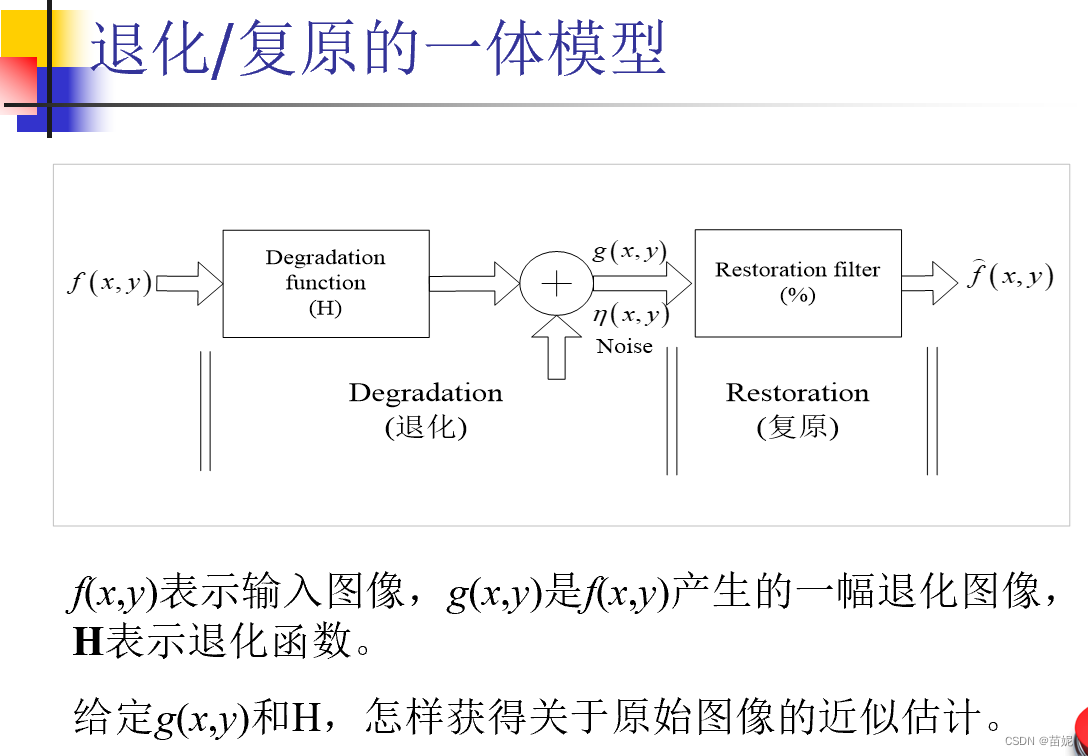
4、代码实现

clear,clc,close all;Image=im2double(rgb2gray(imread('flower.jpg')));subplot(221),imshow(Image),title('Original Image'); LEN=21;THETA=11;PSF=fspecial('motion', LEN, THETA);BlurredI=imfilter(Image, PSF, 'conv', 'circular');noise_mean = 0;noise_var = 0.0001;BlurandnoisyI=imnoise(BlurredI, 'gaussian', noise_mean, noise_var);subplot(222), imshow(BlurandnoisyI),title('Simulate Blur and Noise');imwrite(BlurandnoisyI,'sbn.jpg');estimated_nsr = 0;result1= deconvwnr(BlurandnoisyI, PSF, estimated_nsr);subplot(223),imshow(result1),title('Restoration Using NSR = 0');imwrite(result1,'runsr0.jpg'); estimated_nsr = noise_var / var(Image(:));result2 = deconvwnr(BlurandnoisyI, PSF, estimated_nsr);subplot(224),imshow(result2),title('Restoration Using Estimated NSR');imwrite(result2,'ruensr.jpg');






